Aufgabe 1.1Z: Binäre Entropiefunktion

• Zurück zum Buch

Binäre Entropiefunktion
in „bit” und „nat”

Wir betrachten eine Folge von binären Zufallsgrößen mit dem Symbolvorrat  $\{ \rm A, \ B \}$   ⇒   $M = 2$.  Die Auftrittswahrscheinlichkeiten der beiden Symbole seien  $p_{\rm A }= p$  und  $p_{\rm B } = 1 - p$.

Die einzelnen Folgenelemente sind statistisch unabhängig.  Für die Entropie dieser Nachrichtenquelle gilt gleichermaßen:

$$H_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ld}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ld}\hspace{0.1cm}\frac{1}{1-p}\hspace{0.15cm}{\rm in \hspace{0.15cm} \big [bit \big ]}\hspace{0.05cm},$$

$$H'_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ln}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ln}\hspace{0.1cm}\frac{1}{1-p}\hspace{0.15cm}{\rm in \hspace{0.15cm} \big [nat\big ]}\hspace{0.05cm}.$$

In diesen Gleichungen werden als Kurzbezeichnungen verwendet:

• der natürliche Logarithmus   ⇒   ${\ln} \hspace{0.09cm} p = \log_{\rm e} \hspace{0.05cm} p$,
• der Logarithmus dualis   ⇒   ${\rm ld} \hspace{0.09cm} p = \log_2 \hspace{0.05cm} p$.

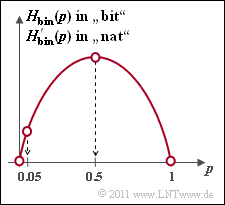
Die Grafik zeigt die binäre Entropiefunktion in Abhängigkeit des Parameters  $p$, wobei  $0 ≤ p ≤ 1$  vorausgesetzt wird.

In den Teilaufgaben  (5)  und  (6)  soll der relative Fehler ermittelt werden, wenn die Symbolwahrscheinlichkeit  $p$  per Simulation  $($also als relative Häufigkeit  $h)$  ermittelt wurde und sich dabei fälschlicherweise  $h = 0.9 \cdot p$  ergeben hat.  Der relative Fehler ist dann wie folgt gegeben:

$$\varepsilon_{H} = \frac{H_{\rm bin}(h)- H_{\rm bin}(p)}{H_{\rm bin}(p)}\hspace{0.05cm}.$$

Hinweis:

• Die Aufgabe gehört zum Kapitel  Gedächtnislose Nachrichtenquellen.

Fragebogen

1

Wie hängen  $H_{\rm bin}(p)$  mit der Einheit „bit” und  $H'_{\rm bin}(p)$  mit der Einheit „nat” zusammen?

	$H_{\rm bin}(p)$  und  $H'_{\rm bin}(p)$  unterscheiden sich um einen Faktor.
	Es gilt  $H'_{\rm bin}(p) = H_{\rm bin}(\ln \ p)$.
	Es gilt  $H'_{\rm bin}(p) = 1 + H_{\rm bin}(2 p)$.

2

Zeigen Sie, dass sich das Maximum der binären Entropiefunktion für  $p = 0.5$  ergibt.  Wie groß ist  $H_\text{bin}(p = 0.5)$?

$H_\text{bin}(p = 0.5) \ = \ $ $\ \rm bit$

3

Berechnen Sie den binären Entropiewert für  $p = 0.05$.

$H_\text{bin}(p = 0.05) \ = \ $ $\ \rm bit$

4

Geben Sie den größeren der beiden  $p$–Werte ein, die sich aus der Gleichung  $H_\text{bin}(p)= 0.5 \ \rm bit$  ergeben.

$p \ = \ $

5

Durch unzureichende Simulation wurde  $p = 0.5$  um  $10\%$ zu niedrig ermittelt.  Wie groß ist der prozentuale Fehler hinsichtlich der Entropie?

$p = 0.45\ \ {\rm statt}\ \ p=0.5\hspace{-0.1cm}:\ \ \varepsilon_H \ = \ $ $\ \rm \%$

6

Durch unzureichende Simulation wurde  $p = 0.05$  um  $10\%$  zu niedrig ermittelt.  Wie groß ist hier der prozentuale Fehler hinsichtlich der Entropie?

$p = 0.045\ \ {\rm statt}\ \ p=0.05\hspace{-0.1cm}:\ \ \varepsilon_H \ = \ $ $\ \rm \%$

Musterlösung

Musterlösung

(1)  Richtig ist der erste Lösungsvorschlag. Die beiden weiteren Vorgaben machen keinen Sinn.

• Die Entropiefunktion  $H'_{\rm bin}(p)$  lautet entsprechend der Angabe:

$$H'_{\rm bin}(p) \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm ln}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm ln}\hspace{0.1cm}\frac{1}{1-p} = {\rm ln}\hspace{0.1cm}2 \cdot \left [ p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p}\right ]$$

$$\Rightarrow \hspace{0.3cm} H'_{\rm bin}(p) \hspace{0.15cm}{\rm (in \hspace{0.15cm} nat)}= {\rm ln}\hspace{0.1cm}2 \cdot H_{\rm bin}(p) \hspace{0.15cm}{\rm (in \hspace{0.15cm} bit)} = 0.693\cdot H_{\rm bin}(p)\hspace{0.05cm}.$$

(2)  Die Optimierungsbedingung lautet  ${\rm d}H_{\rm bin}(p)/{\rm d}p = 0$  bzw.

$$\frac{{\rm d}H'_{\rm bin}(p)}{{\rm d}p} \stackrel{!}{=} 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{\rm d}{{\rm d}p} \big [ - p \cdot {\rm ln}\hspace{0.1cm}p - (1-p) \cdot {\rm ln}\hspace{0.1cm}({1-p})\big ] \stackrel{!}{=} 0$$

$$\Rightarrow \hspace{0.3cm} - {\rm ln}\hspace{0.1cm}p - p \cdot \frac {1}{p}+ {\rm ln}\hspace{0.1cm}(1-p) + (1-p)\cdot \frac {1}{1- p}\stackrel{!}{=} 0$$

$$\Rightarrow \hspace{0.3cm} {\rm ln}\hspace{0.1cm}\frac {1-p}{p}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac {1-p}{p}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline { p = 0.5}\hspace{0.05cm}.$$

• Die Entropiewerte für  $p = 0.5$  lauten somit:

$$H'_{\rm bin}(p = 0.5) \hspace{0.1cm} = \hspace{0.1cm} -2 \cdot 0.5 \cdot {\rm ln}\hspace{0.1cm}0.5 = {\rm ln}\hspace{0.1cm}2 = 0.693 \, {\rm nat}\hspace{0.05cm},$$

$$H_{\rm bin}(p = 0.5) \hspace{0.1cm} = \hspace{0.1cm} -2 \cdot 0.5 \cdot {\rm ld}\hspace{0.1cm}0.5 = {\rm log_2}\hspace{0.1cm}2 \hspace{0.15cm}\underline {= 1 \, {\rm bit}}\hspace{0.05cm}.$$

(3)  Für  $p = 5\%$  erhält man:

$$H_{\rm bin}(p = 0.05) \hspace{0.1cm} = \hspace{0.1cm} 0.05 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.05}+ 0.95 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.95}= \frac{1}{0.693} \cdot \big [ 0.05 \cdot {\rm ln}\hspace{0.1cm}20+ 0.95 \cdot {\rm ln}\hspace{0.1cm}1.053\big ] \hspace{0.15cm}\underline {\approx 0.286 \, {\rm bit}}\hspace{0.05cm}.$$

(4)  Diese Teilaufgabe lässt sich nicht in geschlossener Form lösen, sondern durch „Probieren”.

• Eine Lösung liefert das Ergebnis:

$$H_{\rm bin}(p = 0.10) = 0.469 \, {\rm bit}\hspace{0.05cm},\hspace{0.2cm}H_{\rm bin}(p = 0.12) = 0.529 \, {\rm bit}\hspace{0.05cm},\hspace{0.2cm} H_{\rm bin}(p = 0.11) \approx 0.5 \, {\rm bit} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_1 \approx 0.11\hspace{0.05cm}.$$

• Die zweite (gesuchte) Lösung ergibt sich aus der Symmetrie von  $H_{\rm bin}(p)$  zu  $p_2 = 1 -p_1 \hspace{0.15cm}\underline{= 0.89}$.

(5)  Mit  $p = 0.45$  erhält man  $H_{\rm bin}(p) = 0.993\hspace{0.05cm}\rm bit$.  Der relative Fehler bezüglich Entropie ist somit

$$\varepsilon_{H} = \frac{H_{\rm bin}(p = 0.45)- H_{\rm bin}(p= 0.5)}{H_{\rm bin}(p = 0.5)}= \frac{0.993- 1}{1}\hspace{0.15cm}\underline {= -0.7 \, {\rm \%}} \hspace{0.05cm}.$$

• Das Minuszeichen deutet darauf hin, dass der Entropiewert  $H_{\rm bin}(p) = 0.993\hspace{0.05cm}\rm bit$  zu klein ist.
• Hätte die Simulation den zu großen Wert  $p = 0.55$  ergeben, so wäre die Entropie und auch der relative Fehler genau so groß.

(6)  Es gilt  $H_{\rm bin}(p = 0.045) = 0.265\hspace{0.05cm}\rm bit$.

• Mit dem Ergebnis der Teilaufgabe  (3)   ⇒   $H_{\rm bin}(p = 0.05) = 0.286\hspace{0.05cm}\rm bit$  folgt daraus für den relativen Fehler bezüglich der Entropie:

$$\varepsilon_{H} = \frac{H_{\rm bin}(p = 0.045)- H_{\rm bin}(p= 0.05)}{H_{\rm bin}(p = 0.05)}= \frac{0.265- 0.286}{0.286}\hspace{0.15cm}\underline {= -7.3 \, {\rm \%}} \hspace{0.05cm}.$$

• Das Ergebnis zeigt:

1.  Eine falsche Bestimmung der Symbolwahrscheinlichkeiten um  $10\%$  macht sich für  $p = 0.05$  aufgrund des steileren  $H_{\rm bin}(p)$–Verlaufs deutlich stärker bemerkbar als für  $p = 0.5$.
2.  Eine zu große Wahrscheinlichkeit  $p = 0.055$  hätte zu  $H_{\rm bin}(p = 0.055) = 0.307\hspace{0.05cm}\rm bit$  geführt und damit zu einer Verfälschung um  $\varepsilon_H = +7.3\%$.  In diesem Bereich verläuft die Entropiekurve also (mit guter Näherung) linear.