Aufgabe 1.1: Dual-Slope–Verlustmodell

• Zurück zum Buch

Zum Dual-Slope-Pfadverlustmodell

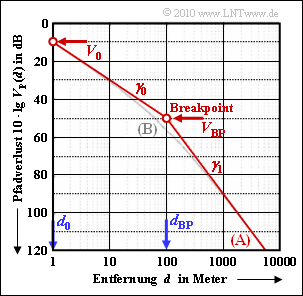
Zur Simulation des Pfadverlustes in städtischer Umgebung verwendet man oft das asymptotische „Dual–Slope–Modell”, das im Diagramm als rote Kurve dargestellt ist.  Dieses Modell ist durch zwei lineare Abschnitte gekennzeichnet, die durch den so genannten Breakpoint  $\rm (BP)$  getrennt sind:

• Für  $d \le d_{\rm BP}$  gilt mit dem Exponenten  $\gamma_0$:

$$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_0})\hspace{0.05cm}.$$

• Für  $d > d_{\rm BP}$  ist der Pfadverlustexponent  $\gamma_1$  anzusetzen, wobei  $\gamma_1 > \gamma_0$  gilt:

$$V_{\rm P}(d) = V_{\rm BP} + \gamma_1 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} ({d}/{d_{\rm BP}})\hspace{0.05cm}.$$

In diesen Gleichungen bedeuten:

• $V_0$  ist der Pfadverlust  (in  „dB”)  bei  $d_0$  (Normierungsdistanz).
• $V_{\rm BP}$  ist der Pfadverlust  (in  „dB”)  bei  $d=d_{\rm BP}$  („Breakpoint”).

Die Grafik gilt für die Modellparameter

$$d_0 = 1\,{\rm m}\hspace{0.05cm},\hspace{0.2cm}d_{\rm BP} = 100\,{\rm m}\hspace{0.05cm},\hspace{0.2cm} V_0 = 10\,{\rm dB}\hspace{0.05cm},\hspace{0.2cm}\gamma_0 = 2 \hspace{0.05cm},\hspace{0.2cm}\gamma_1 = 4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} V_{\rm BP} = 50\,{\rm dB}\hspace{0.05cm}.$$

In den Fragen wird dieser abschnittsweise definierte Verlauf mit Profil  $\rm (A)$ bezeichnet.

Als zweite Kurve ist das Profil  $\rm (B)$  als dünne graue Kurve eingezeichnet, das durch folgende Gleichung gegeben ist:

$$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )\hspace{0.05cm}.$$

Mit diesem Dual–Slope–Modell ist der gesamte Distanzverlauf geschlossen beschreibbar.  Die Empfangsleistung hängt dann von der Distanz  $d$  nach folgender Gleichung ab:

$$P_{\rm E}(d) = \frac{P_{\rm S} \cdot G_{\rm S} \cdot G_{\rm E} /V_{\rm zus}}{K_{\rm P}(d)} \hspace{0.05cm},\hspace{0.2cm}K_{\rm P}(d) = 10^{V_{\rm P}(d)/10} \hspace{0.05cm}.$$

• Hierbei sind alle Parameter absolut einzusetzen, also nicht logarithmisch in „dB”. 
• Die Sendeleistung wird zu  $P_{\rm S} = 5 \ \rm W$  angenommen.

Die weiteren Größen haben folgende Bedeutungen und Werte:

• $10 \cdot \lg \ G_{\rm S} = 17 \ \rm dB$  (Gewinn der Sendeantenne),
• $10 \cdot \lg \ G_{\rm E} = -3 \ \rm dB$  (Gewinn der Empfangsantenne – also eigentlich ein Verlust),
• $10 \cdot \lg \ V_{\rm zus} = 4 \ \rm dB$  (Verlust durch Zuführungen).

Hinweise:

• Die Aufgabe gehört zum Kapitel  Distanzabhängige Dämpfung und Abschattung.
• Würde man das Profil  $\rm (B)$  entsprechend

$$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.15cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right )$$

definieren, so wären Profil  $\rm (A)$  und Profil  $\rm (B)$  für  $d ≥ d_{\rm BP}$  identisch.

• In diesem Fall würde jedoch im unteren Bereich  $(d < d_{\rm BP})$  das Profil  $\rm (B)$  oberhalb von Profil  $\rm (A)$  liegen, und somit deutlich zu gute Verhältnisse suggerieren. Beispielsweise ergäbe sich für  $d = d_0 = 1 \ \rm m$  bei den zugrundeliegenden Zahlenwerten ein um  $40 \ \rm dB$  zu gutes Ergebnis:

$$V_{\rm P}(d) = V_{\rm 0} + \gamma_0 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ( {d}/{d_0} \right ) + (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({d}/{d_{\rm BP}} \right ) =10\,{\rm dB} + 2 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left ({1}/{100} \right ) = -30\,{\rm dB} \hspace{0.05cm}.$$

Fragebogen

1

Wie groß ist der Pfadverlust $($in  $\rm dB)$  nach  $d= 100 \ \rm m$  gemäß Profil  $\rm (A)$?

$V_{\rm P}(d = 100 \ \rm m) \ = \ $ $\ \rm dB$

2

Wie groß ist der Pfadverlust $($in  $\rm dB)$  nach  $d= 100 \ \rm m$  gemäß Profil  $\rm (B)$?

$V_{\rm P}(d = 100 \ \rm m) \ = \ $ $\ \rm dB$

3

Welche Empfangsleistung ergibt sich nach  $100 \ \rm m$  mit beiden Profilen?

Profil $\text{(A):} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ $\ \rm mW$

Profil $\text{(B):} \hspace{0.2cm} P_{\rm E}(d = 100 \ \rm m) \ = \ $ $\ \rm mW$

4

Wie groß ist die Abweichung  $ΔV_{\rm P}$  zwischen Profil  $\rm (A)$  und  $\rm (B)$  bei  $d = 50 \ \rm m$?

$ΔV_{\rm P}(d = 50 \ \rm m) \ = \ $ $\ \rm dB$

5

Wie groß ist die Abweichung  $ΔV_{\rm P}$  zwischen Profil  $\rm (A)$  und  $\rm (B)$  bei  $d = 200 \ \rm m$?

$ΔV_{\rm P}(d = 200 \ \rm m)\ = \ $ $\ \rm dB$

Musterlösung

Musterlösung

(1)  Man erkennt direkt aus der Grafik, dass das Profil  $\rm (A)$  mit den beiden linearen Abschnitten beim „Breakpoint”  $(d = 100 \ \rm m)$  das folgende Ergebnis liefert:

$$V_{\rm P}(d = 100\,{\rm m})\hspace{0.15cm} \underline{= 50\,{\rm dB}} \hspace{0.05cm}.$$

(2)  Mit dem Profil  $\rm (B)$  erhält man dagegen bei Verwendung von  $V_0 = 10 \ \rm dB$,  $\gamma_0 = 2$  und  $\gamma_1 = 4$:

$$V_{\rm P}(d = 100\,{\rm m}) = 10\,{\rm dB} + 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(100)+ 20\,{\rm dB}\cdot {\rm lg} \hspace{0.1cm}(2) \hspace{0.15cm} \underline{\approx 56\,{\rm dB}} \hspace{0.05cm}.$$

(3)  Die Antennengewinne vom Sender  $(+17 \ \rm dB)$  und  Empfänger $(-3 \ \rm dB)$  sowie die internen Verluste der Basisstation  $(+4 \ \rm dB)$  können zusammengefasst werden:

$$10 \cdot {\rm lg}\hspace{0.1cm} G = 10 \cdot {\rm lg}\hspace{0.1cm} G_{\rm S} + 10 \cdot {\rm lg} \hspace{0.1cm} G_{\rm E} - 10 \cdot {\rm lg}\hspace{0.1cm} V_{\rm zus} = 17\,{\rm dB} -3\,{\rm dB} - 4\,{\rm dB} = 10\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {G = 10} \hspace{0.05cm}.$$

• Für das Profil  $\rm (A)$  ergab sich folgender Pfadverlust:

$$V_{\rm P}(d = 100\,{\rm m})\hspace{0.05cm} {= 50\,{\rm dB}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_{\rm P} = 10^5 \hspace{0.05cm}.$$

Damit erhält man für die Empfangsleistung nach  $d = 100 \ \rm m$:

$$P_{\rm E}(d = 100\,{\rm m}) = \frac{P_{\rm S} \cdot G}{K_{\rm P}} = \frac{5\,{\rm W} \cdot 10}{10^5}\hspace{0.15cm} \underline{= 0.5\,{\rm mW}} \hspace{0.05cm}.$$

• Bei Profil  $\rm (B)$  ist die Empfangsleistung etwa um den Faktor  $4$  kleiner:

$$P_{\rm E}(d = 100\,{\rm m}) = \frac{5\,{\rm W} \cdot 10}{10^{5.6}}\approx \frac{5\,{\rm W} \cdot 10}{4 \cdot 10^{5}}\hspace{0.15cm} \underline{= 0.125\,{\rm mW}} \hspace{0.05cm}.$$

(4)  Unterhalb des Breakpoints  $(d < 100 \ \rm m)$  ist die Abweichung durch den letzten Summand von Profil  $\rm (B)$  bestimmt:

$${\rm \Delta}V_{\rm P}(d = 50\,{\rm m}) = (\gamma_1 - \gamma_0) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} \left (1 + {d}/{d_{\rm BP}} \right )= (4-2) \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (1.5)\hspace{0.15cm} \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$

(5)  Hier liefert das Profil  $\rm (A)$  mit $V_{\rm BP} = 50 \ \rm dB$:

$$V_{\rm P}(d = 200\,{\rm m}) = 50\,{\rm dB} + 4 \cdot 10\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (2)\hspace{0.15cm} {\approx 62\,{\rm dB}} \hspace{0.05cm}.$$

• Dagegen führt das Profil  $\rm (B)$  zum Ergebnis:

$$V_{\rm P}(d = 200\,{\rm m}) = 50\,{\rm dB} + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (200) + 20\,{\rm dB} \cdot {\rm lg} \hspace{0.1cm} (3) = 10\,{\rm dB} + 46\,{\rm dB} + 9.5\,{\rm dB} \hspace{0.15cm} {\approx 65.5\,{\rm dB}}$$

$$\Rightarrow \hspace{0.3cm} {\rm \Delta}V_{\rm P}(d = 200\,{\rm m}) = 65.5\,{\rm dB} - 62\,{\rm dB}\hspace{0.15cm} \underline{\approx 3.5\,{\rm dB}} \hspace{0.05cm}.$$

• Man erkennt, dass  $\Delta V_{\rm P}$  nahezu symmetrisch zu  $d = d_{\rm BP}$  ist, wenn man die Entfernung  $d$  wie in der angegebenen Grafik logarithmisch aufträgt.