Aufgabe 2.2Z: Mittlere Codewortlänge

• Zurück zum Buch

Tabelle zur Quellencodierung

Ziel von Datenkomprimierung ist es, die Nachricht einer Quelle mit möglichst wenigen Binärzeichen darzustellen.

Wir betrachten hier eine wertdiskrete Nachrichtenquelle mit dem Symbolvorrat  $\rm \{ A, \ B, \ C, \ D\}$   ⇒   Symbolumfang  $M = 4$  und den Auftrittswahrscheinlichkeiten

• $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$  (Teilaufgabe 1),
• $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$  (ab Teilaufgabe 2).

Vorausgesetzt wird, dass es zwischen den einzelnen Quellensymbolen keine statistischen Bindungen gibt.

Ein Maß für die Güte eines Komprimierungsverfahrens ist die mittlere Codewortlänge  $L_{\rm M}$  mit der Zusatzeinheit „bit/Quellensymbol”.

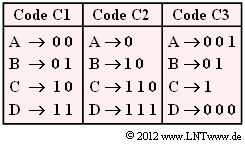
Vorgegeben sind drei Zuordnungen. Anzumerken ist:

• Jeder dieser Binärcodes  $\rm C1$,  $\rm C2$  und  $\rm C3$  ist für eine spezielle Quellenstatistik ausgelegt.
• Alle Codes sind präfixfrei und somit ohne weitere Angabe sofort decodierbar.

Hinweis:

• Die Aufgabe gehört zum Kapitel  Allgemeine Beschreibung der Quellencodierung.

Fragebogen

1

Bestimmen Sie die mittlere Codewortlänge  $L_{\rm M}$  für  $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$.

$\text{C1:}\ \ L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

$\text{C2:}\ \ L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

$\text{C3:}\ \ L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

2

Welche Werte ergeben sich für  $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$?

$\text{C1:}\ \ L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

$\text{C2:}\ \ L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

$\text{C3:}\ \ L_{\rm M} \ = \ $ $\ \rm bit/Quellensymbol$

3

Woran erkennt man präfixfreie Codes?

	Kein Codewort ist der Beginn eines anderen Codewortes.
	Alle Codeworte haben gleiche Länge.

4

Für die spezielle Quellensymbolfolge  $\rm ADBDCBCBADCA$  ergibt sich die Codesymbolfolge  $\rm 001101111001100100111000$.
Welcher Code wurde verwendet?

	Der Code  $\rm C1$,
	der Code  $\rm C2$.

5

Nach Codierung mit  $\rm C3$  erhält man  $\rm 001101111001100100111000$.  Wie lautet die zugehörige Quellensymbolfolge?

	$\rm AACDBACABADAAA$ ...
	$\rm ACBCCCACAACCD$ ...

Musterlösung

Musterlösung

(1)  Die mittlere Codewortlänge ergibt sich allgemein zu

$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}.$$

Sind die vier Quellensymbole gleichwahrscheinlich  $($alle Wahrscheinlichkeiten genau  $1/4)$, so kann dafür auch geschrieben werden:

$$L_{\rm M} = 1/4 \cdot ( L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}) \hspace{0.05cm}.$$

• $\text{Code C1:}$    $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/Quellensymbol$,
• $\text{Code C2:}$    $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$
• $\text{Code C3:}$    $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$.

(2)  Mit der Codetabelle  $\text{C1}$  ergibt sich unabhängig von den Symbolwahrscheinlichkeiten stets die mittlere Codewortlänge  $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \ \rm bit/Quellensymbol$.

Für die beiden anderen Codes erhält man:

• $\text{Code C2:}$    $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/Quellensymbol$,
• $\text{Code C3:}$    $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/Quellensymbol$.

Man erkennt aus dem Beispiel das Prinzip:

• Wahrscheinliche Symbole werden durch wenige Binärsymbole dargestellt, unwahrscheinliche durch mehr.
• Bei gleichwahrscheinlichen Symbolen wählt man am besten auch die Codewortlängen gleich.

(3)  Richtig ist der Lösungsvorschlag 1:

• Der Code  $\text{C1}$  mit einheitlicher Länge aller Codeworte ist präfixfrei,
• aber auch andere Codes können präfixfrei sein, zum Beispiel die Codes  $\text{C2}$  und  $\text{C3}$.

(4)  Richtig ist der Lösungsvorschlag 1:

• Bereits aus „00” am Anfang erkennt man, dass der Code  $\text{C2}$  hier nicht in Frage kommt, da sonst die Quellensymbolfolge mit „AA” beginnen müsste.
• Tatsächlich wurde der Code  $\text{C1}$  verwendet.

(5)  Richtig ist der Lösungsvorschlag 2:

• Der erste Lösungsvorschlag gibt dagegen die Quellensymbolfolge für den Code  $\text{C2}$  an, wenn die Codesymbolfolge  $\rm 001101111001100100111000$  lauten würde.