Aufgabe 4.10: Signalverläufe der 16–QAM

• Zurück zum Buch

Signalverläufe der 16–QAM für
vier beispielhafte Symbole

Wir betrachten das 16–QAM–Verfahren gemäß dem  Blockschaltbild  im Theorieteil.

In aller Kürze lässt sich dieses wie folgt beschreiben:

• Jeweils vier Bit des binären redundanzfreien Quellensignals  $q(t)$  am Eingang ergeben nach Seriell–Parallell–Wandlung und der folgenden Signalraumzuordnung einen komplexwertigen Amplitudenkoeffizienten  

$$a = a_{\rm I} +{\rm j} · a_{\rm Q}.$$

• Mit dem rechteckförmigen Sendegrundimpuls  $g_s(t)$  im Bereich von  $0$  bis  $T$  und der Höhe  $g_0$  erhält man nach den Multiplikationen mit der Cosinus–Funktion bzw. Minus–Sinus–Funktion im betrachteten Zeitintervall:

$$s_{\rm cos}(t) = a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.05cm},$$

$$s_{\rm -sin}(t) = -a_{\rm Q} \cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.05cm}.$$

• Das 16–QAM–Sendesignal ergibt sich dann als Summe dieser beiden Komponentensignale:

$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$

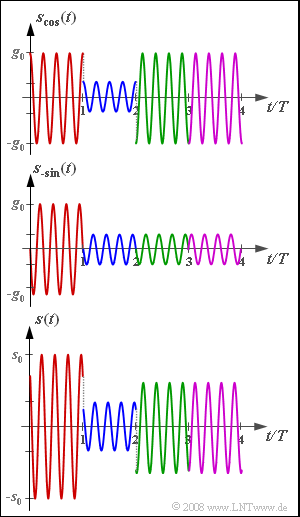
Die Grafik zeigt für vier ausgewählte Symbole die Signale  $s_{\rm cos}(t)$,  $s_{\rm –sin}(t)$  und  $s(t)$. Daraus sollen die Amplitudenkoeffizienten ermittelt werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel  "Quadratur–Amplitudenmodulation".
• Zur Lösung der Aufgabe ist die Seite  "Signalverläufe der 4-QAM"  hilfreich.
• Die betrachtete Signalraumzuordnung ist im Angabenblatt zur  Aufgabe 4.10Z  zu sehen. 
  Auch die farblichen Hervorhebungen passen zusammen.
• Verwenden Sie ab der Teilaufgabe  (6)  die Parameterwerte  $g_0 = 1 \ \rm V$  und  $T = 1 \ \rm µ s$.
• Energien sind in  $\rm V^2s$  anzugeben;  sie beziehen sich somit auf den Bezugswiderstand  $R = 1 \ \rm \Omega$.

Fragebogen

1

Wie lauten Real- und Imaginärteil des Amplitudenkoeffizienten  $a$  im roten Zeitintervall  $(0 < t < T)$?

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

2

Welches Verhältnis besteht zwischen  $s_0$  (maximale Hüllkurve des Sendesignals)  und  $g_0$  (maximale Hüllkurve der Teilsignale)?

$s_0/g_0 \ = \ $

3

Wie lautet der Amplitudenkoeffizient  $a$  im blauen Zeitintervall  $(T < t < 2T)$?

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

4

Wie lautet der Amplitudenkoeffizient  $a$  im grünen Zeitintervall  $(2T < t < 3T)$?  Ermitteln Sie auch dessen Betrag und die Phasenlage.

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

5

Wie lautet der Amplitudenkoeffizient  $a$  im violetten Zeitintervall  $(3T < t < 4T)$?

$a_{\rm I} \ = \ $

$a_{\rm Q} \ = \ $

6

Welche maximale Energie  $E_\text{S, max}$  wird pro Symbol aufgewendet?  Unter welcher Voraussetzung ist die mittlere Energie pro Symbol gleich  $E_\text{S, max}$?

$E_\text{S, max} \ = \ $ $\ \cdot 10^{-6} \ \rm V^2 s$

7

Wie groß ist die maximale Energie  $E_\text{B, max}$  pro Bit?

$E_\text{B, max} \ = \ $ $\ \cdot 10^{-6} \ \rm V^2 s$

8

Wie groß ist die minimale Energie  $E_\text{B, min}$  pro Bit?

$E_\text{B, min} \ = \ $ $\ \cdot 10^{-6} \ \rm V^2 s$

Musterlösung

Musterlösung

(1)  Aus dem (roten) Inphasesignal   ⇒   Realteil folgt  (erste Gleichung entsprechend Definition,  zweite Gleichung gemäß Skizze):

$$s_{\rm cos}(t)= a_{\rm I}\cdot g_0 \cdot \cos(2 \pi f_{\rm T} t)= g_0 \cdot \cos(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm I}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$

• Entsprechend erkennt man aus dem Quadratursignal   ⇒   Imaginärteilteil:

$$s_{\rm -sin}(t)= -a_{\rm Q}\cdot g_0 \cdot \sin(2 \pi f_{\rm T} t)= -g_0 \cdot \sin(2 \pi f_{\rm T} t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}a_{\rm Q}\hspace{0.15cm}\underline {= +1} \hspace{0.05cm}.$$

(2)  Die beiden Teilsignale haben jeweils die  (maximale)  Hüllkurve  $g_0$,  während  $s_0$  das Sendesignal  $s(t)$  charakterisiert.

• Wie aus der Signalraumzuordnung  (siehe Aufgabe 4.10Z)  hervorgeht, gilt:

$${s_0}/{ g_0 }= \sqrt{2}\hspace{0.15cm}\underline { = 1.414} \hspace{0.05cm}.$$

(3)  Die Amplitudenkoeffizienten  $a_{\rm I}$  und  $a_{\rm Q}$  haben die gleichen Vorzeichen wie bei der Teilaufgabe  (1),  aber mit kleinerem Betrag:

$$a_{\rm I} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$

(4)  Im dritten  (grünen)  Intervall erkennt man ein Minus–Cosinus–Signal mit der Amplitude  $g_0$  und ein Minus–Sinus–Signal mit Amplitude  $g_0/3$:

$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = + 1/3\hspace{0.15cm}\underline {= +0.333} \hspace{0.05cm}.$$

• Wie in der Teilaufgabe  (4)  der Aufgabe 4.10Z noch berechnet werden soll,  ist hier der Betrag gleich  $|a| =1.054$  und der Phasenwinkel  ${\rm arc} \ a \approx 161^\circ$.

(5)  Das violette Signal unterscheidet sich vom grünen Intervall nicht in der Inphasekomponente,  sondern nur im Vorzeichen der Quadraturkomponente:

$$a_{\rm I} = \hspace{0.15cm}\underline {= -1} \hspace{0.05cm},\hspace{0.5cm}a_{\rm Q} = - 1/3\hspace{0.15cm}\underline {= -0.333} \hspace{0.05cm}.$$

(6)  Die maximale Signalenergie tritt auf,  wenn einer der vier äußeren Eckpunkte belegt ist.  Dann gilt:

$$E_{\rm S, \hspace{0.05cm}max} = {1}/{2}\cdot s_0^2 \cdot T = {1}/{2}\cdot \left (\sqrt{2} \cdot g_0 \right )^2 \cdot T = g_0^2 \cdot T = (1\,{\rm V})^2 \cdot (1\,{\rm \mu s}) \hspace{0.15cm}\underline {= 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$

• Die mittlere Signalenergie ist gleich dem Maximalwert,  wenn nur die Eckpunkte der Signalraumzuordnung belegt sind und „innere Symbole” von der Codierung ausgeschlossen werden.

(7)  Pro Symbol werden vier Bit übertragen.  Daraus folgt:

$$E_{\rm B, \hspace{0.05cm}max} = {E_{\rm S, \hspace{0.05cm}max}}/{4}\hspace{0.15cm}\underline {= 0.25 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$

(8)  Die minimale Signalenergie ergibt sich bei einem der inneren Signalraumpunkte und ist um den Faktor  $9$  kleiner als bei Teilaufgabe  (7):

$$E_{\rm B, \hspace{0.05cm}min} = \frac{E_{\rm B, \hspace{0.05cm}max}}{9} = \frac{g_0^2 \cdot T}{36} \hspace{0.15cm}\underline { \approx 0.028 \cdot 10^{-6}\,{\rm V^2s}}\hspace{0.05cm}.$$

• Im Theorieteil wird gezeigt,  dass bei der 16–QAM für die mittlere Signalenergie pro Bit unter der Voraussetzung,  dass alle Symbole gleichwahrscheinlich sind,  näherungsweise gilt:

$$E_{\rm B} \approx 0.139 · g_0^2 \cdot T = 0.035 \cdot 10^{-6}\,{\rm V^2s}.$$