Aufgabe 1.12Z: Vergleich von HC (7, 4, 3) und HC (8, 4, 4)
Nun sollen die Blockfehlerwahrscheinlichkeiten
- des $(7, 4, 3)$–Hamming–Codes und
- des erweiterten $(8, 4, 4)$–Hamming–Codes
miteinander verglichen werden. Zugrunde gelegt werden
- das "BSC–Kanalmodell" (Parameter $\varepsilon$, insbesondere $\varepsilon = 0.01$ für numerische Ergebnisse),
- die "Syndromdecodierung", mit der bei beiden Codes eine Maximum–Likelihood–Detektion realisiert wird; bei richtiger Belegung der Syndromtabelle ergibt sich jeweils die minimale Blockfehlerwahrscheinlichkeit.
Für den $(7, 4, 3)$–Code wurde in der "Aufgabe 1.12" exakt berechnet:
- $${\rm Pr(Blockfehler)} = 1 - (1 - \varepsilon)^7 - 7 \cdot \varepsilon \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$
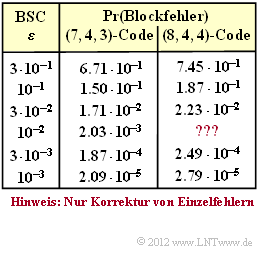
Die Zahlenwerte sind in der zweiten Spalte der obigen Tabelle angegeben. Es handelt sich um die tatsächlichen Werte, also nicht um die in "Aufgabe 1.12" hergeleitete Näherung ${\rm Pr(Blockfehler)} \approx 21 \cdot \varepsilon^2$.
Anzumerken ist, dass aufgrund des BSC–Kanalmodells nur harte Entscheidungen möglich sind. Mit "Soft Decision" ergeben sich etwas kleinere Blockfehlerwahrscheinlichkeiten.
Nun soll die Blockfehlerwahrscheinlichkeit für den erweiterten $(8, 4, 4)$–Code ermittelt werden:
- Die Berechnung in Teilaufgabe (4) erfolgt unter der Maßgabe, dass wie beim $(7, 4, 3)$–Code nur solche Fehlermuster mit einer einzigen „$1$” korrigiert werden. In der rechten Spalte obiger Tabelle sind die Ergebnisse eingetragen, bis auf den Wert für $\varepsilon = 0.01$, der explizit berechnet werden soll.
- In der Teilaufgabe (5) soll dagegen berücksichtigt werden, dass beim erweitereten $(8, 4, 4)$–Code Teile der Syndromtabelle noch mit Gewicht–2–Fehlermustern aufgefüllt werden können.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Decodierung linearer Blockcodes".
- Von Interesse für die Lösung dieser Aufgabe ist insbesondere die Seite "Verallgemeinerung der Syndromdecodierung".
Fragebogen
Musterlösung
- Beim $(7, 4, 3)$–Hamming–Code ist $m = n - k = 3$ ⇒ die Länge der Tabelle ist $N_{\rm ges} =2^3 \ \underline{= 8}.$
- Die Syndromtabelle des $(8, 4, 4)$–Codes ist doppelt so groß: $N_{\rm ges} = 2^4 \ \underline{= 16}$.
(2) Allgemein gilt für die Anzahl der Einträge mit Gewicht–2–Fehlermustern: $N_2' = $ "$n {\rm \ über \ } 2$". Daraus ergeben sich die Zahlenwerte
- $N_2' \ \underline{= 21} \ $ für $n = 7 \ \ ⇒ \ \ (7, 4, 3)$–Code,
- $N_2' \ \underline{= 28} \ $ für $n = 8 \ \ \Rightarrow \ \ (8, 4, 4)$–Code.
(3) Beim $(7, 4, 3)$–Hamming–Code ist die Syndromtabelle gefüllt
- mit einem Eintrag für den fehlerfreien Fall $(N_{0}= 1)$
- und $n = 7$ Einträge mit Gewicht–1–Fehlermustern $(N_{1} = 7)$.
Damit ist die Anzahl der Einträge mit Gewicht–2–Fehlermustern gleich
- $$N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 0} \hspace{0.05cm}.$$
Dagegen gilt für den erweiterten $(8, 4, 4)$–Hamming–Code:
- $$N_0 = 1\hspace{0.05cm},\hspace{0.2cm}N_1 = 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} N_2 = N_{\rm ges} - N_0 - N_1 \hspace{0.15cm} \underline{= 7} \hspace{0.05cm}.$$
(4) Analog zur Musterlösung der ersten beiden Teile von Aufgabe 1.12 erhält man hier:
- $${\rm Pr(Blockfehler)} = 1 - (1 - \varepsilon)^8 - 8 \cdot \varepsilon \cdot (1 - \varepsilon)^7$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr(Blockfehler)} =1 - 0.922745 - 0.074655\hspace{0.15cm} \underline{= 2.69 \cdot 10^{-3}} \hspace{0.05cm}.$$
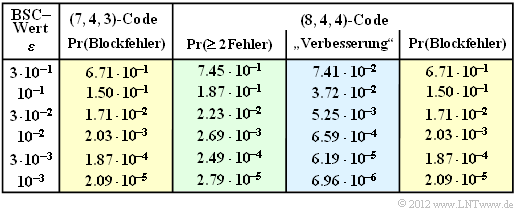
- In der Tabelle sind für diesen Fall und für verschiedene BSC–Parameter $ε$ die Ergebnisse in der dritten Spalte ⇒ ${\rm Pr}(\ge \text{2 Fehler)}$ eingetragen.
- Gegenüber dem $(7, 4, 3)$–Code entsprechend der zweiten Spalte ergibt sich stets eine Verschlechterung.
(5) Bei bestmöglicher Korrektur (gefüllte Syndromtabelle) werden auch sieben Gewicht–2–Fehlermuster korrigiert.
- Damit vermindert sich die Blockfehlerwahrscheinlichkeit um die „Verbesserung” (Spalte 4):
- $${\rm Pr(Gewicht\hspace{-0.1cm}-\hspace{-0.1cm}2\hspace{-0.1cm}-\hspace{-0.1cm}Fehlermuster\hspace{0.15cm} wird \hspace{0.15cm} korrigiert)} = 7 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$
- Für $\varepsilon = 0.01$ macht diese „Verbesserung” etwa $6.59 · 10^{–4}$ aus.
- Die Blockfehlerwahrscheinlichkeit des $(8, 4, 4)$–Codes (letzte Spalte) ergibt sich somit zu
- $${\rm Pr(Blockfehler)} = 2.69 \cdot 10^{-3} - 0.66 \cdot 10^{-3} \underline{= 2.03 \cdot 10^{-3}} \hspace{0.05cm}.$$
In der obigen Tabelle ist diese Rechnung für verschiedene BSC–Parameter $\varepsilon$ durchgeführt. Man erkennt:
- Die Blockfehlerwahrscheinlichkeit des erweiterten $(8, 4, 4)$–Hamming–Codes (letzte Spalte) stimmt exakt mit der des $(7, 4, 3)$–Hamming–Codes (Spalte 2) überein.
- Die Korrektur von $25\%$ der Gewicht–2–Fehlermuster gleicht genau die Tatsache aus, dass beim $(8, 4, 4)$–Code Fehlermuster mit mehr als einem Fehler (Spalte 3) wahrscheinlicher sind als beim $(7, 4, 3)$–Code (Spalte 2).