Aufgabe 1.3: Entropienäherungen

• Zurück zum Buch

Verschiedene Binärfolgen

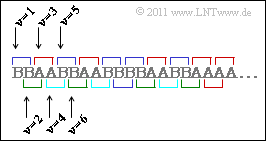
Die Grafik rechts oben zeigt vier Symbolfolgen  $\langle q_\nu \rangle$  mit jeweiliger Länge  $N = 60$.  Die Quellensymbole sind jeweils  $\rm A$  und  $\rm B$.

• Daraus folgt direkt, dass für den Entscheidungsgehalt aller betrachteten Quellen  $H_0 = 1 \; \rm bit/Symbol$  gilt.
• Die Symbole  $\rm A$  und  $\rm B$  treten jedoch nicht gleichwahrscheinlich auf, sondern mit den Wahrscheinlichkeiten  $p_{\rm A}$  und  $p_{\rm B}$.

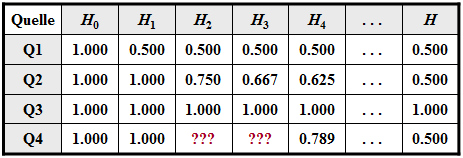
Die untere Tabelle zeigt neben  $H_0$  noch die Entropienäherungen

• $H_1$,  basierend auf  $p_{\rm A}$  und  $p_{\rm B}$  (Spalte 2),
• $H_2$,  basierend auf Zweiertupel (Spalte 3),
• $H_3$,  basierend auf Dreiertupel (Spalte 4),
• $H_4$,  basierend auf Vierertupel (Spalte 5),
• die tatsächliche Entropie  $H$, die sich aus  $H_k$  durch den Grenzübergang für  $k \to \infty$  ergibt (letzte Spalte).

Zwischen diesen Entropien bestehen folgende Größenrelationen:   $H \le$ ... $\le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$

• Nicht bekannt ist die Zuordnung zwischen den Quellen  $\rm Q1$,  $\rm Q2$,  $\rm Q3$,  $\rm Q4$  und den in der Grafik gezeigten gezeigten Symbolfolgen  (Schwarz, Blau, Rot, Grün).
• Es ist lediglich bekannt, dass die Quelle  $\rm Q4$  einen Wiederholungscode beinhaltet.  Aufgrund der Tatsache, dass bei der entsprechenden Symbolfolge jedes zweite Symbol keinerlei Information lierfert, ist die Entropie  $H = 0.5 \; \rm bit/Symbol$.
• Zudem sind die Näherungen  $H_1 = 1 \; \rm bit/Symbol$  und  $H_4 \approx 0.789 \; \rm bit/Symbol$  gegeben.

Zu bestimmen sind für diese Nachrichtenquelle  $\rm Q4$  schließlich noch die Entropienäherungen  $H_2$  und  $H_3$.

Quellenentropie und Näherungen in „bit/Symbol”

Hinweise:

• Die Aufgabe gehört zum Kapitel  Nachrichtenquellen mit Gedächtnis.

• Für die  $k$–te Entropienäherung gilt bei Binärquellen  $(M = 2)$  mit der Verbundwahrscheinlichkeit  $p_i^{(k)}$  eines  $k$–Tupels:

$$H_k = \frac{1}{k} \cdot \sum_{i=1}^{2^k} p_i^{(k)} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p_i^{(k)}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol}) \hspace{0.05cm}.$$

Fragebogen

1

Von welcher Quelle stammt die schwarze Symbolfolge?

	$\rm Q1$,
	$\rm Q2$,
	$\rm Q3$,
	$\rm Q4$.

2

Von welcher Quelle stammt die blaue Symbolfolge?

	$\rm Q1$,
	$\rm Q2$,
	$\rm Q3$,
	$\rm Q4$.

3

Von welcher Quelle stammt die rote Symbolfolge?

	$\rm Q1$,
	$\rm Q2$,
	$\rm Q3$,
	$\rm Q4$.

4

Berechnen Sie die Entropienäherung  $H_2$  des Wiederholungscodes  $\rm Q4$.

$H_2 \ = \ $ $\ \rm bit/Symbol$

5

Berechnen Sie die Entropienäherung  $H_3$  des Wiederholungscodes  $\rm Q4$.

$H_3 \ = \ $ $\ \rm bit/Symbol$

Musterlösung

Musterlösung

(1)  Die schwarze Binärfolge stammt von der Quelle  $\underline{\rm Q3}$,

• da die Symbole gleichwahrscheinlich sind   ⇒   $H_1 = H_0$,  und
• keine statistischen Bindungen zwischen den Symbolen bestehen   ⇒   $H=$ ... $= H_2 = H_1$.

(2)  Man erkennt bei der blauen Binärfolge, dass  $\rm A$  sehr viel häufiger auftritt als  $\rm B$, so dass  $H_1 < H_0$  gelten muss.

• Entsprechend der Tabelle erfüllt nur die Quelle  $\underline{\rm Q1}$  diese Bedingung.
• Aus  $H_1 = 0.5 \; \rm bit/Symbol$  kann man die Symbolwahrscheinlichkeiten  $p_{\rm A} = 0.89$  und  $p_{\rm B} = 0.11$  ermitteln.

(3)  Durch Ausschlussverfahren kommt man für die rote Binärfolge zum Ergebnis  $\underline{\rm Q2}$:

• Die Quelle  $\rm Q1$  gehört nämlich zur blauen Folge,  $\rm Q3$  zur schwarzen und  $\rm Q4$  zum Wiederholungscode und damit offensichtlich zur grünen Symbolfolge.
• Die rote Symbolfolge weist folgende Eigenschaften auf:

• Wegen  $H_1 = H_0$  sind die Symbole gleichwahrscheinlich:   $p_{\rm A} = p_{\rm B} = 0.5$.
• Wegen  $H < H_1$  bestehen statistische Bindungen innerhalb der Folge.

• Diese erkennt man daran, dass es zwischen  $\rm A$  und  $\rm B$  mehr Übergänge als bei statistischer Unabhängigkeit gibt.

(4)  Bei der grünen Symbolfolge  $($Quelle $\rm Q4)$  sind die Symbole  $\rm A$  und  $\rm B$  gleichwahrscheinlich:

Symbolfolgen eines binären Wiederholungscodes

$$p_{\rm A} = p_{\rm B} = 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_1 = 1\,{\rm bit/Symbol} \hspace{0.05cm}.$$

Zur  $H_2$–Ermittlung betrachtet man Zweiertupel.  Die Verbundwahrscheinlichkeiten  $p_{\rm AA}$,  $p_{\rm AB}$,  $p_{\rm BA}$  und  $p_{\rm BB}$  können daraus berechnet werden.  Aus der Skizze erkennt man:

• Die Kombinationen  $\rm AB$  und  $\rm BA$  sind nur dann möglich, wenn ein Tupel bei geradzahligem  $\nu$  beginnt.  Für die Verbundwahrscheinlichkeiten  $p_{\rm AB}$  und  $p_{\rm BA}$  gilt dann:

$$p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} {\rm Pr}(\nu {\rm \hspace{0.15cm}ist\hspace{0.15cm}gerade}) \cdot {\rm Pr}( q_{\nu} = \mathbf{A}) \cdot {\rm Pr}(q_{\nu+1} = \mathbf{B}\hspace{0.05cm} | q_{\nu} = \mathbf{A}) = {1}/{2} \cdot {1}/{2} \cdot {1}/{2} = {1}/{8} = p_{\rm BA} \hspace{0.05cm}.$$

• Dagegen gelten für die beiden weiteren Kombinationen  $\rm AA$  und  $\rm BB$:

$$p_{\rm AA} ={\rm Pr}(\nu = 1) \cdot {\rm Pr}( q_1 = \mathbf{A}) \cdot {\rm Pr}(q_{2} = \mathbf{A}\hspace{0.05cm} | q_{1} = \mathbf{A}) + {\rm Pr}(\nu=2) \cdot {\rm Pr}( q_{2} = \mathbf{A}) \cdot {\rm Pr}(q_{3} = \mathbf{A}\hspace{0.05cm} | q_{2} = \mathbf{A}) \hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.3cm}p_{\rm AA} = \frac{1}{2} \cdot \frac{1}{2} \cdot 1+ \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{8} = p_{\rm BB} \hspace{0.05cm}.$$

Hierbei steht  $\nu = 1$  für alle ungeradzahligen Indizes und  $\nu = 2$  für alle geradzahligen Indizes.

• Damit ergibt sich für die Entropienäherung:

$$H_2 = \frac{1}{2} \cdot \left [ 2 \cdot \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}\frac {8}{3} + 2 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] = \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) - \frac{3}{8} \cdot {\rm log}_2\hspace{0.1cm}(3) + \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

(5)  Nach ähnlichem Vorgehen kommt man bei Dreiertupeln zu den Verbundwahrscheinlichkeiten

$$p_{\rm AAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBB} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm ABA} = p_{\rm BAB} = 0 \hspace{0.05cm},\hspace{0.2cm} p_{\rm AAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABB} = p_{\rm BBA} = p_{\rm BAA} = 1/8$$

und daraus zur Entropienäherung

$$H_3 = \frac{1}{3} \cdot \left [ 2 \cdot \frac{1}{4} \cdot {\rm log}_2\hspace{0.1cm}(4) + 4 \cdot \frac{1}{8} \cdot {\rm log}_2\hspace{0.1cm}(8)\right ] = \frac{2.5}{3} \hspace{0.15cm} \underline {= 0.833 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

Zur Berechnung von  $H_4$  ergeben sich folgende  $16$  Wahrscheinlichkeiten:

$$p_{\rm AAAA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm BBBB} = 3/16 \hspace{0.05cm},\hspace{0.2cm} p_{\rm AABB} = p_{\rm BBAA} = 2/16 \hspace{0.05cm},$$

$$p_{\rm AAAB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABBA} = p_{\rm ABBB} = p_{\rm BBBA} = p_{\rm BAAB} = p_{\rm BAAA}= 1/16 \hspace{0.05cm}$$

$$p_{\rm AABA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm ABAA} = p_{\rm ABAB} = p_{\rm BBAB} = p_{\rm BABB} = p_{\rm BABA}= 0\hspace{0.05cm}.$$

Daraus folgt:

$$H_4= \frac{1}{4} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\left [ 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{3}{16} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.1cm}\frac{16}{3} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{1}{8} \hspace{-0.05cm}\cdot \hspace{-0.05cm}{\rm log}_2\hspace{0.1cm}(8) + 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{1}{16} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.1cm}(16)\right ] =\frac{\left [ 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(16) - 6 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(3) + 4 \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(8) + 6\hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.01cm}(16)\right ]}{32} .$$

Man erkennt:

• Auch die Näherung  $H_4 = 0.789\,{\rm bit/Symbol}$  weicht noch deutlich vom Entropie-Endwert  $H = 0.5\,{\rm bit/Symbol}$  ab.
• Der Wiederholungscode kann offensichtlich nicht durch eine Markovquelle modelliert werden.  Wäre  $\rm Q4$  eine Markovquelle, so müsste nämlich gelten:

$$H = 2 \cdot H_2 - H_1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}H_2 = 1/2 \cdot (H+H_1) = 1/2 \cdot (0.5+1) = 0.75 \,{\rm bit/Symbol}\hspace{0.05cm}.$$