Aufgabe 1.5: Idealer rechteckförmiger Tiefpass

• Zurück zum Buch

Tabelle mit Werten der  $\rm si$–Funktion und der  $\rm Si$–Funktion

Wir betrachten einen idealen, rechteckförmigen Tiefpass – auch Küpfmüller–Tiefpass genannt,

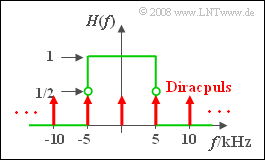
• der alle Frequenzen  $f < 5 \ \rm kHz$  unverfälscht durchlässt   ⇒   $H(f) = 1$,
• und alle Spektralanteile über  $5 \ \rm kHz$  vollständig unterdrückt   ⇒   $H(f) = 0$.

Exakt bei der Grenzfrequenz  $f_{\rm G} = 5 \ \rm kHz$  ist der Wert der Übertragungsfunktion gleich  $1/2$.

An den Eingang des Tiefpasses werden verschiedene Signale angelegt:

• ein schmaler Rechteckimpuls geeigneter Höhe, der durch einen „Dirac” angenähert werden kann:

$$x_1(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot {\rm \delta}(t),$$

• ein Diracpuls, also eine Summe von Diracimpulsen im jeweiligen Zeitabstand  $T_{\rm A}$:

$$x_2(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot \sum_{\nu = -\infty}^{+\infty}{\rm \delta}(t - \nu \cdot T_{\rm A}),$$

wobei das zugehörige Spektrum mit  $f_{\rm A} = 1/T_{\rm A}$  lautet:

$$X_2(f) = \frac{10^{-3}\hspace{0.1cm}{\rm Vs}}{T_{\rm A}} \cdot\sum_{\mu = -\infty}^{+\infty}{\rm \delta}(f - \mu \cdot f_{\rm A}),$$

• eine Sprungfunktion zum Zeitpunkt  $t = 0$:

$$x_3(t) = 10\hspace{0.1cm}{\rm V} \cdot \gamma(t) = \left\{ \begin{array}{c} 0 \\ 5\hspace{0.1cm}{\rm V} \\ 10\hspace{0.1cm}{\rm V} \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{ t < 0,} \\{ t = 0,} \\ { t > 0,} \\ \end{array}$$

• ein  $\rm si$–förmiger Impuls mit der äquivalenten Dauer  $T$:

$$x_4(t) = 10\hspace{0.1cm}{\rm V} \cdot {\rm si}(\pi \cdot {t}/{T}) \hspace{0.5cm} {\rm mit} \hspace{0.5cm} {\rm si}(x) = {\rm sin}(x)/x .$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Einige systemtheoretische Tiefpassfunktionen.
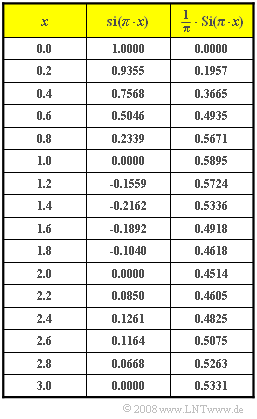
• In der Tabelle sind die Funktionswerte der Spaltfunktion  ${\rm si}(πx)$ und der Integralsinusfunktion  ${\rm Si}(πx)$ aufgelistet:

$${\rm Si}(\pi x) = \int_{ 0 }^{ x } {{\rm si} ( \pi \xi )} \hspace{0.1cm}{\rm d}\xi \hspace{0.5cm}{\rm mit } \hspace{0.5cm} {\rm si}(x) =\sin(x)/x.$$

Fragebogen

1

Welches Ausgangssignal  $y_1(t)$  ergibt sich als Antwort auf den Diracimpuls  $x_1(t)$, insbesondere zu den Zeitpunkten  $t = 0$  und  $t = 50 \ \rm µ s$?

$y_1(t = 0) \ = \ $  $\rm V$

$y_1(t = 50 {\: \rm µ s}) \ = \ $  $\rm V$

2

Wie lautet das Ausgangssignal  $y_2(t)$, wenn am Filtereingang der Diracpuls  $x_2(t)$  anliegt und  $T_{\rm A} = 200 \ µ \rm s$  gilt. Welcher Signalwert tritt bei  $t = 0$  auf?

$y_2(t = 0) \ = \ $  $\rm V$

3

Welche Werte  $y_2(t = 0)$  ergeben sich mit  $T_{\rm A} = 199 \ \rm µ s$  bzw.  $T_{\rm A} = 201 \ \rm µ s$?

$T_{\rm A} = 199 \ {\rm µ s} \text{:}\hspace{0.4cm} y_2(t = 0) \ = \ $  $\rm V$

$T_{\rm A} = 201 \ {\rm µ s} \text{:}\hspace{0.4cm} y_2(t = 0) \ = \ $  $\rm V$

4

Geben Sie das Ausgangssignal  $y_3(t)$  für die Sprungfunktion  $x_3(t)$  mit Endwert  $10 \ \rm V$  an. Welcher Signalwert tritt zum Zeitpunkt  $t = 0$  auf?

$y_3(t = 0) \ = \ $  $\rm V$

5

Zu welcher Zeit  $t_{\rm max}$  ist  $y_3(t)$  maximal? Wie groß ist der Maximalwert?

$t_{\rm max} \ = \ $  $\rm µ s$

$y_3(t_{\rm max}) \ = \ $  $\rm V$

6

Wie lautet das Ausgangssignal  $y_4(t)$, wenn am Eingang das  ${\rm si}$–förmige Signal  $x_4(t)$  mit  ${\rm si}(πx)$ $T = 200 \ \rm µ s$  anliegt? Welcher Wert ergibt sich für  $t = 0$?

$y_4(t = 0) \ = \ $  $\rm V$

7

Welcher Signalwert  $y_4(t = 0)$  ergibt sich für  $T = 50 \ \rm µ s$?

$y_4(t = 0) \ = \ $  $\rm V$

Musterlösung

Musterlösung

(1)  Die Impulsantwort des idealen Tiefpasses lautet mit  $Δf = 10 \ \rm kHz$:

$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t ).$$

• Das Ausgangssignal unterscheidet sich hiervon um den Gewichtungsfaktor  $\rm 10^{–3} \ \rm Vs$:

$$y_1(t) = 10^{-3}\hspace{0.1cm}{\rm Vs} \cdot 10^{4}\hspace{0.1cm}{\rm Hz} \cdot {\rm si}(\pi \cdot \Delta f \cdot t ) = 10\hspace{0.1cm}{\rm V} \cdot {\rm si}(\pi \cdot \Delta f \cdot t )$$

$$\Rightarrow \hspace{0.2cm}y_1(t = 0) \hspace{0.15cm}\underline{=10\hspace{0.1cm}{\rm V}},\hspace{0.5cm}y_1(t = 50\hspace{0.1cm}{\rm µ s}) =10\hspace{0.1cm}{\rm V} \cdot {\rm si} \left( {\pi}/{2} \right) \hspace{0.15cm}\underline{= 6.37\hspace{0.1cm}{\rm V}}.$$

Diracpuls und Rechteckfilter

(2)  Das Spektrum  $X_2(f)$  beinhaltet diskrete Linien im Abstand  $f_{\rm A} = 1/T_{\rm A} = 5 \ \rm kHz$, jeweils mit Gewicht  $5 \ \rm V$.

• Das Spektrum  $Y_2(f)$  besteht somit aus einer Spektrallinie bei  $f = 0$  mit dem Gewicht  $5 \ \rm V$  und je einer bei  $±5 \ \rm kHz$  mit dem Gewicht  $2.5 \ \rm V$. Damit gilt für das Zeitsignal:

$$y_2(t) = 5 \hspace{0.1cm}{\rm V} + 5\hspace{0.1cm}{\rm V} \cdot{\rm cos}(2 \pi \cdot f_{\rm A} \cdot t ) = 10\hspace{0.1cm}{\rm V} \cdot {\rm cos}^2(\pi \cdot f_{\rm A} \cdot t ).$$

$$\Rightarrow \hspace{0.3cm} y_2(t= 0) \hspace{0.15cm} \underline{ = 10\hspace{0.1cm}{\rm V}} .$$

(3)  Mit  $T_{\rm A} = 199 \ \rm µ s$  ist  $f_{\rm A} > 5 \ \rm kHz$. Wegen  $H(f_{\rm A}) = 0$  besteht somit das Spektrum aus nur einer Spektrallinie bei  $f = 0$  mit dem Gewicht  $5.025 \ \rm V$  und man erhält den konstanten Verlauf

$$\Rightarrow \hspace{0.3cm} y_2(t) \rm \underline{\: = 5.025 \ \rm V}.$$

• Wird  $T_{\rm A}$  weiter verringert, so ergibt sich am Ausgang weiterhin ein Gleichsignal, aber mit größerem Signalwert  $($proportional zu  $1/T_{\rm A})$.

• Dagegen ist mit  $T_{\rm A} = 201 \ \rm µ s$  die Abtastfrequenz etwas kleiner als die Grenzfrequenz des Filters  $(5 \ \rm kHz)$, und die Spektralfunktion des Ausgangssignals lautet:

$$Y_2(f) = 4.975\hspace{0.1cm}{\rm V} \cdot \big[ {\rm \delta}(f ) + {\rm \delta}(f + f_{\rm A}) + {\rm \delta}(f - f_{\rm A})\big].$$

• Daraus folgt für das Zeitsignal:

$$y_2(t ) = 4.975\hspace{0.1cm}{\rm V} + 9.95\hspace{0.1cm}{\rm V} \cdot {\rm cos}(2 \pi \cdot f_{\rm A} \cdot t ) \hspace{0.2cm} \Rightarrow \hspace{0.2cm}y_2(t = 0) \hspace{0.15cm}\underline{=14.925\hspace{0.1cm}{\rm V}}.$$

• Am prinzipiellen Verlauf ändert sich nichts, so lange  $200 \ {\rm µ s} < T_{\rm A} < 400 \ {\rm µ s}$  gilt.
• Allerdings ergeben sich je nach  $T_{\rm A}$  unterschiedliche Amplituden.   Für  $T_{\rm A} ≥ 400 \ {\rm µ s}$ kommen weitere Spektrallinien hinzu.

Impulsantwort und Sprungantwort

(4)  Das Ausgangssignal  $y_3(t)$  verläuft nun entsprechend der Integralsinusfunktion:

$$y_3(t = 0) = 10\hspace{0.1cm}{\rm V} \cdot \Delta f \cdot \int_{ - \infty }^{ t } \hspace{-0.3cm} {{\rm si} ( \pi \Delta f \tau )} \hspace{0.1cm}{\rm d}\tau = 10\hspace{0.1cm}{\rm V} \cdot \big[ {1}/{2} + {1}/{\pi}\cdot {\rm Si} ( \pi \Delta f t )\big].$$

$$\Rightarrow \hspace{0.3cm} y_3(t= 0) \hspace{0.15cm} \underline{ = 5\hspace{0.1cm}{\rm V}} .$$

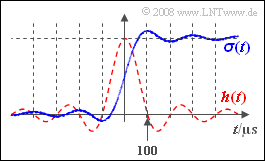
(5)  Es ist offensichtlich, dass  $y_3(t)$  dann maximal ist, wenn die  ${\rm si}$–Funktion zum ersten Mal bei positiven Zeiten die Abszisse schneidet (siehe Skizze). Also muss gelten:

$$t_{\rm max} = 1/Δf \rm \underline{\: = 100 \: µ s}.$$

• Der Signalwert ergibt sich entsprechend der Tabelle auf der Angabenseite zu

$$y_3(t = t_{\rm max}) = 10\hspace{0.1cm}{\rm V} \cdot \big[ {1}/{2} + {1}/{\pi}\cdot {\rm Si} ( \pi )\big]= 10\hspace{0.1cm}{\rm V} \cdot \big[ 0.5 + 0.5895 \big] \hspace{0.15cm}\underline{= 10.895 \hspace{0.1cm}{\rm V}} .$$

• Zu späteren Zeiten  $t$  schwingt  $y_3(t)$  langsam auf seinen Endwert  $10 \ \rm V$ ein.

Rechteckspektren am Eingang des Rechteckfilters

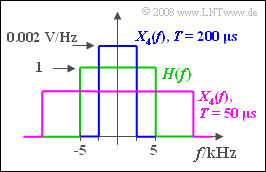
(6)  Die Spektralfunktion  $X_4(f)$  ist wie  $H(f)$  rechteckförmig und für  $|f| > 2.5 \ \rm kHz$  stets Null.

• Das bedeutet, dass  $Y_4(f ) = X_4(f)$  gilt und somit auch  $y_4(t) = x_4(t)$.
• Damit ist  $y_4(t = 0) \rm \underline{\: = 10 \: \rm V}$.

(7)  Mit  $T = 50 \ \rm µ s$  hat  $X_4(f)$  die Breite  $20 \ \rm kHz$  und die Höhe  $0.5 · 10 ^{-3} \ \rm V/Hz$.

• Die Spektralfunktion  $Y_4(f)$  nach Multiplikation mit  $H(f)$  hat die gleiche Höhe.
• Die Breite  $10 \ \rm kHz$  wird nun ausschließlich durch  $H(f)$  bestimmt:

$$y_4(t) = 0.5 \cdot 10^{-3}\hspace{0.1cm}{ {\rm V} }/{ {\rm Hz} } \cdot 10 \hspace{0.1cm}{\rm kHz} \cdot {\rm si}(\pi \Delta f t ) = 5\hspace{0.1cm}{\rm V} \cdot {\rm si}(\pi \Delta f t )$$

$$\Rightarrow \hspace{0.3cm}y_4(t = 0) \hspace{0.15cm}\underline{=5\hspace{0.1cm}{\rm V} }.$$