Aufgabe 2.1: Gruppe, Ring, Körper

• Zurück zum Buch

„Addition” und „Multiplikation”
  für  $q = 3$  und  $q = 4$

Im  "Theorieteil"  zu diesem Kapitel wurden verschiedene algebraische Begriffe definiert. Für das Folgende setzen wir voraus,  dass alle Mengen aus jeweils  $q$  Elementen bestehen,  wobei hier entweder  $q = 3$  oder  $q = 4$  gelten soll.  Dann gilt:

• Eine  "algebraische Gruppe"  ist eine endliche Menge  $G = \{0, \, 1, \hspace{0.05cm}\text{...} \hspace{0.1cm} , \ q-1\}$  zusammen mit einer zwischen allen Elementen definierten Verknüpfungsvorschrift.  $(G, \ +)$  bezeichnet eine additive Gruppe,  $(G, \ \cdot)$  eine multiplikative.

• Ein  "algebraischer Ring"  kennzeichnet eine Menge  $R = \{0, \, 1, \hspace{0.05cm}\text{...} \hspace{0.1cm} , \ q-1\}$  zusammen mit zwei darin definierten Rechenoperationen,  nämlich der Addition   („$+$”)   und der Multiplikation   („$\hspace{0.05cm}\cdot\hspace{0.05cm}$”).

• Ein  "algebraischer Körper"  ist ein Ring,  bei dem zusätzlich die Division erlaubt ist und das Kommutativgesetz erfüllt wird.

Da wir hier ausschließlich endliche Mengen betrachten,  ist ein Körper  (englisch:  "Field")  gleichzeitig ein  "Galoisfeld"  ${\rm GF}(q)$  der Ordnung  $q$.

Eine wesentliche Eigenschaft des Galoisfeldes  ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm}\text{...} \hspace{0.1cm} , \hspace{0.1cm}z_{q-1}\}$  ist,  dass es mindestens ein primitives Element besitzt.  Ein Element  $z_i ≠ 0$  bezeichnet man dann als  "primitiv",  wenn die folgende Bedingung erfüllt ist  $(k$  ist ganzzahlig$)$:

$$z_i^k \hspace{0.15cm}{\rm mod}\hspace{0.15cm}q = \left\{ \begin{array}{c} \ne 1\\ 1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm}1 \le k < q-1 \\ {\rm f\ddot{u}r} \hspace{0.15cm}k = q-1 \\ \end{array} \hspace{0.35cm} \Rightarrow \hspace{0.35cm} z_i \hspace{0.15cm}{\rm ist \hspace{0.15cm}ein\hspace{0.15cm} primitives \hspace{0.15cm}Element} \hspace{0.05cm}.$$

Nur bei einem primitiven Element   $z_i$   ergeben sich durch die Rechenoparation  $z_i^k$  $($mit  $k = 1, \, 2, \, 3, \, \hspace{0.05cm}\text{...} )$  alle Elemente des Galoisfeldes mit Ausnahme des Nullelementes  $z_0 = 0$.

Hinweise:

• Die Aufgabe behandelt das Themengebiet des Kapitels  "Einige Grundlagen der Algebra".

• Beachten Sie,  dass bei Gruppe, Ring und Körper mit jeweils  $q$  Elementen die Rechenoperationen  „$+$”  und  „$\hspace{0.05cm}\cdot\hspace{0.05cm}$”  jeweils modulo  $q$  zu verstehen sind.

Fragebogen

1

Welche der angegebenen Tabellen beschreiben eine  Gruppe?

	Tabelle  $\rm A3$,
	Tabelle  $\rm M3$,
	Tabelle  $\rm A3$  und Tabelle  $\rm M3$  gemeinsam,
	Tabelle  $\rm A4$  und Tabelle  $\rm M4$  gemeinsam.

2

Welche der angegebenen Tabellen beschreiben einen  Ring?

	Tabelle  $\rm A3$,
	Tabelle  $\rm M3$,
	Tabelle  $\rm A3$  und Tabelle  $\rm M3$  gemeinsam,
	Tabelle  $\rm A4$  und Tabelle  $\rm M4$  gemeinsam,
	Tabelle  $\rm A3$  und Tabelle  $\rm M4$  gemeinsam.

3

Welche der Tabellen beschreiben einen Körper bzw. ein  Galoisfeld?

	Tabelle  $\rm A3$,
	Tabelle  $\rm M3$,
	Tabelle  $\rm A3$  und Tabelle  $\rm M3$  gemeinsam,
	Tabelle  $\rm A4$  und Tabelle  $\rm M4$  gemeinsam.

4

Welche Elemente der Menge  $\{0, \, 1, \, 2\} \ \Rightarrow \ q = 3$  sind  "primitiv"?

	$z_0 = 0$,
	$z_1 = 1$,
	$z_2 = 2.$

5

Welche Elemente der Menge  $\{0, \, 1, \, 2, \, 3\} \ \Rightarrow \ q = 4$  sind  "primitiv"?

	$z_0 = 0$,
	$z_1 = 1$,
	$z_2 = 2$,
	$z_3 = 3$.

Musterlösung

Musterlösung

(1)  Mit der Zahlenmenge  $Z_3 = \{0, \, 1, \, 2\}$  beschreibt

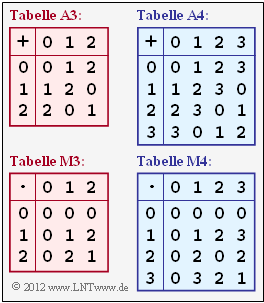
• die Tabelle A3 die additive Gruppe  $(Z_3, \, +)$,
• die Tabelle M3 die multiplikative Gruppe  $(Z_3, \, \cdot)$.

⇒   Lösungsvorschlag 1 und 2.

Die Lösungsvorschläge 3 und 4 treffen dagegen hier nicht zu,  da bei einer Gruppe jeweils nur eine Rechenoperation  (Addition oder Multiplikation)  definiert ist.

(2)  Auf einem algebraischen Ring sind im Gegensatz dazu zwei Rechenoperationen definiert.  Richtig sind somit die  Lösungsvorschläge 3 und 4:

• Die Tabellen A3 und M3 beschreiben gemeinsam den Ring  $(Z_3, \, +, \, \cdot)$.
• Die Tabellen A4 und M4 beschreiben gemeinsam den Ring  $(Z_4, \, +, \, \cdot)$.

Dagegen beschreiben A3 und M4 keinen Ring,  da sie sich auf unterschiedliche Mengen beziehen.

(3)  Jeder Körper ist gleichzeitig auch ein Ring,  aber nicht jeder Ring ist auch ein Körper:

• Bei letzterem ist auch die Division definiert und es gibt für jedes Element auch die  multiplikative Inverse.

• Ein  endlicher Zahlenring  der Ordnung  $q$  (also mit  $q$  Elementen) ist nur dann ein Körper,  wenn  $q$  eine Primzahl ist.

• Man spricht dann auch von einem  Galoisfeld  ${\rm GF}(q)$.

Richtig ist also die Antwort 3:

• Die Rechenoperationen gemäß den Tabellen A3 und M3 ergeben zusammen das Galoisfeld  ${\rm GF}(3)$.
• Dagegen führen die Tabellen A4 (Addition) und M4 Multiplikation) zusammen mit der Menge  $\{0, \, 1, \, 2, \, 3\}$  nicht zum Galoisfeld  ${\rm GF}(4)$.
• Eine Bedingung für ein Galoisfeld ist,  dass es für jedes Element  $z_i$  eine multiplikative Inverse  ${\rm Inv}_{\rm M}{(z_i)}$  gibt,  so dass die Gleichung  $z_i \cdot {\rm Inv}_{\rm M}(z_i) = 1$  erfüllt ist.
• Nach Tabelle M4 existiert  $\rm Inv_M(2)$  aber nicht.  In der dritten Zeile gibt es keine  „$1$”.
• Ein Galoisfeld $\rm GF(4)$ ergibt sich zum Beispiel durch Erweiterung der binären Menge  $\{0, \, 1\}$  zur Menge  $\{0, \, 1, \, \alpha, \, 1+\alpha\}$.  Genaueres hierzu finden Sie auf der Seite "Beispiel eines Erweiterungskörpers".

(4)  Das Nullelement ist nie ein primitives Element.  Auch  $z_1 = 1$  ist kein primitives Element,  denn dann müsste mit  $q = 3$  gelten:

$$z_1^1 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} \ne 1 \hspace{0.05cm},\hspace{0.3cm}z_1^2 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 1 \hspace{0.05cm}.$$

Dagegen ist  $z_2 = 2$  ein primitives Element wegen

$$2^1 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 2 \hspace{0.05cm},\hspace{0.3cm}2^2 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 1 \hspace{0.05cm}.$$

Richtig ist also der  Lösungsvorschlag 3.

(5)  Die Menge  $\{0, \, 1, \, 2, \, 3\}$  besitzt  kein primitives Element  und erfüllt dementsprechend auch nicht die Erfordernisse eines Galoisfeldes:

$$z_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\text{:}\hspace{0.35cm} 1^1 = 1\hspace{0.05cm},\hspace{0.1cm}1^2 = 1\hspace{0.05cm},\hspace{0.1cm}1^3 = 1\hspace{0.05cm},$$

$$z_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\text{:}\hspace{0.35cm} 2^1 = 2\hspace{0.05cm},\hspace{0.1cm}2^2 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 0 \hspace{0.05cm},\hspace{0.1cm}2^3 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 0\hspace{0.05cm},$$

$$z_3 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\text{:}\hspace{0.35cm} 3^1 = 3\hspace{0.05cm},\hspace{0.1cm}3^2 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 1 \hspace{0.05cm},\hspace{0.1cm}3^3 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 3\hspace{0.05cm}.$$