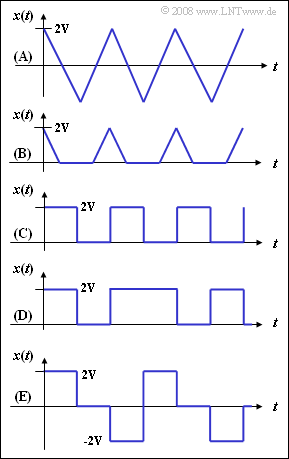
Aufgabe 2.1Z: Signalverläufe

• Zurück zum Buch

Wertdiskret oder wertkontinuierlich?

Rechts sind fünf Signalverläufe dargestellt.  Die ersten drei Signale  $\rm (A)$,  $\rm (B)$  und  $\rm (C)$  sind periodisch und damit auch deterministisch, die beiden unteren Signale haben stochastischen Charakter.

Der Momentanwert dieser Signale  $x(t)$  wird jeweils als eine Zufallsgröße aufgefasst.  Im Einzelnen sind dargestellt:

$\rm (A)$:   ein dreieckförmiges periodisches Signal,

$\rm (B)$:   das Signal  $\rm (A)$  nach Einweggleichrichtung,

$\rm (C)$:   ein rechteckförmiges periodisches Signal,

$\rm (D)$:   ein rechteckförmiges Zufallssignal,

$\rm (E)$:   das Zufallssignal  $\rm (D)$  nach  AMI-Codierung;  
            hierbei bleibt die „Null” erhalten, während eine jede „Eins” alternierend mit   $+2\hspace{0.03cm}\rm V$  und   $-2\hspace{0.03cm} \rm V$   codiert wird.

Hinweis:

• Die Aufgabe gehört zum Kapitel  Vom Zufallsexperiment zur Zufallsgröße.

Fragebogen

1

Bei welchen Signalen beschreibt der Momentanwert eine diskrete Zufallsgröße?
Überlegen Sie sich auch die jeweilige Stufenzahl  $M$.

	Signal $\rm (A)$,
	Signal $\rm (B)$,
	Signal $\rm (C)$,
	Signal $\rm (D)$,
	Signal $\rm (E)$.

2

Bei welchen Signalen ist der Momentanwert eine  (ausschließlich)  kontinuierliche Zufallsgröße?

	Signal $\rm (A)$,
	Signal $\rm (B)$,
	Signal $\rm (C)$,
	Signal $\rm (D)$,
	Signal $\rm (E)$.

3

Welche Zufallsgrößen besitzen einen diskreten und einen kontinuierlichen Anteil?

	Signal $\rm (A)$,
	Signal $\rm (B)$,
	Signal $\rm (C)$,
	Signal $\rm (D)$,
	Signal $\rm (E)$.

4

Für das Signal  $\rm (D)$  wird die relative Häufigkeit  $h_0$  empirisch über  $100\hspace{0.03cm}000$  Binärsymbole ermittelt.
Benennen Sie eine untere Schranke für die Wahrscheinlichkeit,  dass der ermittelte Wert zwischen  $0.49$  und  $0.51$  liegt?

${\rm Min\big[\ Pr(0.49}≤h_0≤0.51)\ \big] \ = \ $  $\%$

5

Wieviele Symbole  $(N_\min)$  müsste man für diese Untersuchung heranziehen,  damit sichergestellt wird,
dass die Wahrscheinlichkeit für das Ereignis  „Die so ermittelte Häufigkeit liegt zwischen  $0.499$  und  $0.501$”  größer als  $99\%$  ist?

$N_\min \ = \ $ $\ \cdot 10^9$

Musterlösung

Musterlösung

(1)  Richtig sind die  Lösungsvorschläge 3, 4 und 5:

• Die Zufallsgrößen  $\rm (C)$  und  $\rm (D)$  sind binär  $(M= 2)$,
• während die Zufallsgröße  $\rm (E)$  dreiwertig ist   $(M= 3)$.

(2)  Richtig ist allein der  Lösungsvorschlag 1:

• Die Zufallsgröße  $\rm (A)$  ist wertkontinuierlich und kann alle Werte zwischen  $\pm 2 \hspace{0.03cm} \rm V$  mit gleicher Wahrscheinlichkeit annehmen.
• Alle anderen Zufallsgrößen sind wertdiskret.

(3)  Richtig ist allein der  Lösungsvorschlag 2:

• Nur die Zufallsgröße  $\rm (B)$  hat einen diskreten Anteil bei  $0\hspace{0.03cm}\rm V$  und
• außerdem noch eine kontinuierliche Komponente  (zwischen  $0\hspace{0.03cm} \rm V$  und  $+2\hspace{0.03cm}\rm V)$.

(4)  Nach dem Bernoullischen Gesetz der großen Zahlen gilt:

$$\rm Pr\left(|\it h_{\rm 0} - \it p_{\rm 0}|\ge\it\varepsilon\right)\le\frac{\rm 1}{\rm 4\cdot \it N\cdot\it\varepsilon^{\rm 2}} = {\it p}_{\rm \hspace{0.01cm}Bernouilli}.$$

• Damit ist die Wahrscheinlichkeit,  dass die relative Häufigkeit  $h_0$  von der Wahrscheinlichkeit  $p_0 = 0.5$  betragsmäßig um mehr als  $0.01$  abweicht,  mit $\varepsilon = 0.01$ berechenbar:

$${\it p}_{\rm \hspace{0.01cm}Bernoulli} = \rm\frac{1}{4\cdot 100000\cdot 0.01^2}=\rm 2.5\% \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\rm Min}\big[({\rm Pr}(0.49 \le h_0 \le 0.51)\big] \hspace{0.15cm}\underline{= 97.5\%}.$$

(5)  Mit  $p_{\rm Bernoulli} = 1 - 0.99 = 0.01$  und  $\varepsilon = 0.001$  gilt wiederum nach dem Gesetz der großen Zahlen:

$${\it p}_{\rm \hspace{0.01cm}Bernoulli}\le\frac{\rm 1}{\rm 4\cdot \it N\cdot\it \varepsilon^{\rm 2}}.$$

• Aufgelöst nach  $N$  erhält man:

$$N\ge\frac{\rm 1}{\rm 4\cdot\it p_{\rm \hspace{0.01cm}Bernoulli}\cdot\it\varepsilon^{\rm 2}}=\rm \frac{1}{4\cdot 0.01\cdot 0.001^{2}}=\rm 0.25\cdot 10^8 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\it N}_{\rm min} \hspace{0.15cm}\underline{= 2.5\cdot 10^9}.$$