Aufgabe 3.2: GSM–Datenraten

• Zurück zum Buch

Blockschaltbild von GSM

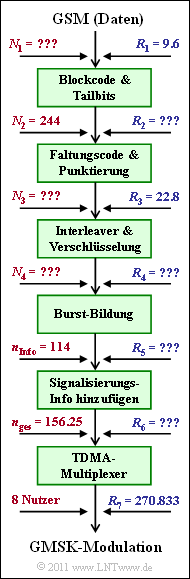
In dieser Aufgabe wird die Datenübertragung bei GSM betrachtet.  Da dieses System jedoch vorwiegend für die Sprachübertragung spezifiziert wurde, benutzen wir bei den folgenden Rechnungen meist die Dauer  $T_{\rm R} = 20 \ \rm ms$  eines Sprachrahmens als zeitliche Bezugsgröße.  Die Eingangsdatenrate beträgt  $R_{1} = 9.6 \ \rm kbit/s$.  Die Anzahl der Eingangsbit in jedem  $T_{\rm R}$–Rahmen sei  $N_{1}$.  Alle in der Grafik mit „$\rm ???$” beschrifteten Kenngrößen sollen in der Aufgabe berechnet werden.

Als erste Blöcke erkennt man in der dargestellten Übertragungskette:

• den äußeren Coder  (Blockcode inklusive vier Tailbits)  mit  $N_{2} = 244 \ \rm Bit$  pro Rahmen  $(T_{\rm R} = 20 \ \rm ms)$   ⇒   Rate  $R_{2}$  ist zu ermitteln,
• den Faltungscoder mit der Coderate  $1/2$, und anschließender Punktierung  $($Verzicht auf  $N_{\rm P} \ \rm Bit)$    ⇒   Rate $R_{3} = 22.8 \ \rm kbit/s$,
• Interleaving und Verschlüsselung, beides ratenneutral.  Am Ausgang dieses Blockes tritt die Rate  $R_4$  auf.

Die weitere Signalverarbeitung sieht prinzipiell wie folgt aus:

• Jeweils  $114$  (codierte, verwürfelte, verschlüsselte) Datenbit werden zusammen mit  $34$  Kontrollbit (für Trainingsfolge, Tailbits, Guard Period) und einer Pause  $($Dauer:   $8.25 \ \rm Bit)$  zu einem so genannten  "Normal Burst"  zusammengefasst.  Die Rate am Ausgang wird mit  $R_{5}$  bezeichnet.
• Zusätzlich werden weitere Bursts  (Frequency Correction Burst, Synchronisation Burst, Dummy Burst, Access Bursts)  zur Signalisierung hinzugefügt.  Die Rate nach diesem Block ist  $R_{6}$.
• Schließlich folgt noch die TDMA–Multiplexeinrichtung, so dass die Gesamtbruttodatenrate des GSM gleich  $R_{\rm ges} = R_{7}$  beträgt.

Als bekannt vorausgesetzt wird die Gesamtbruttodatenrate  $R_{\rm ges} = 270.833 \ \rm kbit/s$  (bei acht Nutzern).

Hinweise:

• Die Aufgabe gehört zum Kapitel  Gemeinsamkeiten von GSM und UMTS.
• Obige Grafik fasst die vorliegende Beschreibung zusammen und definiert die verwendeten Datenraten.
• Alle Raten sind in „$\rm kbit/s$” angegeben.
• $N_{1},  N_{2},  N_{3}$  und  $N_{4}$  bezeichnen die jeweilige Bitanzahl an den entsprechenden Punkten des obigen Blockschaltbildes innerhalb eines Zeitrahmens der Dauer  $T_{\rm R} = 20 \ \rm ms$.
• $N_{\rm ges} = 156.25$  ist die Bitanzahl nach Burst–Bildung, bezogen auf die Dauer  $T_{\rm Z}$  eines TDMA–Zeitschlitzes.
• Davon sind  $N_{\rm Info} = 114$  Informationsbits inklusive Kanalcodierung.

Fragebogen

1

Wie viele Bit werden von der Quelle in jedem Rahmen bereitgestellt?

$N_{1} \ = \ $ $\ \rm Bit$

2

Wie groß ist die Datenrate nach dem äußeren Coder?

$R_{2} \ = \ $ $\ \rm kbit/s$

3

Wie viele Bit würde der Faltungscoder allein (ohne Punktierung) abgeben?

$N_{3}\hspace{0.01cm}' \ = \ $ $\ \rm Bit$

4

Wie viele Bit gibt der punktierte Faltungscoder tatsächlich ab?

$N_{3} \ = \ $ $\ \rm Bit$

5

Wie groß ist die Datenrate nach Interleaver und Verschlüsselung?

$R_{4} \ = \ $ $\ \rm kbit/s$

6

Wie lange dauert ein Zeitschlitz (Time–Slot)?

$T_{\rm Z} \ = \ $ $\ \rm µ s$

7

Wie groß ist die Bruttodatenrate für jeden einzelnen TDMA–Nutzer?

$R_{6} \ = \ $ $\ \rm kbit/s$

8

Welche Bruttodatenrate ergäbe sich ohne Signalisierungsbits?

$R_{5} \ = \ $ $\ \rm kbit/s$

Musterlösung

Musterlösung

(1)  Es gilt  $N_{1} = R_{1} \cdot T_{\rm R} = 9.6 {\ \rm kbit/s} \cdot 20 {\ \rm ms} \hspace{0.15cm} \underline{= 192 \ \rm Bit}$.

(2)  Analog zur Teilaufgabe  (1)  gilt:

$$R_2= \frac{N_2}{T_{\rm R}} = \frac{244\,{\rm Bit}}{20\,{\rm ms}}\hspace{0.15cm} \underline { = 12.2\,{\rm kbit/s}}\hspace{0.05cm}.$$

Beachten Sie bitte:   Bei einer redundanzfreien Binärquelle  (aber nur bei dieser)  besteht kein Unterschied zwischen „$\rm Bit$” und „$\rm bit$”.

(3)  Der Faltungscoder der Rate  $1/2$  allein würde aus seinen  $N_{2} = 244$  Eingangsbits genau  $N_{3}\hspace{0.01cm}' \hspace{0.15cm}\underline{= 488}$  Ausgangsbits pro Rahmen generieren.

(4)  Aus der angegebenen Datenrate  $R_{3} = 22.8 \ \rm kbit/s$  folgt dagegen  $N_{3} \hspace{0.15cm}\underline{= 456}$.

• Das bedeutet, dass von den  $N_{3}' = 488 \ \rm Bit$  durch die Punktierung  $N_{\rm P} = 32 \ \rm Bit$  entfernt werden.

(5)  Sowohl das Interleaving als auch die Verschlüsselung erfolgt sozusagen „datenneutral”.  Damit gilt:

$$R_{4} = R_{3} \hspace{0.15cm}\underline{= 22.8 \ {\rm kbit/s}} \Rightarrow N_{4} = N_{3} = 456.$$

(6)  Für die Bitdauer gilt  $T_{\rm B} = 1/R_{7} = 1/(0.270833 {\ \rm Mbit/s}) \approx 3.69 \ \rm µ s$.

• In jedem Zeitschlitz der Dauer  $T_{\rm Z}$  wird ein Burst – bestehend aus  $156.25 \ \rm Bit$  – übertragen.
• Daraus ergibt sich  $T_{\rm Z} \hspace{0.15cm}\underline{= 576.9 \ \rm µ s}$.

(7)  Bei GSM gibt es acht Zeitschlitze, wobei jedem Nutzer periodisch ein Zeitschlitz zugewiesen wird.

• Damit beträgt die Bruttodatenrate für jeden Nutzer  $R_{6} = R_{7}/8 \hspace{0.15cm}\underline{ \approx 33.854 \ \rm kbit/s}$.

(8)  Berücksichtigt man, dass beim Normal Burst der Anteil der Nutzdaten (inklusive Kanalcodierung)  $114/156.25$  beträgt, so wäre die Rate ohne Berücksichtigung der zugefügten Signalisierungsbits:

$$R_5 = \frac{n_{\rm ges} }{n_{\rm Info} } \cdot R_4 = \frac{156.25 }{114} \cdot 22.8\,{\rm kbit/s}\hspace{0.15cm} \underline { = 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$

• Zum gleichen Ergebnis kommt man, wenn man berücksichtigt, dass bei GSM jeder 13. Rahmen für  Common Control  (Signalisierungs–Info)  reserviert ist:

$$R_5 = \frac{12 }{13 } \cdot 33.854\,{\rm kbit/s} ={ 31.250\,{\rm kbit/s}}\hspace{0.05cm}.$$

• Damit beträgt der prozentuale Anteil der Signalisierungsbits:

$$\alpha_{\rm SB} = \frac{33.854 - 31.250}{33.854 } { \approx 7.7\%}\hspace{0.05cm}.$$