Aufgabe 3.3: Entropie von Ternärgrößen
Aus LNTwww
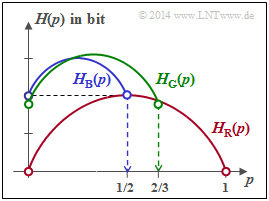
Rechts sehen Sie die Funktionen HR(p), HB(p) und HG(p), wobei R für „Rot” steht, B für „Blau” und G für „Grün”.
Die Wahrscheinlichkeitsfunktionen lauten für alle Zufallsgrößen:
- PX(X)=[p1, p2, p3]⇒|X|=3.
Für den Fragebogen gilt der Zusammenhang p1=p und p2=1−p3−p.
Die Wahrscheinlichkeitsfunktion einer Zufallsgröße
- X={x1,x2,...,xμ,...,xM}
mit dem Symbolumfang |X|=M lautet allgemein:
- PX(X)=[p1,p2,...,pμ,...,pM].
Die Entropie (Unsicherheit) dieser Zufallsgröße berechnet sich entsprechend der Gleichung
- H(X)=E[log21/PX(X)],
und liegt stets im Bereich 0≤H(X)≤log2|X|.
- Die untere Schranke H(X)=0 ergibt sich, wenn eine beliebige Wahrscheinlichkeit pμ=1 ist und alle anderen Null sind.
- Die obere Schranke soll hier wie in der Vorlesung „Information Theory” von Gerhard Kramer an der TU München hergeleitet werden:
- Durch Erweiterung obiger Gleichung um |X| in Zähler und Nenner erhält man mit log2x=ln(x)/ln(2):
- H(X)=1ln(2)⋅E[ln1|X|⋅PX(X)]+log2|X|.
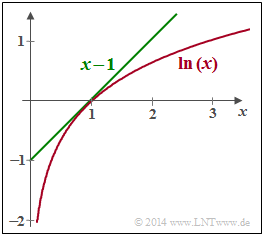
- Wie aus nebenstehender Grafik hervorgeht, gilt die Abschätzung ln(x)≤x−1 mit der Identität für x=1. Somit kann geschrieben werden:
- H(X)≤1ln(2)⋅E[1|X|⋅PX(X)−1]+log2|X|.
- In der Aufgabe 3.2 wurde für den Fall pμ≠0 für alle μ der Erwartungswert E[log21/PX(X)]=|X| berechnet. Damit verschwindet der erste Term und man erhält das bekannte Ergebnis:
- H(X)≤log2|X|.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seite Wahrscheinlichkeitsfunktion und Entropie.
- Ausgegangen wird hier von der gleichen Konstellation wie in der Aufgabe 3.2.
- Die Gleichung der binären Entropiefunktion lautet:
- Hbin(p)=p⋅log21p+(1−p)⋅log211−p.
Fragebogen
Musterlösung
(1) Beide Aussagen sind richtig:
- Setzt man p3=0 und formal p1=p ⇒ p2=1−p, so ergibt sich die binäre Entropiefunktion
- Hbin(p)=p⋅log21p+(1−p)⋅log211−p.
(2) Richtig ist allein der Lösungsvorschlag 1:
- Man kann die binäre Entropiefunktion wegen log(x)=ln(x)/ln(2) auch in die folgende Form bringen:
- Hbin(p)=−1ln(2)⋅[p⋅ln(p)+(1−p)⋅ln(1−p)].
- Die erste Ableitung führt zum Ergebnis
- dHbin(p)dp=−1ln(2)⋅[ln(p)+p⋅1p−ln(1−p)−(1−p)⋅11−p]=1ln(2)⋅[ln(1−p)−ln(p)]=log21−pp.
- Durch Nullsetzen dieser Ableitung erhält man den Abszissenwert p=0.5, der zum Maximum der Entropiefunktion führt:
Hbin(p=0.5)=1 bit ⇒ der Lösungsvorschlag 2 ist falsch. - Durch nochmaliges Differenzieren erhält man für die zweite Ableitung:
- d2Hbin(p)dp2=1ln(2)⋅[−11−p−1p]=−1ln(2)⋅p⋅(1−p).
- Diese Funktion ist im gesamten Definitionsgebiet 0≤p≤1 negativ ⇒ Hbin(p) ist konkav ⇒ der Lösungsvorschlag 1 ist richtig.
(3) Richtig sind hier die Aussagen 1 und 2:
- Für p=0 erhält man die Wahrscheinlichkeitsfunktion PX(X)=[0,1/2,1/2] ⇒ H(X)=1 bit.
- Das Maximum unter der Voraussetzung p3=1/2 ergibt sich für p1=p2=1/4:
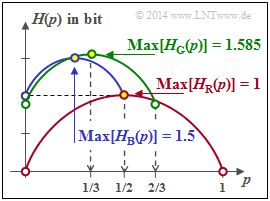
- PX(X)=[1/4,1/4,1/2]⇒Max [HB(p)]=1.5 bit.
- In kompakter Form lässt sich HB(p) mit der Einschränkung 0≤p≤1/2 wie folgt darstellen:
- HB(p)=1.0bit+1/2⋅Hbin(2p).
(4) Richtig sind hier die erste und letzte Aussage:
- Der grüne Kurvenzug beinhaltet mit p=1/3 auch die Gleichverteilung aller Wahrscheinlichkeiten
- Max [HG(p)]=log2(3) bit.
- Allgemein lässt sich der gesamte Kurvenverlauf im Bereich 0≤p≤2/3 wie folgt ausdrücken:
- HG(p)=HG(p=0)+2/3⋅Hbin(3p/2).
- Aus der Grafik auf der Angabenseite erkennt man auch, dass folgende Bedingung erfüllt sein muss:
- HG(p=0)+2/3=log2(3)⇒HG(p=0)=1.585−0.667=0.918bit.
- Der zweite Lösungsvorschlag ist somit falsch. Zum gleichen Ergebnis gelangt man über die Gleichung
- HG(p=0)=1/3⋅log2(3)+2/3⋅log2(3/2)=log2(3)−2/3⋅log2(2).