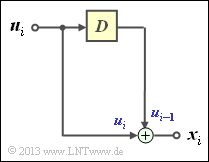
Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js

Aufgabe 3.3Z: Faltung und D–Transformation

Aus LNTwww
Wechseln zu:Navigation, Suche

Vorgegebene Filterstruktur

In dieser Aufgabe beschreiben wir an einem einfachen Beispiel

  • die endliche  Impulsantwort  eines Filters:
g_=(g0,g1,...,gl,...,gm),gl∈GF(2)={0,1},
  • die  Eingangssequenz  des Filters:
u_=(u0,u1,...,ui,...),ui∈GF(2)={0,1},
  • die  Ausgangssequenz  des Filters:
x_=(x0,x1,...,xi,...),xi∈GF(2)={0,1}.

Die Nomenklatur für diese (digitale) Filterbeschreibung haben wir an das Buch „Einführung in die Kanalcodierung” angepasst. In anderen  LNTwww–Büchern bezeichnet oft  x_  den Filtereingang,  y_  den Filterausgang, und die Impulsantwort wird  h  genannt.

Allgemein gilt für die Ausgangssequenz entsprechend der  Faltung  (englisch:  Convolution ):

x_=u_∗g_=(x0,x1,...,xi,...),mitxi=m∑l=0gl⋅ui−l.

Wir repräsentieren nun die Zeitfunktionen  g_, u_  und  x_  durch Polynome in einer Dummy–Variablen  D  und nennen diese die  D–Transformierten:

g_∘−−D−∙G(D) = m∑l=0gl⋅Dl=g0+g1⋅D+g2⋅D2+...+gm⋅Dm,
u_∘−−D−∙U(D) = ∞∑i=0ui⋅Di=u0+u1⋅D+u2⋅D2+...,
x_∘−−D−∙X(D) = ∞∑i=0xi⋅Di=x0+x1⋅D+x2⋅D2+....

Damit wird aus der (komplizierteren) Faltung eine Multiplikation:

x_=u_∗g_∘−−D−∙X(D)=U(D)⋅G(D).

Formal lässt sich dieser Zusammenhang wie folgt nachweisen:

X(D) = ∞∑i=0xi⋅Di=∞∑i=0m∑l=0gl⋅ui−l⋅Di=m∑l=0gl⋅∞∑j=−luj⋅Dj+l=m∑l=0gl⋅Dl⋅∞∑j=0uj⋅Dj
⇒X(D)=U(D)⋅G(D).

Hierbei wurde berücksichtigt, dass alle  uj  für  j<0  nicht existieren und zu Null gesetzt werden können.

Beide Vorgehensweisen zur Berechnung der Ausgangssequenz  x_, nämlich

  • über die Faltung
  • mit Hilfe der D–Transformation,


sollen für das oben skizzierte Digitale Filter demonstriert werden.




Hinweise:

1+D+D2+D3+...=11+D.



Fragebogen

1

Wie lauten die vorliegenden Filterkoeffizienten?

g0 = 
g1 = 
g2 = 

2

Die Sequenz  u_=(1,0,0,1)  sei endlich. Wie lautet die Ausgangssequenz?

x_=(1,0,0,...).
x_=(1,0,0,1,0,0,...).
x_=(1,1,0,1,1,0,0,...).
x_=(1,1,1,1,...)   ⇒   „Dauer–Einsfolge”.

3

Die Sequenz  u_=(1,1,1)  sei endlich. Wie lautet die Ausgangssequenz?

x_=(1,0,0,...).
x_=(1,0,0,1,0,0,...).
x_=(1,1,0,1,1,0,0,...).
x_=(1,1,1,1,...)   ⇒   „Dauer–Einsfolge”.

4

Wie lautet die Ausgangssequenz für  u_=(1,1,1,1,....)   ⇒   „Dauer–Einsfolge”?

x_=(1,0,0,...).
x_=(1,0,0,1,0,0,...).
x_=(1,1,0,1,1,0,0,...).
x_=(1,1,1,1,...)   ⇒   „Dauer–Einsfolge”.

5

Für welchen Vektor  u_  tritt am Ausgang die Folge  x_=(1,1,1,1, ...)  auf?

u_=(1,1,1,1,...)   ⇒   „Dauer–Einsfolge”
u_=(1,0,1,0,1,0,...)   ⇒   alternierende Folge, beginnend mit 1.
u_=(0,1,0,1,0,1,...)   ⇒   alternierende Folge, beginnend mit 0.


Musterlösung

Musterlösung

(1)  Die beiden einzigen von 0 verschiedenen Filterkoeffizienten sind g0 =1_ und g1 =1_.

  • Daraus folgt g2 =0_ und für die D–Transformierte der Impulsantwort:
g_=(1,1)∘−−D−∙G(D)=1+D.


(2)  Die Impulsantwort des betrachteten Filters ist g_=(1,1,0,0,...).

  • Für die Ausgangssequenz erhält man deshalb das Faltungsprodukt
x_ = u_∗g_=(1,0,0,1,0,0,...)∗(1,1,0,0,...)=(1,1,0,1,1,0,...).
  • Zum gleichen Ergebnis kommt man über die D–Transformierten U(D)=1+D3 und G(D)=1+D:
X(D)=U(D)⋅G(D)=(1+D3)⋅(1+D)=1+D+D3+D4.
  • Die Rücktransformation führt wieder zum Ergebnis x_=(1,1,0,1,1,0,0,...)  ⇒  Lösungsvorschlag 3.


(3)  Hier verwenden wir sofort den Weg über die D–Transformierten:

X(D)=(1+D+D2)⋅(1+D)=1+D+D+D2+D2+D3=1+D3⇒x_=(1,0,0,1,0,0,...).
  • Das Ergebnis entspricht dem Lösungsvorschlag 2. Die folgende Berechnung soll den Weg im Zeitbereich veranschaulichen:
(1,0,0,0,0,...)∗(1,1,0,0,...) = (1,1,0,0,0,0,...),
(0,1,0,0,0,...)∗(1,1,0,0,...) = (0,1,1,0,0,0,...),
(0,0,1,0,0,...)∗(1,1,0,0,...) = (0,0,1,1,0,0,...).
  • Da die Faltung eine lineare Operation ist, ergibt sich im Galoisfeld GF(2) aus der Summation:
(1,1,1,0,0,...)∗(1,1,0,0,...)=(1,0,0,1,0,0,...).
  • Hätte man die Faltung nicht in GF(2), sondern für reelle Zahlen durchgeführt, so hätte man das Ergebnis x_=(1,2,2,1,0,0,...) erhalten.


(4)  Die Musterlösung zur Teilaufgabe (3) lässt bereits vermuten, dass hier der Lösungsvorschlag 1 richtig ist.

  • Der Weg über die D–Transformierten bestätigt dieses Ergebnis:
u_=(1,1,1,1,...)∘−−D−∙U(D)=1+D+D2+D3+....
  • Mit der für Berechnungen in GF(2) gültigen Gleichung
1+D+D2+D3+...=11+D
erhält man weiter:
X(D)=U(D)⋅G(D)=11+D⋅(1+D)=1⇒x_=(1,0,0,...).


(5)  Der Weg über die D–Transformierten führt zum Lösungsvorschlag 2.

  • Für diese alternierende Folge u_, beginnend mit 1, erhält man:
X(D) = 1⋅(1+D)+D2⋅(1+D)+D4⋅(1+D)+...=1+D+D2+D3+D4+D5+...⇒x_=(1,1,1,...).
  • Auch bei direkter Anwendung der Faltung wie in Teilaufgabe (2) kann man dieses Ergebnis ablesen.
  • Mit u_=(0,1,0,1,0,1,...) erhält man dagegen x_=(0,1,1,1,1,1,...).
  • Diese unterscheidet sich von der „Dauer–Einsfolge” nur im ersten Bit. Es ist dann x1=0 statt x1=1.

Abgerufen von „http://www.lntwww.de/index.php?title=Aufgaben:Aufgabe_3.3Z:_Faltung_und_D–Transformation&oldid=27867“
  • Powered by MediaWiki