Aufgabe 3.5: Augenöffnung bei Pseudoternärcodierung

• Zurück zum Buch

Augendiagramme beim AMI– und Duobinärcode

Betrachtet werden drei Nachrichtenübertragungssysteme,  jeweils mit folgenden übereinstimmenden Eigenschaften:

• NRZ–Rechteckimpulse mit der Amplitude  $s_0 = 2 \, {\rm V}$,

• Koaxialkabel mit charakteristischer Kabeldämpfung  $a_* = 40 \, {\rm dB}$,

• AWGN–Rauschen mit der Rauschleistungsdichte  $N_0$,

• Empfangsfilter  $H_{\rm E}(f) = 1/H_{\rm K}(f) \cdot H_{\rm G}(f)$,  bestehend aus einem idealen Kanalentzerrer  $H_{\rm K}(f)^{-1}$  und einem Gaußtiefpass  $H_{\rm G}(f)$  mit der normierten Grenzfrequenz  $f_{\rm G} \cdot T \approx 0.5$.

• Schwellenwertentscheider mit optimalen Entscheiderschwellen und optimalem Detektionszeitpunkt  $T_{\rm D} = 0$.

Die in der Aufgabe zu untersuchenden Systemvarianten unterscheiden sich ausschließlich hinsichtlich des Übertragungscodes:

⇒   Das $\text{System A}$  verwendet ein binäres bipolares redundanzfreies Sendesignal.  Bekannt sind folgende Beschreibungsgrößen:

• Grundimpulswerte  $g_0 = 1.56 \, {\rm V}$,  $g_1 = g_{\rm –1} = 0.22 \, {\rm V}$,  $g_2 = g_{\rm –2} = \, \text{ ...} \, \approx 0$

$$\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{ 2} = g_{0} -g_{1}-g_{-1} = 1.12\,{\rm V} \hspace{0.05cm}.$$

• Rauscheffektivwert  $\sigma_d \approx 0.2 \, {\rm V}$

$$\Rightarrow \hspace{0.3cm}\rho_{\rm U} = \frac{\big[\ddot{o}(T_{\rm D})/2\big]^2}{ \sigma_d^2}\approx 31.36\,{\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \approx 15\,{\rm dB}\hspace{0.05cm}.$$

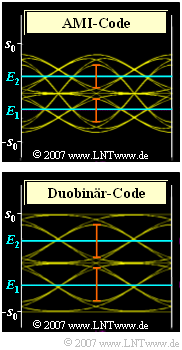
⇒   Das $\text{System B}$  verwendet AMI–Codierung:

• Hier treten die äußeren Symbole  $„+1”$  bzw.  $„–1”$  nur isoliert auf.

• Bei drei aufeinanderfolgenden Symbolen sind unter anderem die Folgen  „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, +1, \, +1, \,\text{ ...}$”  und  „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, 0, \, +1, \, \text{ ...}$”  nicht möglich,

im Gegensatz zur Folge  „$\hspace{-0.1cm}\text{ ...} \, , \, +1, \, –1, \, +1, \, \text{ ...}$”.

⇒   Das $\text{System C}$  verwendet den Duobinärcode:

• Hier wird die alternierende Folge  „$\hspace{-0.1cm} \text{ ...} \, , \, –1, \, +1, \, –1, \, \text{ ...}$”  durch den Code ausgeschlossen,  was sich günstig auf die Augenöffnung auswirkt.

Hinweise:

• Die Aufgabe gehört zum Kapitel  "Impulsinterferenzen bei mehrstufiger Übertragung".

• Nicht alle der hier angegebenen Zahlenwerte sind zur Lösung dieser Aufgabe erforderlich.

Fragebogen

1

Berechnen Sie die halbe Augenöffnung für den  AMI–Code.

$\text{System B:}\hspace{0.4cm} \ddot{o}(T_{\rm D})/2 \ = \ $ $\ {\rm V}$

2

Berechnen Sie den ungünstigsten Störabstand dieses Systems.

$\text{System B:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ $\ {\rm dB}$

3

Wie müssen die Schwellenwerte  $E_1$  und  $E_2$  gewählt werden,  damit das soeben berechnete Ergebnis stimmt?

$E_1 \ \hspace{0.05cm} = \ $ $\ {\rm V}$

$E_2 \ = \ $ $\ {\rm V}$

4

Berechnen Sie die halbe Augenöffnung beim  Duobinär–Code.

$\text{System C:}\hspace{0.4cm} \ddot{o}(T_{\rm D})/2 \ = \ $ $\ {\rm V}$

5

Berechnen Sie den ungünstigsten Störabstand bei der Duobinärcodierung.

$\text{System C:}\hspace{0.4cm} 10 \cdot {\rm lg} \, \rho_{\rm U} \ = \ $ $\ {\rm dB}$

Musterlösung

Musterlösung

(1)  Da beim AMI–Code die Symbolrate gegenüber dem redundanzfreien Binärsystem nicht verändert wird,  bleiben die Grundimpulswerte unverändert:

$$g_0 = 1.56 \, {\rm V}, \ g_1 = g_{\rm –1} = 0.22 \, {\rm V}, \ g_2 = g_{\rm –2} \approx 0.$$

Bei Pseudoternärcodierung gibt es stets zwei Augenöffnungen:

• Die obere Begrenzungslinie des oberen Auges ergibt sich beim AMI–Code wie beim redundanzfreien Binärsystem:

$$d_{\rm oben}= g_0 - 2 \cdot g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm Folge:}-1, +1, -1{\rm )} \hspace{0.05cm}.$$

• Dagegen gilt für die untere Begrenzungslinie des oberen Auges:

$$d_{\rm unten}= g_1 \hspace{0.2cm}{\rm (zugeh\ddot{o}rige} \hspace{0.1cm}{\rm Folgen:}\hspace{0.2cm}0, \hspace{0.05cm}0, +1\hspace{0.2cm}{\rm bzw.}\hspace{0.2cm}+1, \hspace{0.05cm}0, \hspace{0.05cm}0{\rm )}\hspace{0.05cm}.$$

Für die halbe Augenöffnung gilt somit:

$${\ddot{o}(T_{\rm D})}/{2}= {1}/{2} \cdot (d_{\rm oben} - d_{\rm unten}) = {1}/{2} \cdot g_0 - {3}/{2} \cdot g_1 \hspace{0.15cm}\underline {= 0.45\,{\rm V}}\hspace{0.05cm}.$$

Die entsprechende Gleichung für das redundanzfreie Binärsystem lautet:  

$${\ddot{o}(T_{\rm D})}/{2}= g_0 - 2 \cdot g_1 \hspace{0.05cm}.$$

(2)  Bezüglich des Rauschens gibt es keinen Unterschied zwischen den drei Systemen,  da stets die gleiche Symbolrate vorliegt.  Daraus folgt für den AMI–Code:

$$\rho_{\rm U} = \frac{(0.45\,{\rm V})^2}{(0.2\,{\rm V})^2} = 5.06 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 7\,{\rm dB}} \hspace{0.05cm}.$$

• Die Einbuße gegenüber dem redundanzfreien Binärsystem beträgt somit fast  $8 \, {\rm dB}$.

• Der Grund für diesen gravierenden Störabstandverlust ist,  dass beim AMI–Code trotz  $37\%$  Redundanz die bezüglich der Impulsinterferenzen besonders ungünstige Symbolfolge  $\text{ ...} , \, –1, \, +1, \, –1, \text{ ...}$  nicht ausgeschlossen wird.

(3)  Die Schwelle  $E_2$  muss in der Mitte zwischen  $d_{\rm oben}$  und  $d_{\rm unten}$  liegen:

$$E_2= {1}/{2} \cdot (d_{\rm oben} + d_{\rm unten}) = {1}/{2} \cdot (g_0 - g_1 ) \hspace{0.15cm}\underline {= 0.67\,{\rm V}}\hspace{0.05cm}.$$

• Der Schwellenwert  $E_1$  liegt symmetrisch dazu:  $E_1 \, \underline {= \, –0.67 {\rm V}}$.

(4)  Wir gehen wieder von den gleichen Grundimpulswerten aus.

• Die ungünstigste Folge bezüglich der oberen Begrenzungslinie des oberen Auges ist  "$\text{ ...} , 0, \, +1, \, 0, \text{ ...}$",
• während die untere Begrenzungslinie durch  "$\text{ ...} , 0, \, 0, \, +1, \text{ ...}$"  bzw.  "$\text{ ...} , +1, \, 0, \, 0, \text{ ...}$"  bestimmt wird.

• Daraus folgt:

$$d_{\rm oben}= g_0, \hspace{0.2cm} d_{\rm unten} = g_1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\ddot{o}(T_{\rm D})}/{2} = {g_0}/{2} - {g_1}/{2}\hspace{0.15cm}\underline { = 0.667\,{\rm V}} \hspace{0.05cm}.$$

(5)  Mit dem Ergebnis aus  (4)  erhält man analog zur Teilaufgabe  (2):

$$\rho_{\rm U} = \frac{(0.67\,{\rm V})^2}{(0.2\,{\rm V})^2} = 11.2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm U} \hspace{0.15cm}\underline {\approx 10.5\,{\rm dB}} \hspace{0.05cm}.$$

• Voraussetzung für dieses Ergebnis sind Schwellenwerte bei

$$E_2= {1}/{2} \cdot (g_0 + g_1 ) = 0.89\,{\rm V}, \hspace{0.2cm}E_1 = - 0.89\,{\rm V}\hspace{0.05cm}.$$

• Anzumerken ist,  dass hier stets von der gleichen Grenzfrequenz  $f_{\rm G} \cdot T = 0.5$  ausgegangen wurde.

• Bei Optimierung der Grenzfrequenz kann es durchaus sein,  dass der Duobinärcode bei hinreichend großer charakteristischer Kabeldämpfung dem redundanzfreien Binärcode überlegen ist.