Aufgabe 3.8Z: Tupel aus ternären Zufallsgrößen

• Zurück zum Buch

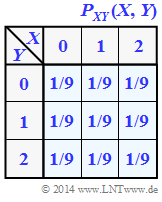
Wir betrachten das Tupel  $Z = (X, Y)$,  wobei die Einzelkomponenten  $X$  und  $Y$  jeweils ternäre Zufallsgrößen darstellen   ⇒   Symbolumfang  $|X| = |Y| = 3$.  Die gemeinsame Wahrscheinlichkeitsfunktion  $P_{ XY }(X, Y)$  ist rechts skizziert.

In dieser Aufgabe sind zu berechnen:

• die Verbundentropie  $H(XY)$  und die Transinformation  $I(X; Y)$,
• die Verbundentropie  $H(XZ)$  und die Transinformation  $I(X; Z)$,
• die beiden bedingten Entropien  $H(Z|X)$  und  $H(X|Z)$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Verschiedene Entropien zweidimensionaler Zufallsgrößen.
• Insbesondere wird Bezug genommen auf die Seiten 
      Bedingte Wahrscheinlichkeit und bedingte Entropie   sowie
     Transinformation zwischen zwei Zufallsgrößen.

Fragebogen

1

Berechnen Sie die folgenden Entropien.

$H(X)\ = \ $ $\ \rm bit$

$H(Y)\ = \ $ $\ \rm bit$

$H(XY)\ = \ $ $\ \rm bit$

2

Welche Transinformation besteht zwischen den Zufallsgrößen  $X$  und  $Y$?

$I(X; Y)\ = \ $ $\ \rm bit$

3

Welche Transinformation besteht zwischen den Zufallsgrößen  $X$  und  $Z$?

$I(X; Z)\ = \ $ $\ \rm bit$

4

Welche bedingten Entropien bestehen zwischen  $X$  und  $Z$?

$H(Z|X)\ = \ $ $\ \rm bit$

$H(X|Z)\ = \ $ $\ \rm bit$

Musterlösung

Musterlösung

(1)  Bei den Zufallsgrößen  $X =\{0,\ 1,\ 2\}$   ⇒   $|X| = 3$  und  $Y = \{0,\ 1,\ 2\}$   ⇒   $|Y| = 3$  liegt jeweils eine Gleichverteilung vor. 

• Damit erhält man für die Entropien:

$$H(X) = {\rm log}_2 \hspace{0.1cm} (3) \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}} \hspace{0.05cm},$$

$$H(Y) = {\rm log}_2 \hspace{0.1cm} (3) \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}}\hspace{0.05cm}.$$

• Die 2D–Zufallsgröße  $XY = \{00,\ 01,\ 02,\ 10,\ 11,\ 12,\ 20,\ 21,\ 22\}$   ⇒   $|XY| = |Z| = 9$  weist ebenfalls gleiche Wahrscheinlichkeiten auf:

$$p_{ 00 } = p_{ 01 } =\text{...} = p_{ 22 } = 1/9.$$

• Daraus folgt:

$$H(XY) = {\rm log}_2 \hspace{0.1cm} (9) \hspace{0.15cm}\underline{= 3.170\,{\rm (bit)}} \hspace{0.05cm}.$$

(2)  Die Zufallsgrößen  $X$  und  $Y$  sind wegen  $P_{ XY }(⋅) = P_X(⋅) · P_Y(⋅)$  statistisch unabhängig.

• Daraus folgt  $I(X, Y)\hspace{0.15cm}\underline{ = 0}$.
• Zum gleichen Ergebnis kommt man über die Gleichung  $I(X; Y) = H(X) + H(Y) - H(XY)$.

Wahrscheinlichkeitsfunktion der 2D-Zufallsgröße  $XZ$

(3)  Interpretiert man  $I(X; Z)$  als die verbleibende Unsicherheit hinsichtlich des Tupels  $Z$,  wenn die erste Komponente  $X$  bekannt ist,  so gilt offensichtlich:

$$I(X; Z) = H(Y)\hspace{0.15cm}\underline{ = 1.585 \ \rm bit}.$$

Rein formal lässt sich diese Aufgabe auch wie folgt lösen:

• Die Entropie  $H(Z)$  ist gleich der Verbundentropie  $H(XY) = 3.170 \ \rm bit$.
• Die Verbundwahrscheinlichkeit  $P_{ XZ }(X, Z)$  beinhaltet neun Elemente der Wahrscheinlichkeit  $1/9$,  alle anderen sind mit Nullen belegt   ⇒   $H(XZ) = \log_2 (9) = 3.170 \ \rm bit$.
• Damit gilt für die Transinformation  $($gemeinsame Information der Zufallsgrößen  $X$  und  $Z)$:

$$I(X;Z) = H(X) + H(Z) - H(XZ) = 1.585 + 3.170- 3.170\hspace{0.15cm} \underline {= 1.585\,{\rm (bit)}} \hspace{0.05cm}.$$

Entropien der 2D-Zufallsgröße  $XZ$

(4)  Entsprechend der zweiten Grafik gilt:

$$H(Z \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(XZ) - H(X) = 3.170-1.585\hspace{0.15cm} \underline {=1.585\ {\rm (bit)}} \hspace{0.05cm},$$

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Z) = H(XZ) - H(Z) = 3.170-3.170\hspace{0.15cm} \underline {=0\ {\rm (bit)}} \hspace{0.05cm}.$$

• $H(Z|X)$  gibt die Restunsicherheit hinsichtlich des Tupels  $Z$  an,  wenn man die erste Komponente  $X$  kennt.
• Die Unsicherheit hinsichtlich des Tupels  $Z$  ist  $H(Z) = 2 · \log_2 (3) \ \rm bit$.
• Bei Kenntnis der Komponente  $X$  halbiert sich die Unsicherheit auf  $H(Z|X) = \log_2 (3)\ \rm bit$.
• $H(X|Z)$  gibt die verbleibende Unsicherheit hinsichtlich der Komponente  $X$  an, wenn man das Tupel  $Z = (X, Y)$  kennt.  Diese Unsicherheit ist natürlich Null:   Kennt man  $Z$, so kennt man auch  $X$.