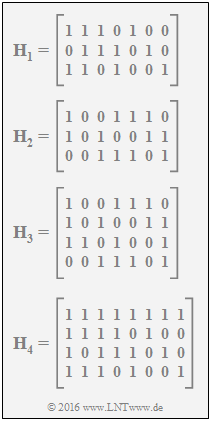
Aufgabe 4.11Z: Coderate aus der Prüfmatrix

• Zurück zum Buch

Vorgegebene Prüfmatrizen

In dieser Aufgabe sollen die Coderaten der Codes  $\mathcal {C}_1, \, \mathcal {C}_2, \, \mathcal {C}_3$  und  $\mathcal {C}_4$  ermittelt werden, wobei die Codes allein durch ihre Prüfmatrizen gegeben sind. Eine untere Schranke für die Coderate  $R$  lautet:

$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.05cm}.$$

Sind die  $m$  Prüfgleichungen aller Matrix–Zeilen linear unabhängig, so gilt in obiger Ungleichung das Gleichheitszeichen.

Verwendet ist hier die folgende Nomenklatur:

• $w_{\rm Z}(j)$  mit  $1 ≤ j ≤ m$  ist das  Hamming–Gewicht  der  $j$–ten Zeile der Prüfmatrix.
• Durch Erwartungswertbildung ergibt sich:

$${\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{m} w_{\rm Z}(j)\hspace{0.05cm}.$$

• Entsprechend gibt  $w_{\rm S}(i)$  mit  $1 ≤ i ≤ n$  das Hamming–Gewicht der  $i$–ten Spalte von  $\mathbf{H}$  an, mit dem Erwartungswert

$${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n} w_{\rm S}(i)\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Grundlegendes zu den Low–density Parity–check Codes.
• Bezug genommen wird insbesondere auf die Seite  Einige Charakteristika der LDPC–Codes.

Fragebogen

1

$\mathbf{H}_1$  beschreibt einen systematischen Code. Wie lauten dessen Parameter?

$n \hspace{0.27cm} = \ $

$k \hspace{0.3cm} = \ $

$m \hspace{0.15cm} = \ $

2

Wie groß ist die Coderate des Codes  $\mathcal {C}_1$  mit der Prüfmatrix  $\mathbf{H}_1$?

$R \ = \ $

3

Wie groß ist die Coderate des Codes  $\mathcal {C}_2$  mit der Prüfmatrix  $\mathbf{H}_2$?

$R \ = \ $

4

Wie groß ist die Coderate des Codes  $\mathcal {C}_3$  mit der Prüfmatrix  $\mathbf{H}_3$?

$R \ = \ $

5

Wie groß ist die Coderate des Codes  $\mathcal {C}_4$  mit der Prüfmatrix  $\mathbf{H}_4$?

$R \ = \ $

Musterlösung

Musterlösung

(1)  Die Matrix $\mathbf{H}_1$ endet mit einer $3 × 3$–Diagonalmatrix.

• Dies ist das Kennzeichen eines systematischen Codes mit $\underline{m = 3}$ Prüfgleichungen.
• Die Codelänge ist $\underline{n = 7}$.
• Damit beinhaltet ein Codewort $\underline{k = 4}$ Informationsbits.

Hinweis: Es handelt sich um den systematischen (7, 4, 3)–Hamming–Code.

(2)  Die Coderate des (7, 4, 3)–Hamming–Codes ist $\underline{R = 4/7 = 0.571}$.

• Das Hamming–Gewicht für alle $m = 3$ Zeilen ist $w_{\rm Z} = 4$ und für das mittlere Hamming–Gewicht über alle Spalten gilt:

$${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n} w_{\rm S}(j) = 1/7 \cdot [2 + 3 + 2+2 + 1+1 +1] = 12/7 \hspace{0.05cm}.$$

• Damit gilt für die angegebene untere Schranke der Coderate:

$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{w_{\rm Z}} = 1 - \frac{12/7}{4}\hspace{0.15cm} \underline{= 4/7 \approx 0.571}\hspace{0.05cm}.$$

• Das bedeutet: Die tatsächliche Coderate ist gleich der unteren Schranke   ⇒   die $m = 3$ Prüfgleichungen von $\mathbf{H}_1$ sind linear unabhängig.

(3)  Die erste Zeile von $\mathbf{H}_2$ ist die Summe aus der ersten Zeile $(z_1)$ und der zweiten Zeile $(z_2)$ von $\mathbf{H}_1$.

• Die zweite Zeile ist gleich $z_2 + z_3$ und die dritte Zeile ist $z_1 + z_3$.
• Es handelt sich um den identischen Code  ⇒  Rate $\underline{R = 4/7 = 0.571}$.
• Weiterhin gilt  $w_{\rm Z} = 4$  und  ${\rm E}[w_{\rm S}] = 1/7 \cdot [0 + 6 \cdot 2] = 12/7$.

(4)  Für diesen Code mit  $n = 7$  (Spaltenzahl) und  $m = 4$  (Zeilenzahl) gilt:

$$w_{\rm Z} = 4\hspace{0.05cm},\hspace{0.3cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n}w_{\rm S}(j) = 1/7 \cdot [3 + 1 + 2 +3+2 + 2+3] = 16/7\hspace{0.3cm} \Rightarrow \hspace{0.3cm} R \ge 1 - \frac{16/7}{4}= 3/7 \hspace{0.05cm}.$$

Das Gleichheitszeichen würde nur bei linear unabhängigen Prüfgleichungen gelten, was hier nicht zutrifft:

• Die dritte Zeile von $\mathbf{H}_3$ wurde von $\mathbf{H}_1$ übernommen.
• Streicht man diese Zeile, so ist $\mathbf{H}_3 = \mathbf{H}_2$ und deshalb gilt ebenfalls: $\ \underline{R = 4/7 = 0.571}$.

(5)  Hier gilt  $n = 7$  und  $m = 4$, sowie

$${\rm E}[w_{\rm S}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/8 \cdot [4 + 3 + 4 + 3 + 3+2 + 2+2] = 23/8\hspace{0.05cm},\hspace{0.8cm} {\rm E}[w_{\rm Z}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/4 \cdot [8 + 5 + 5+5] = 23/4$$

$$\Rightarrow \hspace{0.3cm}R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} = 1 - \frac{23/8}{23/4} = 1/2 \hspace{0.05cm}.$$

• Da alle vier Gleichungen linear unabhängig sind, ist die Coderate gleich der unteren Schranke: $\underline{R = 1/2}$.

Hinweis:   Es handelt sich um den erweiterten (8, 4, 4)–Hamming–Code.