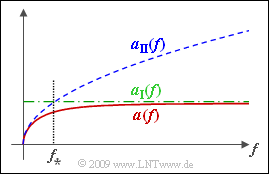
Aufgabe 4.1: Dämpfungsmaß

• Zurück zum Buch

Dämpfungsmaß  $\alpha(f)$  und zwei Schranken für verschiedene Bereiche

Das Dämpfungsmaß  $\alpha(f)$ – sprich „alpha” – einer Leitung gibt die auf die Leitungslänge bezogene Dämpfung an.  Diese Größe ist durch die Leitungsbeläge  $R\hspace{0.05cm}'$,  $L\hspace{0.05cm}'$,  $G\hspace{0.08cm}'$ und  $C\hspace{0.08cm}'$  festgelegt,  wobei die exakte Gleichung etwas kompliziert ist.  Daher wurden zwei leichter handhabbare Näherungen entwickelt:

$$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R\hspace{0.05cm}' \cdot \sqrt{{C\hspace{0.08cm}'}/{ L\hspace{0.05cm}'} } + G\hspace{0.08cm}' \cdot \sqrt{{L\hspace{0.05cm}'}/{ C\hspace{0.08cm}'} }\hspace{0.05cm}\right ] \hspace{0.05cm},$$

$$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{1/2 \cdot \omega \cdot {R\hspace{0.05cm}' \cdot C\hspace{0.08cm}'} }\hspace{0.1cm} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$

Diese beiden Näherungen sind zusammen mit dem tatsächlichen Verlauf  $\alpha(f)$  in der Grafik dargestellt.  Der Schnittpunkt von  $\alpha_{\rm I}(f)$  und  $\alpha_{\rm II}(f)$  ergibt die charakteristische Frequenz  $f_∗$  mit folgender Bedeutung:

• Für  $f \gg f_∗$  gilt  $α(f) ≈ α_{\rm I}(f)$.
• Für  $f \ll f_∗$  gilt  $α(f) ≈ α_{\rm II}(f)$.

Mit diesen Näherungen soll das Dämpfungsmaß  $\alpha(f)$  für ein Nachrichtensignal der Frequenz  $f_0 = 2 \ \rm kHz$  ermittelt werden,  wobei folgende Übertragungsmedien zu betrachten sind:

• ein Kupferkabel mit  $0.6 \ \rm mm$  Durchmesser:

$$R\hspace{0.05cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L\hspace{0.03cm}' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.08cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$

• eine Bronzefreileitung mit  $5 \ \rm mm$  Durchmesser:

$$R\hspace{0.05cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L\hspace{0.03cm}' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.08cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Einige Ergebnisse der Leitungstheorie.

• Die Hinweiseinheit „Neper” (Np) in obigen Gleichungen für  $α_{\rm I}(f)$  und  $α_{\rm II}(f)$  und damit auch für das gesamte Dämpfungsmaß  $α(f)$  ergibt sich aus der Tatsache,  dass der Betragsfrequenzgang als  $|H(f)| = {\rm e}^{-a}$  definiert ist.
• Daraus folgt für die Dämpfung  $a = - {\rm ln} \; |H(f)|$,  wobei der Zusammenhang über den natürlichen Logarithmus durch „Neper” (Np) gekennzeichnet wird.
• Die Einheit des Dämpfungsmaßes  $α = a/l$  ist somit „Np/km”.

Fragebogen

1

Berechnen Sie für das Kupferkabel und das Bronzekabel die angegebene Näherung  $\alpha_{\rm I}$ .

${\rm Kupfer}\hspace{-0.1cm}:\hspace{0.2cm} \alpha_{\rm I} \ = \ $ $\ \rm Np/km$

${\rm Bronze}\hspace{-0.1cm}:\hspace{0.2cm} \alpha_{\rm I} \ = \ $ $\ \rm Np/km$

2

Geben Sie die jeweilige charakteristische Frequenz  $f_*$  an,  die die Gültigkeitsbereiche der beiden Näherungen begrenzt.

${\rm Kupfer}\hspace{-0.1cm}:\hspace{0.2cm} f_* \ = \ $ $\ \rm kHz$

${\rm Bronze}\hspace{-0.1cm}:\hspace{0.2cm} f_* \ = \ $ $\ \rm kHz$

3

Geben Sie unter Zuhilfenahme der beiden Näherungen das Dämpfungsmaß für die Frequenz  $f_0 = 2 \ \rm kHz$  an.

${\rm Kupfer}\hspace{-0.1cm}: \hspace{0.2cm} \alpha (f = f_0) \ = \ $ $\ \rm Np/km$

${\rm Bronze}\hspace{-0.1cm}:\hspace{0.2cm} \alpha (f = f_0) \ = \ $ $\ \rm Np/km$

Musterlösung

Musterlösung

(1)  Für das Kupferkabel gilt mit  $R\hspace{0.03cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 1\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}$:

$${\alpha_{_{\rm I}}(f)} = \frac{1 \,\rm Np/km}{2} \cdot \left [130\,{\rm \Omega} \cdot \sqrt{\frac{35 \cdot 10^{-9}\,{\rm s/\Omega}}{ 0.6 \cdot 10^{-3}\,{\rm \Omega \,s}} } + 10^{-6}\,{\rm \Omega^{-1}} \cdot \sqrt{\frac{0.6 \cdot 10^{-3}\,{\rm \Omega \,s}}{ 35 \cdot 10^{-9}\,{\rm s/\Omega}} }\hspace{0.1cm}\right ]$$

$$\Rightarrow \; \alpha_{\rm I}(f) = 1/2 \cdot \left [130 \cdot 7.638 \cdot 10^{-3}+ 10^{-6} \cdot 0.131 \cdot 10^{3}\right ] {\rm Np/km} \hspace{0.15cm}\underline{= 0.496\,{\rm Np/km}}\hspace{0.05cm}.$$

Für die Bronzeleitung ergibt sich mit  $R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}$:

$$\alpha_{\rm I}(f) = 1/2 \cdot \left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } + 0.5 \cdot 10^{-6} \cdot \sqrt{\frac{ 1.8 \cdot 10^{-3}} {6.7 \cdot 10^{-9}}}\hspace{0.1cm}\right ]$$

$$\Rightarrow \; \alpha_{\rm I}(f) = \frac{1 \,\rm Np/km}{2} \cdot \big [4.244 \cdot 10^{-3}+ 0.259 \cdot 10^{-3}\big ] {\rm Np/km} \hspace{0.15cm}\underline{= 0.0023\,{\rm Np}/{ {\rm km} }}\hspace{0.05cm}.$$

(2)  Die in der Teilaufgabe  (1)  berechnete Schranke  $α_{\rm I}(f)$  gilt nur für  $f \gg f_∗$,  während die Schranke  $α_{\rm II}(f)$  für  $f \ll f_∗$  gültig ist.

• Die charakteristische Frequenz ergibt sich als der Schnittpunkt der beiden Näherungen:

$$\alpha_{\rm II}(f = f_{\star}) = \sqrt{1/2 \cdot \omega_{\star} \cdot R' \cdot C' }\hspace{0.1cm} \bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = \alpha_{\rm I}(f = f_{\star})$$

• Für das Kupferkabel mit  $\text{0.6 mm}$  Durchmesser gilt folgende Bestimmungsgleichung:

$$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= \frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} \hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$

• Dagegen erhält man für die Bronzeleitung mit  $\text{5 mm}$ Durchmesser:

$$f_{\star} = \frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} \hspace{0.15cm}\underline{= 0.109\,{\rm kHz}}\hspace{0.05cm}.$$

(3)  Für das Kupferkabel gilt  $f_0 \ll f_∗$.

• Deshalb ist hier die Näherung  $α_{\rm II}(f)$   ⇒   „starke Dämpfung” zu verwenden:

$$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} \hspace{0.1cm}{\rm Np}/{ {\rm km} } \hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$

• Für die Bronzeleitung ist wegen  $f_0 \gg f_∗$  die Näherung  $α_{\rm I}(f)$   ⇒   „schwache Dämpfung” besser geeignet, siehe Teilaufgabe  (1):

$$\alpha(f = f_0) \hspace{0.15cm}\underline{= 0.0023\hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$