Aufgabe 4.1: Zum „Log Likelihood Ratio”

• Zurück zum Buch

Betrachtete Kanalmodelle

Zur Interpretation von  Log–Likelihood–Verhältnissen  (kurz  $L$–Werten) gehen wir wie im  Theorieteil  vom  Binary Symmetric Channel  (BSC) aus. Die englische Bezeichung ist  Log Likelihood Ratio  (LLR).

Für die binären Zufallsgrößen am Eingang und Ausgang gelte

$$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm}.$$

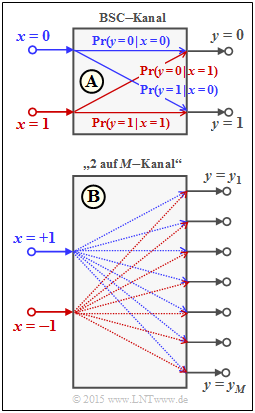
Dieses Modell ist in der oberen Grafik dargestellt. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt:

$${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$

$${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$

Die Verfälschungswahrscheinlichkeit  $\varepsilon$  ist der entscheidende Parameter des BSC–Modells.

Bezüglich der Wahrscheinlichkeitsverteilung am Eingang ist es zweckmäßig, anstelle der Wahrscheinlichkeiten  ${\rm Pr}(x = 0)$  und  ${\rm Pr}(x = 1)$  das  Log Likelihood Ratio  (LLR) zu betrachten.

Für dieses gilt bei der hier verwendeten unipolaren Betrachtungsweise per Definition:

$$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$

wobei der Index  $\rm A$  auf die Apriori–Wahrscheinlichkeit hinweist.

Beispielsweise ergibt sich für  ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$  das Apriori–LLR  $L_{\rm A}(x) = \, -1.382$.

Aus dem BSC–Modell lässt sich zudem der  $L$–Wert der bedingten Wahrscheinlichkeiten  ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$  in Vorwärtsrichtung ermitteln, der in der vorliegenden Aufgabe auch mit  $L_{\rm V}(y)$  bezeichnet wird:

$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = 0, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$

Beispielsweise ergibt sich für  $\varepsilon = 0.1$:

$$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$

Von besonderer Bedeutung für die Codierungstheorie sind die Rückschlusswahrscheinlichkeiten  ${\rm Pr}(x\hspace{0.05cm}|\hspace{0.05cm}y)$, die mit den Vorwärtswahrscheinlichkeiten  ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$  sowie den Eingangswahrscheinlichkeiten  ${\rm Pr}(x = 0)$  und  ${\rm Pr}(x = 1)$  über den Satz von Bayes in Zusammenhang stehen.

Der entsprechende  $L$–Wert wird in dieser Aufgabe  mit $L_{\rm R}(y)$  bezeichnet:

$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Soft–in Soft–out Decoder.
• Bezug genommen wird insbesondere auf die Seite  Zuverlässigkeitsinformation – Log Likelihood Ratio.
• In den letzten Teilaufgaben ist zu klären, ob die gefundenen Zusammenhänge zwischen  $L_{\rm A}, \ L_{\rm V}$  und  $L_{\rm R}$  auch auf den „2–auf–$M$–Kanal” übertragen werden können.
• Hierzu wählen wir für die Eingangssymbole eine bipolare Betrachtungsweise:  „$0$”  →   „$+1$”  sowie  „$1$”   →   „$–1$”.

Fragebogen

1

Wie hängen die bedingten Wahrscheinlichkeiten zweier Zufallsgrößen  $A$  und  $B$  zusammen?

	${\rm Pr}(A\hspace{0.05cm}|\hspace{0.05cm} B) = {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A)$,
	${\rm Pr}(A\hspace{0.05cm}|\hspace{0.05cm}B) = {\rm Pr}(B\hspace{0.05cm}|\hspace{0.05cm} A) \cdot {\rm Pr}(B) / {\rm Pr}(A)$,
	${\rm Pr}(A\hspace{0.05cm}|\hspace{0.05cm} B) = {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm}A) \cdot {\rm Pr}(A) / {\rm Pr}(B)$.

2

Welche Gleichung gilt für den Binärkanal mit den Wahrscheinlichkeiten  ${\rm Pr}(A) = {\rm Pr}(x = 0)$  und  ${\rm Pr}(B) = {\rm Pr}(y = 0)$?

	${\rm Pr}(x = 0 | y = 0) = {\rm Pr}(y = 0 | x = 0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)$,
	${\rm Pr}(x = 0 | y = 0) = {\rm Pr}(y = 0 | x = 0) \cdot {\rm Pr}(y = 0) / {\rm Pr}(x = 0)$.

3

Unter welchen Voraussetzungen gilt für das Rückschluss–LLR für alle möglichen Ausgangswerte  $y ∈ \{0, \, 1\}$:
    $L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x)$  bzw.  $L_{\rm R}(y) = L_{\rm V}(y)$?

	Für jede beliebige Eingangsverteilung  ${\rm Pr}(x = 0), \ {\rm Pr}(x = 1)$.
	Nur für die Gleichverteilung:  $\hspace{0.2cm} {\rm Pr}(x = 0) = {\rm Pr}(x = 1) = 1/2$.

4

Das Ausgangssymbol sei  $y = 1$. Welches Rückschluss–LLR erhält man mit der Verfälschungswahrscheinlichkeit  $\varepsilon = 0.1$  bei gleichwahrscheinlichen Symbolen?

$L_{\rm R}(y = 1) = L(x | y = 1) \ = \ $

5

Das Ausgangssymbol sei nun  $y = 0$. Welches Rückschluss–LLR erhält man für  ${\rm Pr}(x = 0) = 0.2$  und  $\varepsilon = 0.1$?

$L_{\rm R}(y = 0) = L(x | y = 0) \ = \ $

6

Lässt sich das unter (3) hergeleitete Ergebnis   ⇒   $L_{\rm R} = L_{\rm V} + L_{\rm A}$  auch auf den „2–auf–$M$–Kanal” übertragen?

	Ja.
	Nein.

7

Kann man den Zusammenhang auch auf den AWGN–Kanal übertragen?

	Ja.
	Nein.

Musterlösung

Musterlösung

(1)  Für die bedingten Wahrscheinlichkeiten gilt nach dem Satz von Bayes mit der Schnittmenge $A ∩ B$:

$${\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(A)}\hspace{0.05cm}, \hspace{0.3cm} {\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) \cdot \frac{{\rm Pr}(A)}{{\rm Pr}(B)}\hspace{0.05cm}.$$

Richtig ist der Lösungsvorschlag 3. Im Sonderfall ${\rm Pr}(B) = {\rm Pr}(A)$ wäre auch der Vorschlag 1 richtig.

(2)  Mit  $A$  ⇒  „$x = 0$” und  $B$  ⇒  „$y = 0$” ergibt sich sofort die Gleichung gemäß Lösungsvorschlag 1:

$${\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm} y = 0) = {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \cdot \frac{{\rm Pr}(x = 0)}{{\rm Pr}(y = 0)}\hspace{0.05cm}.$$

(3)  Wir berechnen den $L$–Wert der Rückschlusswahrscheinlichkeiten. Unter der Annahme $y = 0$ gilt:

$$L_{\rm R}(y= 0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0)= {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm}y=0)}{{\rm Pr}(x = 1\hspace{0.05cm}|\hspace{0.05cm}y=0)} = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)}{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)\cdot {\rm Pr}(x = 1) / {\rm Pr}(y = 0)}$$

$$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0)= {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)} + {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}$$

$$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = L_{\rm V}(y= 0) + L_{\rm A}(x)\hspace{0.05cm}.$$

In gleicher Weise ergibt sich unter der Annahme $y = 1$:

$$L_{\rm R}(y= 1) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 1) = L_{\rm V}(y= 1) + L_{\rm A}(x)\hspace{0.05cm}.$$

Die beiden Ergebnisse lassen sich mit $y ∈ \{0, \, 1\}$ und

• dem Eingangs–LLR,

$$L_{\rm A}(x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}\hspace{0.05cm},$$

• sowie dem Vorwärts–LLR,

$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = 1)} \hspace{0.05cm},$$

wie folgt zusammenfassen:

$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L_{\rm V}(y) + L_{\rm A}(x)\hspace{0.05cm}.$$

Die Identität $L_{\rm R}(y) ≡ L_{\rm V}(y)$ erfordert $L_{\rm A}(x) = 0$   ⇒   gleichwahrscheinliche Symbole   ⇒   Vorschlag 2.

(4)  Der Aufgabenbeschreibung können Sie entnehmen, dass mit der Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ der Ausgangswert $y = 1$ zum Vorwärts–LLR $L_{\rm V}(y = 1) = \, –2.197$ führt.

• Wegen ${\rm Pr}(x = 0) = 1/2 \ \Rightarrow \ L_{\rm A}(x) = 0$ gilt somit auch:

$$L_{\rm R}(y = 1) = L_{\rm V}(y = 1) \hspace{0.15cm}\underline{= -2.197}\hspace{0.05cm}.$$

(5)  Bei gleicher Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ unterscheidet sich $L_{\rm V}(y = 0)$ von $L_{\rm V}(y = 1)$ nur durch das Vorzeichen.

• Mit ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ L_{\rm A}(x) = \, -1.382$ erhält man somit:

$$L_{\rm R}(y = 0) = (+)2.197 - 1.382 \hspace{0.15cm}\underline{=+0.815}\hspace{0.05cm}.$$

(6)  Wie Sie sicher gerne nachprüfen werden, gilt der Zusammenhang  $L_{\rm R} = L_{\rm V} + L_{\rm A}$  auch für den „2–auf–$M$–Kanal”, unabhängig vom Umfang  $M$  des Ausgangsalphabets   ⇒   Antwort Ja.

(7)  Der AWGN–Kanal wird durch den skizzierten „2–auf–$M$–Kanal” mit  $M → ∞$  ebenfalls beschrieben   ⇒   Antwort Ja.