Aufgabe 4.4: Extrinsische L–Werte beim SPC

• Zurück zum Buch

Geeignete Hilfstabelle

Wir betrachten nochmals den  Single Parity–check Code. Bei einem solchen  ${\rm SPC} \ (n, \, n-1, \, 2)$  stammen von den  $n$  Bit eines Codewortes  $\underline{x}$  die ersten  $k = n -1$  Bit von der Quellenfolge  $\underline{u}$  und es wird nur ein einziges Prüfbit  $p$  hinzugefügt, und zwar derart, dass die Anzahl der Einsen im Codewort geradzahlig ist:

$$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}.$$

Die extrinsische Information über das  $i$–te Codebit wird über alle anderen Symbole  $(j ≠ i)$  gebildet. Deshalb schreiben wir für das um ein Bit kürzere Codewort:

$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}.$$

Der extrinsische  $L$–Wert über das  $i$–te Codesymbol lautet mit dem  Hamming–Gewicht  $w_{\rm H}$  der verkürzten Folge  $\underline{x}^{(-i)}$:

$$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$

• Ist die Wahrscheinlichkeit im Zähler größer als die im Nenner, so ist  $L_{\rm E}(i) > 0$  und damit wird auch der Aposteriori–$L$–Wert  $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$  vergrößert, das heißt tendenziell in Richtung des Symbols  $x_i = 0$  beeinflusst.
• Bei  $L_{\rm E}(i) < 0$  spricht aus Sicht der anderen Symbole  $(j ≠ i)$  vieles dafür, dass  $x_i = 1$  ist.

Behandelt wird ausschließlich der  $\text{SPC (4, 3, 4)}$, wobei für die Wahrscheinlichkeiten  $p_i = {\rm Pr}(x_i = 1)$  gilt:

$$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} p_3 = 0.3 \hspace{0.05cm}, \hspace{0.3cm} p_4 = 0.6 \hspace{0.05cm}.$$

Daraus ergeben sich die Apriori–$L$–Werte zu:

$$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} \right ] \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Soft–in Soft–out Decoder.
• Bezug genommen wird insbesondere auf die Seite  Zur Berechnung der extrinsischen  $L$–Werte.
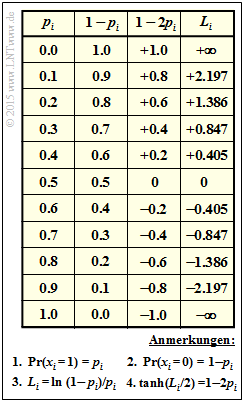
• In der Tabelle sind für  $p_i = 0$  bis  $p_i = 1$  mit Schrittweite $0.1$ (Spalte 1) angegeben:

In Spalte 2:   die Wahrscheinlichkeit  $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$,

in Spalte 3:   die Werte für  $1 - 2p_i$,

in Spalte 4:   die Apriori–$L$–Werte  $L_i = \ln {\big [(1 - p_i)/p_ i \big ]} = L_{\rm A}(i)$.

• Der  Tangens Hyperbolicus  ($\tanh$)  von $L_i/2$  ist identisch mit  $1-2p_i$   ⇒   Spalte 3.
• In der  Aufgabe 4.4Z  wird gezeigt, dass für den extrinsischen  $L$–Wert auch geschrieben werden kann:

$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) \hspace{0.05cm}.$$

Fragebogen

1

Es gelte  $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6$. Berechnen Sie daraus die Apriori–$L$–Werte des  $\text{SPC (4, 3, 4)}$  für Bit 1 und Bit 2.

$L_{\rm A}(i = 1) \ = \ $

$L_{\rm A}(i = 2) \ = \ $

2

Wie lauten die extrinsischen $L$–Werte für Bit 1 und Bit 2.

$L_{\rm E}(i = 1) \ = \ $

$L_{\rm E}(i = 2) \ = \ $

3

Welche Zusammenhänge bestehen zwischen  $p_j$  und  $L_j = L_{\rm A}(j)$?

	Es gilt  $p_j = 1/(1 + {\rm e}^ {L_j})$.
	Es gilt  $1-2p_j = ({\rm e}^ {L_j} - 1) \ / \ ({\rm e}^ {L_j} + 1)$.
	Es gilt  $1-2p_j = \tanh {(L_j/2)}$.

4

Es gelte weiter  $p_1 = 0.2, \ p_2 = 0.9, \ p_3$ und $p_4 = 0.6$. Berechnen Sie die extrinsischen $L$–Werte für Bit 3 und Bit 4.
Verwenden Sie hierzu verschiedene Gleichungen.

$L_{\rm E}(i = 3) \ = \ $

$L_{\rm E}(i = 4) \ = \ $

Musterlösung

Musterlösung

(1)  Für die Apriori–$L$–Werte der beiden ersten Bits des Codewortes gilt:

$$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} \hspace{0.05cm},$$

$$L_{\rm A}(i = 2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_2}{p_2} \right ] = {\rm ln} \hspace{0.1cm} 1/9 \hspace{0.15cm}\underline{= -2.197} \hspace{0.05cm}.$$

Die Werte können aus der vierten Spalte der auf der Angabenseite beigefügten Tabelle abgelesen werden.

(2)  Zur Berechnung des extrinsischen $L$–Wertes über das $i$–te Bit dürfen nur die Informationen über die drei anderen Bits $(j ≠ i)$ herangezogen werden. Mit der angegebenen Gleichung gilt:

$$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} \hspace{0.05cm}.$$

• Für das Produkt erhält man entsprechend der dritten Spalte der Tabelle:

$$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + 0.064}{1 - 0.064} = {\rm ln} \hspace{0.1cm} (1.137)\hspace{0.15cm}\underline{= +0.128} \hspace{0.05cm}.$$

• Hinsichtlich Bit 2 erhält man entsprechend:

$$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.048}{1 +0.048} = {\rm ln} \hspace{0.1cm} (0.908)\hspace{0.15cm}\underline{= -0.096} \hspace{0.05cm}.$$

(3)  Für den Apriori–$L$–Wert gilt:

$$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1-p_j = p_j \cdot {\rm e}^{L_j} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } \hspace{0.05cm} .$$

• Damit gilt auch:

$$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$

• Multipliziert man Zähler und Nenner noch mit ${\rm e}^{-L_j/2}$, so erhält man:

$$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$

• Somit sind alle Lösungsvorschläge richtig.
• Die Funktion Tangens Hyperbolicus findet man zum Beispiel tabellarisch in Formelsammlungen oder in der letzten Spalte der vorne angegebenen Tabelle.

(4)  Wir berechnen $L_{\rm E}(i = 3)$ zunächst in gleicher Weise wie in der Teilaufgabe (2):

$$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.096}{1 -0.096} = {\rm ln} \hspace{0.1cm} (1.212)\hspace{0.15cm}\underline{= +0.193} \hspace{0.05cm}.$$

• Den extrinsischen $L$–Wert hinsichtlich des letzten Bits berechnen wir nach der Gleichung

$$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \hspace{0.05cm}.$$

• Damit ergibt sich entsprechend der obigen Tabelle:

$$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1/2 = +0.693 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_1\hspace{0.05cm},$$

$$p_2 = 0.9 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2 = -2.197 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2/2 = -1.099\hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_2\hspace{0.05cm},$$

$$p_3 = 0.3 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3 = 0.847 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3/2 = +0.419 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$

• Das Endergebnis lautet somit:

$$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 -0.192}{1 +0.192}\hspace{0.15cm}\underline{= -0.389} \hspace{0.05cm}.$$