Aufgabe 4.7: Decodierung von Produktcodes
Wir betrachten wie in der Aufgabe 4.6 einen Produktcode, basierend auf
- dem Hammingcode HC (7, 4, 3) ⇒ C1,
- dem verkürzten Hammingcode HC (6, 3, 3) ⇒ C2.
Die Prüfmatrizen dieser Komponentencodes lauten:
- { \boldsymbol{\rm H}}_1 = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0 \\ 0 &1 &1 &1 &0 &1 &0 \\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm H}}_2 = \begin{pmatrix} 1 &1 &0 &1 &0 &0 \\ 1 &0 &1 &0 &1 &0 \\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.
Der Vollständigkeit halber sind auch die Generatormatrizen angegeben, die jedoch zur Lösung der Aufgabe nicht benötigt werden:
- { \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1 \\ 0 &1 &0 &0 &1 &1 &0 \\ 0 &0 &1 &0 &0 &1 &1 \\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm G}}_2 = \begin{pmatrix} 1 &0 &0 &1 &1 &0 \\ 0 &1 &0 &1 &0 &1 \\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.
Die Hard Decision Decodierung dieses Codes geschieht vorzugsweise iterativ, indem abwechselnd alle Zeilen und anschließend alle Spalten syndromdecodiert werden. Siehe: Iterative Syndromdecodierung von Produktcodes.
Die Syndromdecodierung (eindimensionaler) Blockcodes wurde bereits im Kapitel Decodierung linearer Blockcodes behandelt. Hier eine kurze Zusammenfassung und eine Adaption an den zweidimensionalen Fall:
- Aus dem Empfangswort \underline{y} (einer Zeile bzw. einer Spalte der vorgegebenen Empfangsmatrix) wird das Syndrom entsprechend \underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T} bzw. \underline{s} = \underline{y} \cdot \mathbf{H}_2^{\rm T} gebildet.
- Mit dem Ergebnis \underline{s} = \underline{s}_{\mu} kann man in obigen Tabellen den so genannten Nebenklassenanfüherer \underline{e}_{\mu} ablesen.
- Das korrigierte Codewort ist dann \underline{y} + \underline{e}_{\mu}.
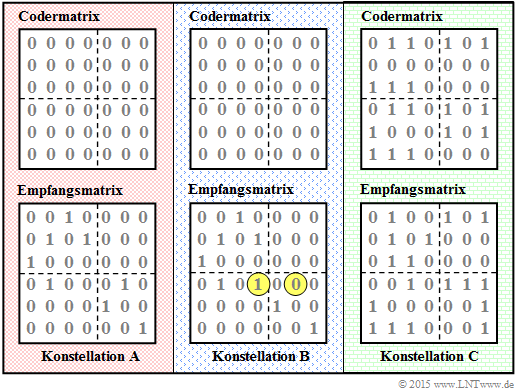
Die nebenstehende Grafik zeigt drei verschiedene Coder– und Empfangsmatrizen, die in den Teilaufgaben (1), (2) und (3) zu analysieren sind:
- Wir benennen diese mit Konstellation \mathbf{A}, \mathbf{B} und \mathbf{C}.
- Gelb markiert sind die Unterschiede der Empfangsmatrix von Konstellation \mathbf{B} gegenüber \mathbf{A}.
- In beiden Fällen besteht die Codermatrix nur aus Nullen.
- Die Codermatrix von \rm C wurde in der Aufgabe 4.6 ermittelt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Grundlegendes zu den Produktcode.
- Bezug genommen wird insbesondere auf die Seite Iterative Syndromdecodierung von Produktcodes.
Fragebogen
Musterlösung
- Die Einzelfehler in den Zeilen 1, 3, 5 und 6 werden vom (7, \ 4, \ 3)–Hammingcode erkannt und können korrigiert werden
⇒ grüne Markierungen in der Grafik „1. Iteration horizontal”. - Für die zweite Zeile ergibt sich das Syndrom
- \underline{s} = \underline{y}_2 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 \\ 1 &1 &0 \\ 0 &1 &1 \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1 \hspace{0.03cm}.
- Nach der oberen Syndromtabelle auf der Angabenseite wird somit fälschlicherweise das letzte Bit „korrigiert”. Fehlkorrekturen sind in der oberen Grafik rot eingetragen.
- Entsprechend gilt für die vierte Zeile:
- \underline{s} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0 \right ) \cdot { \boldsymbol{\rm H}}_1^{\rm T} = \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right )= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \underline{s}_4 \hspace{0.05cm}.
- Dies bewirkt eine Fehlkorrektur von Bit 5.
- Die vertikale Decodierung der Spalten 1, 3, 4, 5, 6 und 7 ist problemlos, da höchstens ein Fehler pro Spalte auftritt, der durch den verkürzten Hammingcode \rm (6, \ 3, \ 3) korrigiert werden kann.
- In Spalte 2 kommt es dagegen zu einer Fehlkorrektur des letzten Bits entsprechend der unteren Syndromtabelle. Mit der Transponierten der \rm (6, \ 3, \ 3)–Prüfmatrix \mathbf{H}_2 ergibt sich nämlich:
- \underline{s}= \underline{y}_{2{\rm S}}\cdot { \boldsymbol{\rm H}}_2^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \begin{pmatrix} 1 &1 &0 \\ 1 &0 &1 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) + \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1.
- Die zweite Horizontaldecodierung ist problemlos, da nun in jeder Zeile maximal ein Fehler auftritt ⇒ Lösungsvorschlag 3.
(2) Die folgende Grafik zeigt den Decodiervorgang entsprechend den Vorgaben gemäß \mathbf{B}.
Trotz nur geringfügigen Modifikationen gegenüber \mathbf{A} gibt es nun gravierende Unterschiede:
- Durch die erste Horizontaldecodierung lauten nun die „korrigierten” Zeilen 2 und 4 gleichermaßen: (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1), das heißt, das letzte Bit dieser Zeilen wird jeweils fehlkorrigiert.
- Die Vertikaldecodierung führt zu gleichlautenden Spalten 2, 4 und 6, nämlich (0, \, 1, \, 0, \, 1, \, 0, \, 1). Danach gibt es in jeder Zeile und in jeder Spalte drei Einsen (oder keine einzige).
- Diese Konstellation bleibt für beliebig weitere (horizontale oder vertikale) Decodierungen erhalten, weil sich für d_{\rm min} = 3 stets das Syndrom \underline{s}_0 = (0, \, 0, \, 0) ergibt.
Richtig ist also der Lösungsvorschlag 5.
(3) Vergleicht man die Coder– und Empfangsmatrizen (Unterschiede sind blau markiert), so kann man entsprechend der folgenden Grafik durch Modulo–2–Additionen die Fehlermatrix erstellen.
Die Fehlermatrix ist gleich der Empfangsmatrix von \mathbf{A} ⇒ auch hier ist der Lösungsvorschlag 3 richtig.