Aufgabe 5.5: Mehrteilnehmer–Interferenzen

$\rm PAKF$ und

$\rm PKKF$ von M–Sequenzen mit

$P = 31$

Wir betrachten die PN–Modulation mit folgenden Parametern:

Die Spreizung erfolgt mit der M–Sequenz mit Oktalkennung $(45)$ , ausgehend vom Grad $G = 5$ . Die Periodenlänge ist somit

$P = 2^5 –1 = 31.$

Der AWGN–Parameter wird mit $10 · \lg \ (E_{\rm B}/N_0) = 5 \ \rm dB$ festgelegt ⇒ $E_{\rm B}/N_0 = 3.162 = 1/0.316$ .
Die Bitfehlerwahrscheinlichkeit beträgt ohne interferierende Teilnehmer im gleichen Frequenzband:

$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2\cdot E_{\rm B}}/{N_{\rm 0}}}\right ) \approx {\rm Q} \left ( \sqrt{2 \cdot 3.162}\right ) = {\rm Q} \left ( 2.515 \right ) \approx 6 \cdot 10^{-3} \hspace{0.05cm}.$

Da ohne interferierende Teilnehmer alle Nutzabtastwerte gleich $±s_0$ sind ("Nyquistsystem"), ist die Bitfehlerwahrscheinlichkeit mit dem Rauscheffektivwert $σ_d$ vor dem Entscheider $($ herrührend vom AWGN–Rauschen $)$ wie folgt gegeben:

$p_{\rm B} = {\rm Q} \left ( {s_0}/{\sigma_d}\right ) \hspace{0.05cm}.$

In dieser Aufgabe soll untersucht werden, wie die Bitfehlerwahrscheinlichkeit durch einen zusätzlichen Teilnehmer verändert wird.

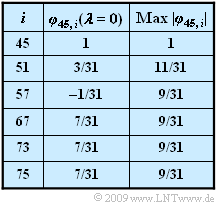
Die möglichen Spreizfolgen des interferierenden Teilnehmers seien ebenfalls durch $P = 31$ festgelegt. Zur Verfügung stehen die PN–Generatoren mit den Oktalkennungen $(45)$ , $(51)$ , $(57)$ , $(67)$ , $(73)$ und $(75)$ .

In der Tabelle sind die PKKF–Werte für $λ = 0$ angegeben, desweiteren auch der jeweilige Maximalwert für eine beliebige Anfangsphase:

${\rm Max}\,\,|{\it \varphi}_{45,\hspace{0.05cm}i}| = \max_{\lambda} \,\,|{\it \varphi}_{45,\hspace{0.05cm}i}(\lambda)| \hspace{0.05cm}.$

Der Sonderfall $φ_\text{45, 45}(λ = 0)$ gibt den PAKF–Wert der Spreizfolge mit der Oktalkennung $(45)$ an.

Im Verlauf dieser Aufgabe und in der Musterlösung werden folgende Signale erwähnt:

$q(t)$ : binäres bipolares Quellensignal, Symboldauer

$T$ ,

$c(t)$ :

$±1$ –Spreizsignal, Chipdauer

$T_c$ ,

$s(t)$ : bandgespreiztes Sendesignal; es gilt

$s(t) = q(t) · c(t)$ , Amplitude

$±s_0$ , Chipdauer

$T_c$ ,

$n(t)$ : AWGN–Rauschen, gekennzeichnet durch den Quotienten

$E_{\rm B}/N_0$ ,

$i(t)$ : Interferenzsignal des störenden Teilnehmers,

$r(t)$ : Empfangssignal; es gilt

$r(t) = s(t) + n(t) + i(t)$ ,

$b(t)$ : bandgestauchtes Signal; es gilt

$b(t)= r(t) · c(t)$ ,

$d(t)$ : Detektionssignal nach Integration von

$b(t)$ über die Symboldauer

$T$ ,

$v(t)$ : Sinkensignal, der Vergleich mit

$q(t)$ liefert die Fehlerwahrscheinlichkeit.

Hinweise:

Die Aufgabe gehört zum Kapitel Fehlerwahrscheinlichkeit der PN-Modulation.
Bezug genommen wird insbesondere auf den Abschnitt Zwei Teilnehmer mit M–Sequenz–Spreizung.
Für die so genannte Q-Funktion kann von folgenden Näherungen ausgegangen werden:

${\rm Q} (2) \approx 0.02275, \hspace{0.2cm}{\rm Q} (3) \approx 0.00135, \hspace{0.2cm}{\rm Q} (5) \approx 2.45 \cdot 10^{-7} \hspace{0.05cm}.$

Fragebogen

$σ_d/s_0 \ = \$

$p_{\rm B}\ = \$

$\ \%$

$p_{\rm B}\ = \$

$\ \%$

	Mit der Oktalkennung $(51)$ ist $p_{\rm B} = 0.1\%$ möglich.
	Mit der Oktalkennung $(57)$ ist $p_{\rm B} = 0.7\%$ möglich.
	Mit der Oktalkennung $(67)$ ist $p_{\rm B} = 1.2\%$ möglich.

Musterlösung

(1) Aus den beiden vorne angegebenen Gleichungen folgt direkt:

$p_{\rm B} = {\rm Q}(2.515) = {\rm Q}({s_0}/{\sigma_d}) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \frac{\sigma_d}{s_0} = \frac{1}{2.515} = 0.398 \hspace{0.15cm}\underline {\approx 0.4} \hspace{0.05cm}.$

Man könnte diese Größe aber auch über die allgemeinere Gleichung

$\sigma_d^2 = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty} |H_{\rm I}(f) |^2 \,\,{\rm d} {\it f}\hspace{0.05cm} = \frac{N_0}{2 }\cdot\int^{+\infty}_{-\infty}{\rm si}^2(\pi f T)\,\,{\rm d} {\it f} = \frac{N_0}{2T } \hspace{0.05cm}$

berechnen. Hierbei beschreibt

$H_{\rm I}(f)$ den Integrator im Frequenzbereich.

Mit $E_{\rm B}= s_0^2 · T$ erhält man das gleiche Ergebnis:

$\frac{\sigma_d^2}{s_0^2} = \frac{N_0}{2 \cdot s_0^2 \cdot T } = \frac{N_0}{2 E_{\rm B} } = \frac{0.316}{2 } = 0.158\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\sigma_d}/{s_0} = 0.398 \approx 0.4 \hspace{0.05cm}.$

(2) Benutzt der interferierende Teilnehmer die gleiche M–Sequenz $(45)$ wie der betrachtete Nutzer,
so sind die (normierten) Detektionsnutzabtastwerte gleich $+2$ $($ zu $25\%)$ , $-2$ $($ zu $25\%)$ und $0$ $($ zu $50\%)$ .

Bei $d(νT) = ±2$ wird die Fehlerwahrscheinlichkeit für den betrachteten Teilnehmer signifikant verkleinert. In diesem Fall übertragen beide Nutzer das gleiche Bit $($ „ $+1$ ” oder „ $-1$ ” $)$ und der Abstand von der Schwelle wird verdoppelt:

$p_{\rm B}\,\,\big [{\rm falls}\,\, d (\nu T) = \pm 2s_0 \big ] = {\rm Q} \left ( 2 \cdot 2.515 \right ) = {\rm Q} \left ( 5.03 \right ) \approx 2.45 \cdot 10^{-7} \approx 0 \hspace{0.05cm}.$

Ist dagegen $d(νT) = 0$ (zum Beispiel, wenn $a_\text{1(s)} = +1$ und $a_\text{1(i)} = -1$ gilt oder umgekehrt), so löschen sich die Signale vollständig aus und man erhält

$p_{\rm B}\,\,\big[{\rm falls}\,\, d (\nu T) = 0 \big] = {\rm Q} \left ( 0 \right ) = 0.5 \hspace{0.05cm}.$

Durch Mittelung über diese beiden gleichwahrscheinlichen Möglichkeiten ergibt sich so für die mittlere Bitfehlerwahrscheinlichkeit:

$p_{\rm B}= 0.5 \cdot 2.45 \cdot 10^{-7}+ 0.5 \cdot 0.5 \hspace{0.15cm}\underline {\approx 25\%} \hspace{0.05cm}.$

(3) Wir betrachten zunächst nur den Nutzanteil ⇒ $n(t) = 0$ , beschränken uns auf das erste Datensymbol und setzen den Koeffizienten $a_\text{1(s)} = +1$ voraus.

Dann gilt innerhalb dieses Datenbits $s(t) = c_{45}(t)$ .
Ist der Koeffizient $a_\text{1(i)}$ des interferierenden Teilnehmers ebenfalls $+1$ , so erhält man für die vorne spezifizierten Signale im Zeitintervall von $0$ bis $T$ :

$r(t) = c_{45}(t) + c_{75}(t)\hspace{0.05cm},$

$b(t) = r(t) \cdot c_{45}(t) = \left [c_{45}(t) + c_{75}(t) \right ] \cdot c_{45}(t) = 1+ c_{45}(t) \cdot c_{75}(t) \hspace{0.05cm},$

$d (T) = \frac{1}{T} \cdot \int_{0 }^{ T} b (t )\hspace{0.1cm} {\rm d}t = 1 + {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$

Hierbei bezeichnet $φ_\text{45, 75}(τ)$ die PKKF zwischen den Spreizfolgen mit den Oktalkennungen $(45)$ und $(75)$ , die in der Tabelle auf der Angabenseite zu finden sind.

Entsprechend gilt für den Detektionsnutzabtastwert unter der Voraussetzung $a_\text{1(s)} = +1$ und $a_\text{1(i)} =-1$ :

$d (T) = 1 - {\it \varphi}_{45,\hspace{0.05cm}75}(\lambda = 0) \hspace{0.05cm}.$

Aus Symmetriegründen liefern die Koeffizienten $a_\text{1(s)} = -1$ , $a_\text{1(i)} = -1$ sowie $a_\text{1(s)} = -1$ , $a_\text{1(i)} = +1$ die genau gleichen Beiträge für die Bitfehlerwahrscheinlichkeit wie $a_\text{1(s)} = +1$ , $a_\text{1(i)} = +1$ bzw. $a_{1(s)} = +1$ , $a_{1(i)} = –1$ , wenn man zudem das AWGN–Rauschen berücksichtigt.

Mit dem Ergebnis der Teilaufgabe (1) und mit $φ_\text{45, 75}(λ = 0) = 7/31$ erhält man somit näherungsweise:

$p_{\rm B} = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1+ 7/31}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{1- 7/31}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( \frac{1.225}{0.4} \right ) + \frac{1}{2} \cdot {\rm Q} \left ( \frac{0.775}{0.4} \right ) = \frac{1}{2} \cdot {\rm Q} \left ( 3.06 \right ) + \frac{1}{2} \cdot {\rm Q} \left ( 1.94 \right )$

$\Rightarrow \hspace{0.3cm} p_{\rm B}\approx \frac{1}{2} \cdot \left [{\rm Q} \left ( 3 \right ) + {\rm Q} \left ( 2 \right ) \right ] = \frac{1}{2} \cdot \left [0.00135 + 0.02275 \right ] \hspace{0.15cm}\underline {= 1.2\%}\hspace{0.05cm}.$

(4) Möglich sind die Lösungsvorschläge 2 und 3:

Der PKKF–Wert $φ_\text{45, 57}(λ = 0)$ ist betragsmäßig nur $1/31$ und damit ist die Fehlerwahrscheinlichkeit nur geringfügig größer als $0.6\%$ .
Die Folge mit den Oktalkennung $(67)$ führt dagegen zur gleichen PKKF wie die Folge $(75)$ .
Ohne störenden Teilnehmer gilt entsprechend dem Angabenblatt: $p_{\rm B} = 0.6\%$ .
Mit Interferenz kann dieser Wert nicht unterschritten werden ⇒ Der Lösungsvorschlag 1 ist nicht möglich.