Grundlagen der codierten Übertragung

Inhaltsverzeichnis

1 # ÜBERBLICK ZUM ZWEITEN HAUPTKAPITEL #
2 Informationsgehalt – Entropie – Redundanz
3 Quellencodierung – Kanalcodierung – Übertragungscodierung
4 Systemmodell und Beschreibungsgrößen
5 AKF–Berechnung eines Digitalsignals
6 LDS–Berechnung eines Digitalsignals
7 AKF und LDS bei bipolaren Binärsignalen
8 AKF und LDS bei unipolaren Binärsignalen
9 Aufgaben zum Kapitel

# ÜBERBLICK ZUM ZWEITEN HAUPTKAPITEL #

Das zweite Hauptkapitel behandelt die so genannte Übertragungscodierung, die in der Literatur manchmal auch als »Leitungscodierung« bezeichnet wird. Dabei wird durch gezieltes Hinzufügen von Redundanz eine Anpassung des digitalen Sendesignals an die Eigenschaften des Übertragungskanals erreicht.

Im Einzelnen werden behandelt:

einige grundlegende Begriffe der Informationstheorie wie »Informationsgehalt« und »Entropie«,
die »Autokorrelationsfunktion« und die »Leistungsdichtespektren« von Digitalsignalen,
die »redundanzfreie Codierung«, die zu einem nichtbinären Sendesignal führt,
die Berechnung von »Symbol– und Bitfehlerwahrscheinlichkeit« bei mehrstufigen Systemen,
die so genannten »4B3T–Codes« als ein wichtiges Beispiel von blockweiser Codierung, und
die »Pseudoternärcodes«, die jeweils eine symbolweise Codierung realisieren.

Die Beschreibung erfolgt durchgehend im Basisband und es werden weiterhin einige vereinfachende Annahmen (unter Anderem: keine Impulsinterferenzen) getroffen. Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im

Kapitel 15: Codierte und mehrstufige Übertragung, Programm "cod"

des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf

dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
dieser Praktikumsanleitung ⇒ Link verweist auf die PDF-Version; Kapitel 15: Seite 337-362.

Informationsgehalt – Entropie – Redundanz

Wir gehen von einer $M$ –stufigen digitalen Nachrichtenquelle aus, die folgendes Quellensignal abgibt:

$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)\hspace{0.3cm}{\rm mit}\hspace{0.3cm}a_\nu \in \{ a_1, \text{...} \ , a_\mu , \text{...} \ , a_{ M}\}.$

Die Quellensymbolfolge $\langle q_\nu \rangle$ ist also auf die Folge $\langle a_\nu \rangle$ der dimensionslosen Amplitudenkoeffizienten abgebildet.
Vereinfachend wird zunächst für die zeitliche Laufvariable $\nu = 1$ , ... , $N$ gesetzt, während der Vorratsindex $\mu$ stets Werte zwischen $1$ und $M$ annehmen kann.

Ist das $\nu$ –te Folgenelement gleich $a_\mu$ , so kann dessen Informationsgehalt mit der Wahrscheinlichkeit $p_{\nu\mu} = {\rm Pr}(a_\nu = a_\mu)$ wie folgt berechnet werden:

$I_\nu = \log_2 \ (1/p_{\nu \mu})= {\rm ld} \ (1/p_{\nu \mu}) \hspace{1cm}\text{(Einheit: bit)}\hspace{0.05cm}.$

Der Logarithmus zur Basis 2 ⇒ $\log_2(x)$ wird oft auch mit ${\rm ld}(x)$ ⇒ "Logarithmus dualis" bezeichnet. Bei der numerischen Auswertung wird die Hinweiseinheit „bit” (von: "binary digit" ) hinzugefügt. Mit dem Zehner–Logarithmus $\lg(x)$ bzw. dem natürlichen Logarithmus $\ln(x)$ gilt:

${\rm log_2}(x) = \frac{{\rm lg}(x)}{{\rm lg}(2)}= \frac{{\rm ln}(x)}{{\rm ln}(2)}\hspace{0.05cm}.$

Nach dieser auf Claude E. Shannon zurückgehenden Definition von Information ist der Informationsgehalt eines Symbols umso größer, je kleiner dessen Auftrittswahrscheinlichkeit ist.

$\text{Definition:}$ Die Entropie ist der mittlere Informationsgehalt eines Folgenelements (Symbols). Diese wichtige informationstheoretische Größe lässt sich als Zeitmittelwert wie folgt ermitteln:

$H = \lim_{N \to \infty} \frac{1}{N} \cdot \sum_{\nu = 1}^N I_\nu = \lim_{N \to \infty} \frac{1}{N} \cdot \sum_{\nu = 1}^N \hspace{0.1cm}{\rm log_2}\hspace{0.05cm} \ (1/p_{\nu \mu}) \hspace{1cm}\text{(Einheit: bit)}\hspace{0.05cm}.$

Natürlich kann die Entropie auch durch Scharmittelung (über den Symbolvorrat) berechnet werden.

Hinweise:

Sind die Folgenelemente $a_\nu$ statistisch voneinander unabhängig, so sind die Auftrittswahrscheinlichkeiten $p_{\nu\mu} = p_{\mu}$ unabhängig von $\nu$ und man erhält in diesem Sonderfall für die Entropie:

$H = \sum_{\mu = 1}^M p_{ \mu} \cdot {\rm log_2}\hspace{0.1cm} \ (1/p_{\mu})\hspace{0.05cm}.$

Bestehen dagegen statistische Bindungen zwischen benachbarten Amplitudenkoeffizienten $a_\nu$ , so muss zur Entropieberechnung die kompliziertere Gleichung entsprechend obiger Definition herangezogen werden.

$\text{Definitionen:}$

Der Maximalwert der Entropie ⇒ Entscheidungsgehalt ergibt sich immer dann, wenn die $M$ Auftrittswahrscheinlichkeiten (der statistisch unabhängigen Symbole) alle gleich sind $(p_{\mu} = 1/M)$ :

$H_{\rm max} = \sum_{\mu = 1}^M \hspace{0.1cm}\frac{1}{M} \cdot {\rm log_2} (M) = {\rm log_2} (M) \cdot \sum_{\mu = 1}^M \hspace{0.1cm} \frac{1}{M} = {\rm log_2} (M) \hspace{1cm}\text{(Einheit: bit)}\hspace{0.05cm}.$

Die relative Redundanz ist dann der folgende Quotient:

$r = \frac{H_{\rm max}-H}{H_{\rm max} }.$

Da stets $0 \le H \le H_{\rm max}$ gilt, kann die relative Redundanz Werte zwischen $0$ und $1$ (einschließlich dieser Grenzwerte) annehmen.

Aus der Herleitung dieser Beschreibungsgrößen ist offensichtlich, dass ein redundanzfreies Digitalsignal $(r=0)$ folgende Eigenschaften erfüllen muss:

Die Amplitudenkoeffizienten $a_\nu$ sind statistisch unabhängig ⇒ $p_{\nu\mu} = {\rm Pr}(a_\nu = a_\mu)$ ist für alle $\nu$ identisch.
Die $M$ möglichen Koeffizienten $a_\mu$ treten mit gleicher Wahrscheinlichkeit $p_\mu = 1/M$ auf.

$\text{Beispiel 1:}$ Analysiert man einen zur Übertragung anstehenden deutschen Text auf der Basis von $M = 32$ Zeichen:

$\text{ a, ... , z, ä, ö, ü, ß, Leerzeichen, Interpunktion, keine Unterscheidung zwischen Groß– und Kleinschreibung },$

so ergibt sich der Entscheidungsgehalt $H_{\rm max} = 5 \ \rm bit/Symbol$ . Aufgrund

der unterschiedlichen Häufigkeiten $($ beispielsweise tritt „e” deutlich häufiger auf als „u” $)$ und
von statistischen Bindungen $($ zum Beispiel folgt auf „q” der Buchstabe „u” viel öfters als „e” $)$

beträgt nach Karl Küpfmüller die Entropie der deutschen Sprache nur $H = 1.3 \ \rm bit/Zeichen$ . Daraus ergibt sich die relative Redundanz zu $r \approx (5 - 1.3)/5 = 74\%$ .

Für englische Texte hat Claude Shannon die Entropie mit $H = 1 \ \rm bit/Zeichen$ und die relative Redundanz mit $r \approx 80\%$ angegeben.

Quellencodierung – Kanalcodierung – Übertragungscodierung

Unter "Codierung" versteht man die Umsetzung der Quellensymbolfolge $\langle q_\nu \rangle$ mit dem Symbolumfang $M_q$ in eine Codesymbolfolge $\langle c_\nu \rangle$ mit dem Symbolumfang $M_c$ . Meist wird durch die Codierung die in einem Digitalsignal enthaltene Redundanz manipuliert. Oft – aber nicht immer – sind $M_q$ und $M_c$ verschieden.

Man unterscheidet je nach Zielrichtung zwischen verschiedenen Arten von Codierung:

Die Aufgabe der Quellencodierung ist die Redundanzreduktion zur Datenkomprimierung, wie sie beispielsweise in der Bildcodierung Anwendung findet. Durch Ausnutzung statistischer Bindungen zwischen den einzelnen Punkten eines Bildes bzw. zwischen den Helligkeitswerten eines Punktes zu verschiedenen Zeiten (bei Bewegtbildsequenzen) können Verfahren entwickelt werden, die bei nahezu gleicher (subjektiver) Bildqualität zu einer merklichen Verminderung der Datenmenge (gemessen in „bit” oder „byte”) führen. Ein einfaches Beispiel hierfür ist die "differentielle Pulscodemodulation $\rm (DPCM)$ .

Bei der Kanalcodierung erzielt man demgegenüber dadurch eine merkliche Verbesserung des Übertragungsverhaltens, dass eine beim Sender gezielt hinzugefügte Redundanz empfangsseitig zur Erkennung und Korrektur von Übertragungsfehlern genutzt wird. Solche Codes, deren wichtigste Vertreter Blockcodes, Faltungscodes und Turbo-Codes sind, haben besonders bei stark gestörten Kanälen eine große Bedeutung. Je größer die relative Redundanz des codierten Signals ist, desto besser sind die Korrektureigenschaften des Codes, allerdings bei verringerter Nutzdatenrate.

Eine Übertragungscodierung – häufig auch als "Leitungscodierung" bezeichnet – verwendet man, um das Sendesignal durch eine Umcodierung der Quellensymbole an die Spektraleigenschaften von Übertragungskanal und Empfangseinrichtungen anzupassen. Beispielsweise muss bei einem Kanal mit der Frequenzgangseigenschaft $H_{\rm K}(f=0) = 0$ , über den demzufolge kein Gleichsignal übertragen werden kann, durch Übertragungscodierung sichergestellt werden, dass die Codesymbolfolge weder eine lange $\rm L$ – noch eine lange $\rm H$ –Folge beinhaltet.

Im vorliegenden Buch „Digitalsignalübertragung” beschäftigen wir uns ausschließlich mit diesem letzten, übertragungstechnischen Aspekt.

Der Kanalcodierung ist in unserem Lerntutorial ein eigenes Buch gewidmet.
Die Quellencodierung wird im Buch Informationstheorie (Hauptkapitel 2) ausführlich behandelt.
Auch die im Buch „Beispiele von Nachrichtensystemen” beschriebene Sprachcodierung ist eine spezielle Form der Quellencodierung.

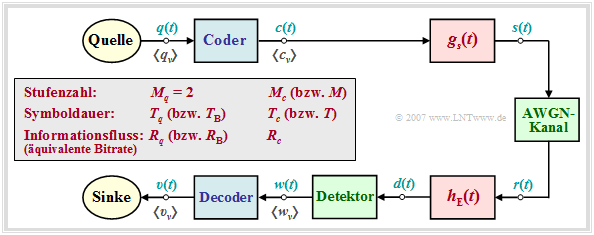
Systemmodell und Beschreibungsgrößen

Im Folgenden gehen wir stets von dem unten skizzierten Blockschaltbild und folgenden Vereinbarungen aus:

Blockschaltbild zur Beschreibung mehrstufiger und codierter Übertragungssysteme

Das digitale Quellensignal $q(t)$ sei binär $(M_q = 2)$ und redundanzfrei $(H_q = 1 \ \rm bit/Symbol)$ .

Mit der Symboldauer $T_q$ ergibt sich für die Symbolrate der Quelle:

$R_q = {H_{q}}/{T_q}= {1}/{T_q}\hspace{0.05cm}.$

Wegen $M_q = 2$ bezeichnen wir im Folgenden $T_q$ auch als die "Bitdauer" und $R_q$ als die "Bitrate".

Für den Vergleich von Übertragungssystemen mit unterschiedlicher Codierung werden $T_q$ und $R_q$ stets als konstant angenommen. Hinweis: In späteren Kapiteln verwenden wir hierfür $T_{\rm B}$ und $R_{\rm B}$ .

Das Codersignal $c(t)$ und nach der Impulsformung mit $g_s(t)$ auch das Sendesignal $s(t)$ besitzen die Stufenzahl $M_c$ , die Symboldauer $T_c$ und die Symbolrate $1/T_c$ . Die äquivalente Bitrate beträgt

$R_c = {{\rm log_2} (M_c)}/{T_c} \ge R_q\hspace{0.05cm}.$

Das Gleichheitszeichen gilt nur bei den redundanzfreien Codes $(r_c = 0)$ .
Andernfalls erhält man für die relative Coderedundanz:

$r_c =({R_c - R_q})/{R_c} = 1 - R_q/{R_c} \hspace{0.05cm}.$

Hinweise zur Nomenklatur:

Im Zusammenhang mit Übertragungscodes gibt $R_c$ in unserem Lerntutorial stets die äquivalente Bitrate des Codersignals an.
Diese hat ebenso wie die Quellenbitrate $R_q$ die Einheit „bit/s”.
Insbesondere in der Literatur zur Kanalcodierung bezeichnet man dagegen mit $R_c$ oft die dimensionslose Coderate $1 - r_c$ .
$R_c = 1$ gibt dann einen redundanzfreien Code an, während $R_c = 1/3$ einen Code mit der relativen Redundanz $r_c = 2/3$ kennzeichnet.

$\text{Beispiel 2:}$ Bei den so genannten "4B3T–Codes" werden

jeweils vier Binärsymbole $(m_q = 4, \ M_q= 2)$
durch drei Ternärsymbole $(m_c = 3, \ M_c= 3)$

dargestellt. Wegen $4 \cdot T_q = 3 \cdot T_c$ gilt:

$R_q = {1}/{T_q}, \hspace{0.1cm} R_c = { {\rm log_2} (3)} \hspace{-0.05cm} /{T_c} = {3/4 \cdot {\rm log_2} (3)} \hspace{-0.05cm}/{T_q}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}r_c =3/4\cdot {\rm log_2} (3) \hspace{-0.05cm}- \hspace{-0.05cm}1 \approx 15.9\, \% \hspace{0.05cm}.$

Genauere Informationen zu den 4B3T-Codes finden Sie im gleichnamigen Kapitel .

AKF–Berechnung eines Digitalsignals

Zur Vereinfachung der Schreibweise wird im Folgenden $M_c = M$ und $T_c = T$ gesetzt. Damit kann für das Sendesignal $s(t)$ bei einer zeitlich unbegrenzten Nachrichtenfolge mit $a_\nu \in \{ a_1,$ ... , $a_M\}$ geschrieben werden:

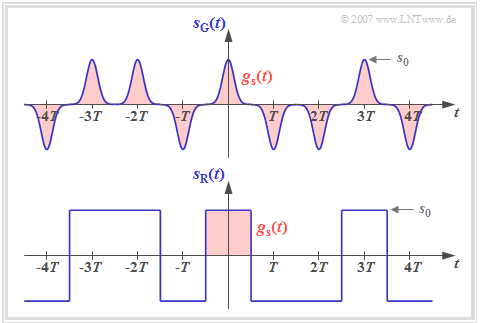
Zwei verschiedene binäre bipolare Sendesignale

$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T) \hspace{0.05cm}.$

Diese Signaldarstellung beinhaltet sowohl die Quellenstatistik $($ Amplitudenkoeffizienten $a_\nu$ ) als auch die Sendeimpulsform $g_s(t)$ . Die Grafik zeigt zwei binäre bipolare Sendesignale $s_{\rm G}(t)$ und $s_{\rm R}(t)$ mit gleichen Amplitudenkoeffizienten $a_\nu$ , die sich somit lediglich durch den Sendegrundimpuls $g_s(t)$ unterscheiden.

Man erkennt aus dieser Darstellung, dass ein Digitalsignal im Allgemeinen nichtstationär ist:

Beim Sendesignal $s_{\rm G}(t)$ mit schmalen Gaußimpulsen ist die Nichtstationarität offensichtlich, da zum Beispiel bei Vielfachen von $T$ die Varianz $\sigma_s^2 = s_0^2$ ist, während genau dazwischen $\sigma_s^2 \approx 0$ gilt.

Auch das Signal $s_{\rm R}(t)$ mit NRZ–rechteckförmigen Impulsen ist im strengen Sinne nichtstationär, da sich hier die Momente an den Bitgrenzen gegenüber allen anderen Zeitpunkten unterscheiden. Im gezeichneten Beispiel gilt $s_{\rm R}(t = \pm T/2)=0$ .

$\text{Definition:}$ Einen Zufallsprozess, dessen Momente $m_k(t) = m_k(t+ \nu \cdot T)$ sich periodisch mit $T$ wiederholen, bezeichnet man als zyklostationär;
$k$ und $\nu$ besitzen bei dieser impliziten Definition ganzzahlige Zahlenwerte.

Viele der Regeln für ergodische Prozesse kann man mit nur geringen Einschränkungen auch auf "zykloergodische" (und damit "zyklostationäre") Prozesse anwenden.

Insbesondere gilt für die Autokorrelationsfunktion $\rm (AKF)$ solcher Zufallsprozesse mit Mustersignal $s(t)$ :

$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] \hspace{0.05cm}.$

Mit obiger Gleichung des Sendesignals kann die AKF als Zeitmittelwert auch wie folgt geschrieben werden:

$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}\frac{1}{T} \cdot \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = -N}^{+N} a_\nu \cdot a_{\nu + \lambda} \cdot \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau - \lambda \cdot T)\,{\rm d} t \hspace{0.05cm}.$

Da die Grenzwert–, Integral– und Summenbildung miteinander vertauscht werden darf, kann mit den Substitutionen

$N = T_{\rm M}/(2T), \hspace{0.5cm}\lambda = \kappa- \nu,\hspace{0.5cm}t - \nu \cdot T \to T$

hierfür auch geschrieben werden:

$\varphi_s(\tau) = \lim_{T_{\rm M} \to \infty}\frac{1}{T_{\rm M}} \cdot \int_{-T_{\rm M}/2}^{+T_{\rm M}/2} \sum_{\nu = -\infty}^{+\infty} \sum_{\kappa = -\infty}^{+\infty} a_\nu \cdot g_s ( t - \nu \cdot T ) \cdot a_\kappa \cdot g_s ( t + \tau - \kappa \cdot T ) \,{\rm d} t \hspace{0.05cm}.$

Nun werden zur Abkürzung folgende Größen eingeführt:

$\text{Definition:}$

Die diskrete AKF der Amplitudenkoeffizienten liefert Aussagen über die linearen statistischen Bindungen der Amplitudenkoeffizienten $a_{\nu}$ und $a_{\nu + \lambda}$ und besitzt keine Einheit:

$\varphi_a(\lambda) = \lim_{N \to \infty} \frac{1}{2N +1} \cdot \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot a_{\nu + \lambda} \hspace{0.05cm}.$

Die Energie–AKF des Grundimpulses ist ähnlich definiert wie die allgemeine (Leistungs–) AKF. Sie wird mit einem Punkt gekennzeichnet:

$\varphi^{^{\bullet} }_{gs}(\tau) = \int_{-\infty}^{+\infty} g_s ( t ) \cdot g_s ( t + \tau)\,{\rm d} t \hspace{0.05cm}.$

⇒ Da

$g_s(t)$ energiebegrenzt ist, kann auf die Division durch

$T_{\rm M}$ und den Grenzübergang verzichtet werden.

Für die Autokorrelationsfunktion eines Digitalsignals $s(t)$ gilt allgemein:

$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$

⇒

$s(t)$ kann dabei binär oder mehrstufig, unipolar oder bipolar sowie redundanzfrei oder redundant (leitungscodiert) sein.

⇒ Die Impulsform wird durch die Energie–AKF berücksichtigt.

Anmerkungen:

Beschreibt das Digitalsignal $s(t)$ einen Spannungsverlauf,

so hat die Energie–AKF des Grundimpulses $g_s(t)$ die Einheit $\rm V^2s$
und die Autokorrelationsfunktion $\varphi_s(\tau)$ des Digitalsignals $s(t)$ die Einheit $\rm V^2$ , jeweils bezogen auf den Widerstand $1 \ \rm \Omega$ .

Im strengen Sinne der Systemtheorie müsste man die AKF der Amplitudenkoeffizienten wie folgt definieren:

$\varphi_{a , \hspace{0.08cm}\delta}(\tau) = \sum_{\lambda = -\infty}^{+\infty} \varphi_a(\lambda)\cdot \delta(\tau - \lambda \cdot T)\hspace{0.05cm}.$

⇒ Damit würde sich die obige Gleichung wie folgt darstellen:

$\varphi_s(\tau) ={1}/{T} \cdot \varphi_{a , \hspace{0.08cm} \delta}(\tau)\star \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$

⇒ Zur einfacheren Darstellung wird im Folgenden die diskrete AKF der Amplitudenkoeffizienten ⇒

$\varphi_a(\lambda)$ ohne diese Diracfunktionen geschrieben.

LDS–Berechnung eines Digitalsignals

Die Entsprechungsgröße zur Autokorrelationsfunktion $\rm (AKF)$ eines Zufallssignals ⇒ $\varphi_s(\tau)$ ist im Frequenzbereich das Leistungsdichtespektrum $\rm (LDS)$ ⇒ ${\it \Phi}_s(f)$ , das mit der AKF über das Fourierintegral in einem festen Bezug steht:

$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} \,{\rm d} \tau \hspace{0.05cm}.$

Berücksichtigt man den Zusammenhang zwischen Energie–AKF und Energiespektrum,

$\varphi^{^{\hspace{0.05cm}\bullet}}_{gs}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{gs}(f) = |G_s(f)|^2 \hspace{0.05cm},$

sowie den Verschiebungssatz, so kann das Leistungsdichtespektrum des Digitalsignals

$s(t)$ in folgender Weise dargestellt werden:

${\it \Phi}_s(f) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot {\it \Phi}^{^{\hspace{0.05cm}\bullet}}_{gs}(f) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = {1}/{T} \cdot |G_s(f)|^2 \cdot \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot \cos ( 2 \pi f \lambda T)\hspace{0.05cm}.$

Hierbei ist berücksichtigt, dass

${\it \Phi}_s(f)$ und

$|G_s(f)|^2$ reellwertig sind und gleichzeitig

$\varphi_a(-\lambda) =\varphi_a(+\lambda)$ gilt.

Definiert man nun die spektrale Leistungsdichte der Amplitudenkoeffizienten zu

${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda \hspace{0.02cm}T} = \varphi_a(0) + 2 \cdot \sum_{\lambda = 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f \lambda T) \hspace{0.05cm},$

so erhält man den folgenden Ausdruck:

${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot |G_s(f)|^2 \hspace{0.05cm}.$

$\text{Fazit:}$ Das Leistungsdichtespektrum ${\it \Phi}_s(f)$ eines Digitalsignals $s(t)$ kann als Produkt zweier Funktionen dargestellt werden:

Der erste Term ${\it \Phi}_a(f)$ ist dimensionslos und beschreibt die spektrale Formung des Sendesignals durch die statistischen Bindungen der Quelle.
Dagegen berücksichtigt $\vert G_s(f) \vert^2$ die spektrale Formung durch den Sendegrundimpuls $g_s(t)$ .
Je schmaler dieser ist, desto breiter ist $\vert G_s(f) \vert^2$ und um so größer ist damit der Bandbreitenbedarf.
Das Energiespektrum hat die Einheit $\rm V^2s/Hz$ und das Leistungsdichtespektrum – aufgrund der Division durch den Symbolabstand $T$ – die Einheit $\rm V^2/Hz$ .
Beide Angaben gelten wieder nur für den Widerstand $1 \ \rm \Omega$ .

AKF und LDS bei bipolaren Binärsignalen

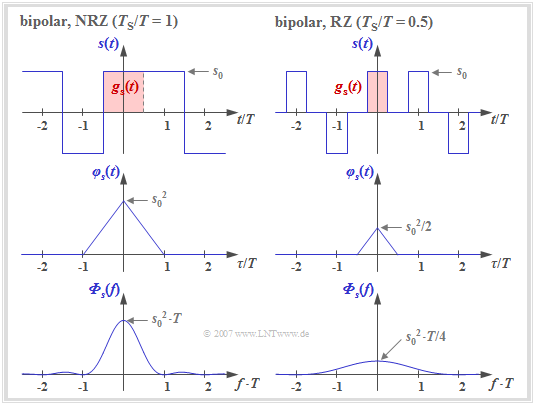
Die bisherigen Ergebnisse werden nun an Beispielen verdeutlicht. Ausgehend von binären bipolaren Amplitudenkoeffizienten $a_\nu \in \{-1, +1\}$ erhält man, falls keine Bindungen zwischen den einzelnen Amplitudenkoeffizienten $a_\nu$ bestehen:

Signalausschnitt, AKF und LDS bei binärer bipolarer Signalisierung

$\varphi_a(\lambda) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \lambda \ne 0 \\ \end{array} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\varphi_s(\tau)= {1}/{T} \cdot \varphi^{^{\bullet}}_{gs}(\tau)\hspace{0.05cm}.$

Die Grafik zeigt zwei Signalausschnitte jeweils mit Rechteckimpulsen $g_s(t)$ , die dementsprechend zu einer dreieckförmigen Autokorrelationsfunktion $\rm (AKF)$ und zu einem $\rm si^2$ –förmigen Leistungsdichtespektrum $\rm (LDS)$ führen.

Die linken Bilder beschreiben eine NRZ–Signalisierung. Das heißt: Die Breite $T_{\rm S}$ des Grundimpulses ist gleich dem Abstand $T$ zweier Sendeimpulse (Quellensymbole).

Dagegen gelten die rechten Bilder für einen RZ–Impuls mit dem Tastverhältnis $T_{\rm S}/T = 0.5$ .

Man erkennt aus diesen Darstellungen:

Bei NRZ–Rechteckimpulsen ergibt sich für die (auf den Widerstand $1 \ \rm \Omega$ bezogene) Sendeleistung $P_{\rm S} = \varphi_s(\tau = 0) = s_0^2$ .
Die dreieckförmige AKF ist auf den Bereich $|\tau| \le T_{\rm S}= T$ beschränkt.
Das LDS ${\it \Phi}_s(f)$ als die Fouriertransformierte von $\varphi_s(\tau)$ ist $\rm si^2$ –förmig mit äquidistanten Nullstellen im Abstand $1/T$ .
Die Fläche unter der LDS–Kurve ergibt wieder die Sendeleistung $P_{\rm S} = s_0^2$ .

Im Fall der RZ–Signalisierung (rechte Rubrik) ist die dreieckförmige AKF gegenüber dem linken Bild in Höhe und Breite jeweils um den Faktor $T_{\rm S}/T = 0.5$ kleiner.

$\text{Fazit:}$ Vergleicht man die beiden Leistungsdichtespektren $($ untere Bilder $)$ , so erkennt man für $T_{\rm S}/T = 0.5$ $($ RZ–Impuls $)$ gegenüber $T_{\rm S}/T = 1$ $($ NRZ–Impuls $)$

eine Verkleinerung in der Höhe um den Faktor $4$
und eine Verbreiterung um den Faktor $2$ .

Die Fläche $($ Leistung $)$ ist somit halb so groß, da in der Hälfte der Zeit $s(t) = 0$ gilt.

AKF und LDS bei unipolaren Binärsignalen

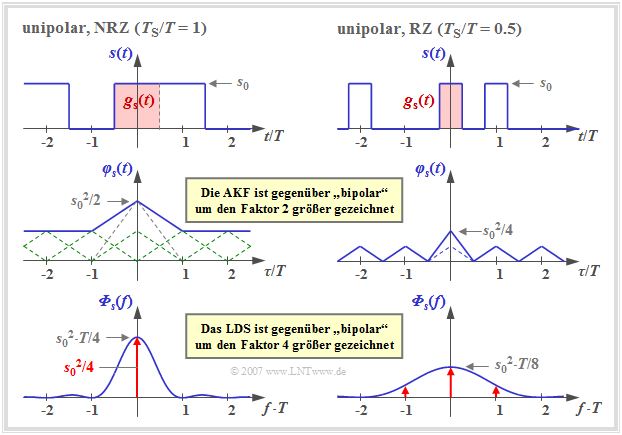
Wir gehen weiterhin von NRZ– bzw. RZ–Rechteckimpulsen aus. Die binären Amplitudenkoeffizienten seien aber nun unipolar: $a_\nu \in \{0, 1\}$ . Dann gilt für die diskrete AKF der Amplitudenkoeffizienten:

Signalausschnitt, AKF und LDS bei binärer unipolarer Signalisierung

$\varphi_a(\lambda) = \left\{ \begin{array}{c} m_2 = 0.5 \\ \\ m_1^2 = 0.25 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\lambda = 0, \\ \\ \lambda \ne 0 \hspace{0.05cm}.\\ \end{array}$

Vorausgesetzt sind gleichwahrscheinliche Amplitudenkoeffizienten ⇒ ${\rm Pr}(a_\nu =0) = {\rm Pr}(a_\nu =1) = 0.5$ ohne statistische Bindungen, so dass sowohl das zweite Moment $m_2$ (Leistung) als auch der lineare Mittelwert $m_1$ (Gleichanteil) jeweils $0.5$ sind.

Die Grafik zeigt einen Signalausschnitt, die AKF und das LDS mit unipolaren Amplitudenkoeffizienten,

links für rechteckförmige NRZ–Impulse $(T_{\rm S}/T = 1)$ , und
rechts für RZ–Impulse mit dem Tastverhältnis $T_{\rm S}/T = 0.5$ .

Es gibt folgende Unterschiede gegenüber bipolarer Signalisierung:

Durch die Addition der unendlich vielen Dreieckfunktionen im Abstand $T$ , alle mit gleicher Höhe, ergibt sich für die AKF in der linken Grafik (NRZ) ein konstanter Gleichanteil $s_0^2/4$ .

Daneben verbleibt im Bereich $|\tau| \le T_{\rm S}$ ein einzelnes Dreieck ebenfalls mit Höhe $s_0^2/4$ , das im Leistungsdichtespektrum (LDS) zum $\rm si^2$ –förmigen Verlauf führt (blaue Kurve).

Der Gleichanteil in der AKF hat im LDS eine Diracfunktion bei der Frequenz $f = 0$ mit dem Gewicht $s_0^2/4$ zur Folge. Dadurch wird der LDS–Wert ${\it \Phi}_s(f=0)$ unendlich groß.

Aus der rechten Grafik – gültig für $T_{\rm S}/T = 0.5$ – erkennt man, dass sich nun die AKF aus einem periodischen Dreiecksverlauf (im mittleren Bereich gestrichelt eingezeichnet) und zusätzlich noch aus einem einmaligen Dreieck im Bereich $|\tau| \le T_{\rm S} = T/2$ mit Höhe $s_0^2/8$ zusammensetzt.

Diese einmalige Dreieckfunktion führt zum kontinuierlichen $\rm si^2$ –förmigen Anteil (blaue Kurve) von ${\it \Phi}_s(f)$ mit der ersten Nullstelle bei $1/T_{\rm S} = 2/T$ .

Dagegen führt die periodische Dreieckfunktion nach den Gesetzmäßigkeiten der Fourierreihe zu einer unendlichen Summe von Diracfunktionen mit unterschiedlichen Gewichten im Abstand $1/T$ (rot gezeichnet).

Die Gewichte der Diracfunktionen sind proportional zum kontinuierlichen (blauen) LDS–Anteil. Das maximale Gewicht $s_0^2/8$ besitzt die Diraclinie bei $f = 0$ . Dagegen sind die Diraclinien bei $\pm 2/T$ und Vielfachen davon nicht vorhanden bzw. besitzen jeweils das Gewicht $0$ , da hier auch der kontinuierliche LDS–Anteil Nullstellen hat.

$\text{Hinweis:}$

Unipolare Amplitudenkoeffizienten treten zum Beispiel bei optischen Übertragungssystemen auf.
In späteren Kapiteln beschränken wir uns aber meist auf die bipolare Signalisierung.

Aufgaben zum Kapitel

Aufgabe 2.1: AKF und LDS nach Codierung

Aufgabe 2.1Z: Zur äquivalenten Bitrate

Aufgabe: 2.2 Binäre bipolare Rechtecke