Aufgabe 4.5Z: Nochmals Impulsantwort
Wir betrachten wieder wie in der Aufgabe 4.5 ein binäres Übertragungssystem mit der Bitrate $R$ und der Symboldauer $T= 1/R$. Als Übertragungsmedium wird ein Normalkoaxialkabel (Innendurchmesser: 2.6 mm, Außendurchmesser: 9.5 mm) der Länge $l = 1 \ \rm km$ mit folgendem Frequenzgang verwendet: $$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1 \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot {\rm e}^{- \alpha_2 \hspace{0.01cm} \sqrt{f} \hspace{0.05cm}l} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2 \hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} = H_1(f) \cdot H_2(f) \cdot H_3(f)$$
Die Teilfrequenzgänge $H_1(f)$, $H_2(f)$ und $H_3(f)$ dienen hier nur als Abkürzung. Die Leitungsparameter lauten:
$$\beta_1 = 21.78\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm}, \hspace{0.2cm}
\alpha_2 = 0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}}\hspace{0.05cm},\hspace{0.2cm}
\beta_2 = 0.2722\, \frac{\rm rad}{\rm km \cdot \sqrt{MHz}}
\hspace{0.05cm}.$$
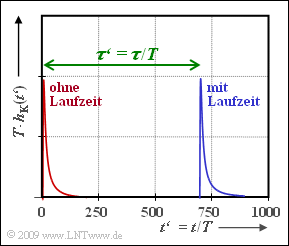
Die Grafik zeigt die resultierende Impulsantwort $h_{\rm K}(t')$, wobei $t' = t/T$ die normierte Zeit darstellt. Ohne Berücksichtigung der (normierten) Phasenlaufzeit$\tau' = \tau/T$ kann $h_{\rm K}(t')$ wie folgt geschrieben werden:
$$h_{\rm K}(t') = \frac {1}{T} \cdot \frac {\rm a_\rm \star/\pi}{ \sqrt{2
\hspace{0.05cm}t'^3}}\cdot {\rm exp} \left [ -\frac {\rm a_\rm \star^2}{ {2\pi
\hspace{0.05cm}t'}} \right ] \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm}
{\rm mit}\hspace{0.15cm}{\rm a}_{\rm \star}\hspace{0.15cm}
{\rm in}\hspace{0.15cm}
{\rm Neper}\hspace{0.05cm}.$$
Diese Gleichung gibt die Fourierrücktransformierte des Produkts $H_2(f) \cdot H_3(f)$ an. Verwendet ist dabei die charakteristische Kabeldämpfung ${\rm a}_{\rm \star} = \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$
Hinweise:
- Die Aufgabe gehört zum Kapitel Eigenschaften von Koaxialkabeln.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
- Sie können zur Überprüfung Ihrer Ergebnisse das Interaktionsmodul Zeitverhalten von Kupferkabeln benutzen.
- In der Aufgabe 4.5 wurde der Maximalwert der normierten Impulsantwort wie folgt berechnet:
$${\rm Max}[T \cdot h_{\rm K}(t)] = \frac {\sqrt{13.5 \pi} \cdot {\rm e}^{-1.5} }{{\rm a}_{\rm \star}^2} \approx \frac {1.453 }{{\rm a}_{\rm \star}^2} \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm mit}\hspace{0.15cm}{\rm a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$
Fragebogen
Musterlösung
- 1. Die Spektraldarstellung eines Laufzeitgliedes lautet e–j2πfτ. Ein Vergleich mit der Angabenseite zeigt, dass H1(f) genau diesem Ansatz genügt ⇒ Alternative 1.
- 2. Entsprechend dem Angabenblatt gilt:
- $$2\pi \cdot f \cdot \tau = \beta_1 \cdot f \cdot l \Rightarrow \hspace{0.3cm}\tau= \frac {\beta_1 \cdot l}{2\pi} = \frac {21.78\, {\rm rad}/{({\rm km \cdot MHz})}\cdot 10\,{\rm km}}{2\pi} = 34.7\,{\rm \mu s}$$
- $$\Rightarrow \hspace{0.3cm}\tau '= {\tau}/{T} = 694 \Rightarrow \hspace{0.3cm} T = \frac {34.7\,{\rm \mu s}}{700} \approx 0.05\,{\rm \mu s}\hspace{0.05cm}.$$
- Die Bitrate ist gleich dem Kehrwert der Symboldauer: R = 20 Mbit/s.
- 3. Für die charakteristische Kabeldämpfung erhält man somit:
- $${\rm a}_{\rm \star} = \alpha_2 \cdot \sqrt {R/2} \cdot l = 0.2722\, \frac{\rm Np}{\rm km \cdot \sqrt{MHz}} \cdot \sqrt {10\,{\rm MHz}} \cdot 10\,{\rm km} \hspace{0.15cm}\underline{\approx 8.6\,{\rm Np}}\hspace{0.05cm}.$$
- Der entsprechende dB–Wert ist 75 dB.
- 4. Mit der angegebenen Gleichung und dem Ergebnis aus c) ergibt sich:
- $${\rm Max}[T \cdot h_{\rm K}(t)] \approx \frac {1.453 }{{\rm a}_{\rm \star}^2} = \frac {1.453 }{8.6^2} \hspace{0.15cm}\underline{ \approx 0.02}\hspace{0.05cm}.$$
- 5. Richtig ist nur Aussage 1. H1(f) beschreibt die frequenzunabhängige Laufzeit, die keine Verzerrung zur Folge hat. Dagegen sollte man zur Berechnung der Impulsantwort auf keinen Fall auf H2(f) oder H3(f) verzichten, da es sonst es zu gravierenden Fehlern kommen würde:
- Die Impulsantwort h2(t) als die Fourierrücktransformierte von H2(f) ist eine gerade Funktion mit dem Maximum bei t = 0 und erstreckt sich in beide Richtungen über Hunderte von Symbolen.
- Dagegen ist die Fourierrücktransformierte von H3(f) eine ungerade Funktion mit einer Sprungstelle bei t = 0. Für t > 0 fällt h3(t) ähnlich – aber nicht exakt – wie eine Exponentialfunktion ab. Für negative Zeiten gilt h3(t) = – h3(|t|).
- Erst die Faltung h2(t) ∗ h3(t) liefert die kausale Impulsantwort. Die Phasenlaufzeit τ ist hierbei noch nicht berücksichtigt.