Aufgabe 1.3: ISDN–Rahmenstruktur

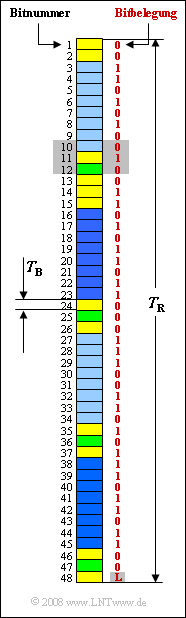
Rahmenstruktur der $\rm S_{0}$–Schnittstelle

Die Grafik zeigt die Rahmenstruktur der $\rm S_{0}$–Schnittstelle. Jeder Rahmen der Dauer $T_{\rm R}$ beinhaltet $48$ Bit, darunter:

$16$ Bit für den Bearer Channel $\rm B1$ (hellblau),
$16$ Bit für den Bearer Channel $\rm B2$ (dunkelblau),
$4$ Bit für den Data Channel $\rm D$ (grün).

Gelb eingezeichnet sind die erforderlichen Steuerbits.

Vorgegeben wird für diese Aufgabe, dass jeder der beiden Basiskanäle $\rm B1$ und $\rm B2$ eine Nettodatenrate von $R_{\rm B} = 64 \ \rm kbit/s$ bereitstellen soll.

Anzumerken ist noch, dass die Bitdauer $T_{\rm B}$ des uncodierten Binärsignals gleichzeitig die Symboldauer des (modifizierten) AMI–Codes angibt, der jede binäre „$1$” dem Spannungspegel $0 \ \rm V$ zuordnet und jede binäre „$0$” alternierend mit $+0.75 \ \rm V$ bzw. $–0.75 \ \rm V$ darstellt.

Die Zahlenwerte in der Grafik (rot markiert) geben eine Beispielfolge an, die in der Teilaufgabe (5) entsprechend dem modifizierten AMI–Code in Spannungspegel umgesetzt werden soll.

Bitnummer $48$ beinhaltet das so genannte L–Bit.
Dieses ist in der Teilaufgabe (6) so zu setzen, dass das Signal $s(t)$ gleichsignalfrei wird.

Hinweise:

Die Aufgabe gehört zum Kapitel ISDN-Basisanschluss.
Der (modifizierte) AMI–Code wird ausführlich in Eigenschaften des AMI-Codes im Buch „Digitalsignalübertragung” beschrieben.
Anzumerken ist ferner, dass die ersten $47$ Bit genau $22$ „Nullen” enthalten.

Fragebogen

$T_{\rm R} \ = \ $

$\ \rm \mu s$

$T_{\rm B} \ = \ $

$\ \rm \mu s $

$R_{\rm ges} \ = \ $

$\ \rm kbit/s$

$N_{\rm St} \ = \ $

$U_{10} \ = \ $

$\ \rm V $

$U_{11} \ = \ $

$\ \rm V $

$U_{12} \ = \ $

$\ \rm V $

$U_{48} \ = \ $

$\ \rm V $

Musterlösung

(1) In jedem Rahmen werden jeweils 16 Bit der Basiskanäle B1 und B2 übertragen. Mit der Rahmendauer $T_{\rm R}$ gilt somit für die Bitrate $(R_{\rm B} = 64 \ \rm kbit/s)$ eines jeden Rahmens:

$$R_{\rm B} = \frac{16\,\,{\rm bit}}{T_{\rm R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm R} = \frac{16\,\,{\rm bit}}{64 \cdot 10^3\,\,{\rm bit/s}} \hspace{0.15cm}\underline{= 250 \,{\rm \mu s}} \hspace{0.05cm}.$$

(2) Für jedes einzelne der 48 Bit steht somit die Zeitdauer

$$T_{\rm B} = \frac{T_{\rm R}}{48} = \frac{250 \,{\rm \mu s}}{48} \hspace{0.15cm}\underline{ = 5.208 \,{\rm \mu s}}$$

zur Verfügung. Da bei der (modifizierten) AMI–Codierung jedes Binärsymbol durch ein Ternärsymbol gleicher Dauer ersetzt wird, ist die Symboldauer nach der AMI–Codierung ebenfalls gleich $T_{\rm B}$.

(3) Die Bruttodatenrate ist gleich dem Kehrwert der Bitdauer:

$$R_{\rm ges} = \frac{1}{T_{\rm B}} \hspace{0.15cm}\underline{= 192 \,{\rm kbit/s}} \hspace{0.05cm}.$$

(4) Die Anzahl der Steuerbit beträgt:

$$N_{\rm St} = 48 - 2 \cdot 16 -4 \hspace{0.15cm}\underline{= 12} \hspace{0.05cm}.$$

Diese sind in der Grafik gelb markiert. Die in der letzten Teilfrage berechnete Gesamt–Bruttodatenrate setzt sich somit wie folgt zusammen:

$$R_{\rm ges} = 2 \cdot {R_{\rm B}} + {R_{\rm D}} + {R_{\rm St}} = 2 \cdot 64 \,{\rm kbit/s} + 16 \,{\rm kbit/s} + 48 \,{\rm kbit/s} = 192 \,{\rm kbit/s} \hspace{0.05cm}.$$

(5)

Das Bit $b_{10} = 0$ wird dargestellt durch $U_{10} \underline{= -0.75 \ \rm V}$,
Das Bit $b_{11} = 1$ durch $U_{11} \underline{= 0 \ \rm V}$ und
Das Bit $b_{12} = 0$ durch $U_{12} \underline{= +0.75 \ \rm V}$.

Zu beachten ist, dass die erste „0” mit positiver Polarität codiert wird und alle folgenden alternierend mit $±0.75 \ {\rm V}$:

$U_{1} = U_{5} = U_{9} = U_{12} =\text{ ...} = +0.75 \ {\rm V},$
$ U_{2} = U_{7} = U_{10} = U_{13} = \text{ ...} = -0.75 \ {\rm V}$.

(6) Das L–Bit hat die Aufgabe, das AMI–codierte Signal (über alle 48 Ternärsymbole) gleichsignalfrei zu halten.

Da 22 mal das Binärsymbol „0” aufgetreten ist (also je 11 mal die Spannungswerte $+0.75 \ \rm V$ und $-0.75 \ \rm V$) und dementsprechend 27 mal das Binärsymbol „1” (Spannungswert $0 \ \rm V$), ist $U_{48}\hspace{0.15cm}\underline{=0 \ \rm V}$ zu setzen.