Aufgabe 2.7Z: Leistungsdichtespektren der Pseudoternärcodes

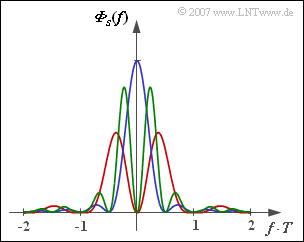
Leistungsdichtespektren von drei verschiedenen Pseudoternärcodes

In der Grafik sehen Sie die Leistungsdichtespektren von drei verschiedenen Pseudoternärcodes, die sich aus der allgemeinen Beschreibung gemäß der Aufgabe 2.7 durch unterschiedliche Werte der Parameter $N_{\rm C}$ und $K_{\rm C}$ ergeben. In verschiedenen Farben sind die Leistungsdichtespektren

${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$

für folgende Varianten dargestellt:

AMI–Code $(N_{\rm C} = 1, K_{\rm C} = +1)$ ,
Duobinärcode $(N_{\rm C} = 1, K_{\rm C} = -1)$ ,
Bipolarcode zweiter Ordnung $(N_{\rm C} = 2, K_{\rm C} = +1)$ .

Bei obiger LDS–Gleichung ist die Verwendung von rechteckförmigen NRZ–Sendegrundimpulsen vorausgesetzt.

Alle hier betrachteten Pseudoternärcodes besitzen die gleiche Wahrscheinlichkeitsverteilung:

${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$

Hinweise:

Die Aufgabe gehört zum Kapitel Symbolweise Codierung mit Pseudoternärcodes.

Sie können die Ergebnisse mit dem interaktiven Applet Signale, AKF und LDS der Pseudoternärcodes überprüfen.

Fragebogen

Musterlösung

(1) Beim AMI–Code kann das LDS wie folgt umgeformt werden:

${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$

Dieser Kurvenverlauf ist rot dargestellt. Das LDS der Amplitudenkoeffizienten ist ${\it \Phi}_{a}(f) = \sin^2(\pi fT)$ .

(2) Nach Umformung erhält man für den Duobinärcode:

${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \cos^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$

In der Grafik ist der Duobinärcode blau gezeichnet. Weiterhin gilt ${\it \Phi}_{a}(f) = \cos^2(\pi fT)$ .

(3) Der Bipolarcode zweiter Ordnung unterscheidet sich vom AMI–Code nur durch den Faktor $2$ im Argument der $\sin^{2}$ –Funktion:

${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (2\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$

Der grüne Kurvenzug stellt diesen Funktionsverlauf dar. Gegenüber dem AMI-Code ist ${\it \Phi}_{a}(f)$ genau halb so breit.

(4) Die Sendeleistung $P_{\rm S}$ ist gleich dem Integral über das Leistungsdichtespektrum ${\it \Phi}_{s}(f)$ und ist für alle hier betrachteten Codes gleich ⇒ Lösungsvorschlag 4.

Dies folgt auch aus der Leistungsberechnung durch Scharmittelung:

$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$

(5) Richtig sind die Lösungsvorschläge 1 und 3:

Gleichsignalfreiheit liegt vor, wenn das Leistungsdichtespektrum bei der Frequenz $f = 0$ keinen Anteil aufweist.
Dies gilt für den AMI–Code und den Bipolarcode zweiter Ordnung.
Diese Aussage bedeutet nicht nur, dass $s(t)$ keinen Gleichanteil besitzt, also dass ${\it \Phi}_{s}(f)$ keine Diracfunktion bei $f = 0$ besitzt.
Es bedeutet darüber hinaus auch, dass der kontinuierliche LDS–Anteil bei $f = 0$ verschwindet.
Dies wird genau dann erreicht, wenn sowohl die lange „ $+1$ ”– als auch die lange „ $–1$ ”–Folge durch die Codiervorschrift ausgeschlossen werden.

(6) Beide vorgegebenen Lösungsvorschläge treffen in der Praxis zu.

	AMI–Code,
	Duobinärcode,
	Bipolarcode 2. Ordnung.
	Die Sendeleistung ist bei allen Codes gleich.

	Zur Verbindung von Leitungen unterschiedlicher Impedanz braucht man Übertrager. Diese haben Hochpasscharakter.
	Da die Stromversorgung oft über die Signalleitung erfolgt, darf das Nachrichtensignal keinen Gleichsignalanteil beinhalten.

	rot,
	blau,
	grün.

	rot,
	blau,
	grün.

	rot,
	blau,
	grün.