Aufgabe 1.3Z: Nochmals Rayleigh–Fading?
Aus LNTwww
Version vom 11. Mai 2020, 09:32 Uhr von Guenter (Diskussion | Beiträge)
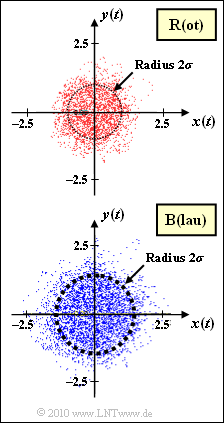
Dargestellt ist der multiplikative Faktor $z(t) = x(t) + {\rm j} \cdot y(t)$ zweier Mobilfunkkanäle $($beide ohne Mehrwegeausbreitung$)$ in 2D–Darstellung. Als gesichert wird vorgegeben:
- Der Kanal $\rm R$ $($die Bezeichnung ergibt sich aus der Farbe „Rot” der Punktwolke$)$ ist rayleighverteilt mit $\sigma_{\rm R} = 0.5$.
- Für die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ von Betrag $a(t) = |z(t)|$ bzw. Betragsquadrat $p(t) = |z(t)|^2$ gelten somit die folgenden Gleichungen $($mit $\sigma = \sigma_{\rm R})$:
- $$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm},$$
- $$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^{ -{p}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} .$$
- Vom Kanal $\rm B$ $($„Blau”$)$ ist nur die Punktwolke gegeben. Es ist abzuschätzen, ob hier ebenfalls Rayleigh–Fading vorliegt, und wenn $\rm JA$, wie groß bei diesem Kanal die Kenngröße $\sigma = \sigma_{\rm B}$ ist.
- In der Teilaufgabe (3) wird schließlich auch auf die WDF $f_{\it \phi}(\phi)$ der Phasenfunktion $\phi(t)$ Bezug genommen. Diese ist wie folgt definiert:
- $$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Wahrscheinlichkeitsdichte des Rayleigh–Fadings dieses Buches.
- Eine ähnliche Thematik wird mit anderer Herangehensweise im Kapitel Weitere Verteilungen des Buches „Stochastische Signaltheorie” behandelt.
- Zur Überprüfung Ihrer Ergebnisse können Sie das interaktive Applet WDF, VTF und Momente spezieller Verteilungen benutzen.
Fragebogen
Musterlösung
(1) Richtig ist JA:
- Man erkennt auch hier die Rotationssymmetrie, wenn man berücksichtigt, dass hier nur $N = 10\hspace{0.05cm}000$ Abtastwerte in der komplexen Ebene dargestellt wurden.
- Außerdem hätten bei NEIN die nachfolgenden Fragen keinen Sinn.
(2) Durch Vermessen der beiden eingezeichneten Kreise erkennt man:
- Beim „blauen” Kanal sind die Streuungen von Real– und Imaginärteil um etwa den Faktor 1.4 $($exakt: $\sqrt{2})$ größer als beim „roten” Kanal:
- $$\sigma_{\rm B} = \sigma_{\rm R} \cdot \sqrt{2} = 0.5 \cdot \sqrt{2}= {1}/{\sqrt{2}}\hspace{0.15cm} \underline{ \approx 0.707} \hspace{0.05cm}.$$
(3) Richtig ist NEIN:
- In beiden Fällen beschreibt $f_{\it \phi}(\phi)$ eine Gleichverteilung zwischen $-\pi$ und $+\pi$.
- Die größeren Amplituden von Kanal $\rm B$ spielen für die Phasenfunktion $\phi(t)$ keine Rolle.
(4) Richtig ist der Lösungsvorschlag 2:
- Bei Rayleigh–Fading sind Realteil $x(t)$ und Imaginärteil $y(t)$ jeweils gaußverteilt.
- Die Exponentialverteilung ergibt sich für das Betragsquadrat $p(t) = |z(t)|^2$.
(5) Richtig ist hier der Lösungsvorschlag 3, wie bereits in der Musterlösung zu (4) begründet wurde.
(6) Der Betrag $a(t)$ ist rayleighverteilt. Somit gilt für die gesuchte Wahrscheinlichkeit:
- $${\rm Pr}(a > A) = \int_{A}^{\infty}\frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$$
- In einigen Formelsammlungen findet man die Lösung für dieses Integral, aber nicht in allen.
- Es gilt aber auch mit der einseitig–exponentialverteilten Zufallsgröße $p = a^2$:
- $${\rm Pr}(a > A) = {\rm Pr}(p > A^2) = \frac{1}{2\sigma^2} \cdot\int_{A^2}^{\infty} {\rm e}^{ -{p}/(2\sigma^2)} \hspace{0.15cm}{\rm d}p \hspace{0.05cm}.$$
- Dieses Integral ist elementar und liefert das Ergebnis:
- $${\rm Pr}(a > A) = {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$
- Richtig ist demnach der Lösungsvorschlag 2.
(7) Für den Kanal $\rm R$ gilt mit $\sigma = 0.5$:
- $${\rm Pr}(|z(t)| > 1) = {\rm e}^{-2} \hspace{0.15cm} \underline{ \approx 0.135} \hspace{0.05cm}.$$
- In der oberen Grafik entspricht das der Anzahl aller Punkte, die außerhalb des eingezeichneten Kreises liegen, bezogen auf die Anzahl $N = 10\hspace{0.05cm}000$ aller Punkte.
- Für den Kanal $\rm B$ gilt wegen der doppelten Varianz $\sigma^2 = 0.5$ dagegen ${\rm Pr}(|z(t)|>1) = {\rm e}^{\rm –1} \ \underline {\approx \ 0.368}$.
- Der (nicht eingezeichnete) Bezugskreis hätte auch auch in der unteren Grafik den Radius $1$.
- Der im unteren Bild eingezeichnete Kreis hat einen größeren Radius als $A = 1$, nämlich $A = \sqrt{2}\approx 1.414$.