Aufgabe 2.6: Einheiten bei GWSSUS

• Zurück zum Buch

Überblick der GWSSUS–Funktionen

Der Mobilfunkkanal kann in sehr allgemeinen Form durch vier Systemfunktionen beschrieben werden, wobei der Zusammenhang zwischen je zwei Funktionen durch

• die Fouriertransformation bzw.
• die Fourierrücktransformation

gegeben ist.

Wir bezeichnen die Funktionen einheitlich mit  $\eta_{12}$.  Die Indizes seien wie folgt vereinbart:

• $\rm V$  steht für Verzögerung  $\tau$  $($Index „1”$)$,
• $\rm F$  steht für die Frequenz  $f$  $($Index „1”$)$,
• $\rm Z$  steht für die Zeit  $t$  $($Index „2”$)$,
• $\rm D$  steht für die Dopplerfrequenz  $f_{\rm D}$  $($Index „2”$)$.

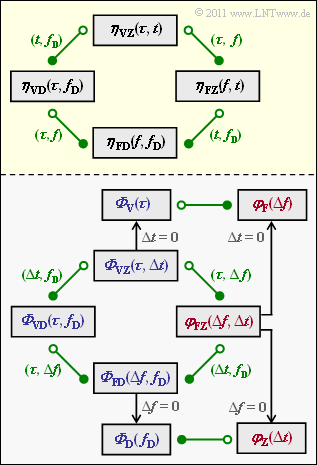
Der Zusammenhang zwischen den Funktionen ist in der oberen Grafik (gelbe Hinterlegung) dargestellt.  Die Fourierkorrespondenzen sind grün eingezeichnet:

• Der Übergang von einem weiß gefüllten zu einem grün gefüllten Kreis entspricht einer  Fouriertransformation.
• Der Übergang von einem grün gefüllten zu einem weiß gefüllten Kreis entspricht der  Fourierrücktransformation  (Gegenrichtung).

Beispielsweise gilt:

$$\eta_{\rm VZ}(\tau,\ t) \hspace{0.2cm} \stackrel{\tau, \hspace{0.08cm}f}{\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.2cm} \eta_{\rm FZ}(f,\ t)\hspace{0.05cm}, \hspace{0.4cm}\eta_{\rm FZ}(f,\ t) \hspace{0.2cm} \stackrel{f, \hspace{0.08cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} \eta_{\rm VZ}(\tau,\ t)\hspace{0.05cm}.$$

• Die hieraus abgeleitete Korrelationsfunktion  $\varphi_{12}$  und das Leistungsdichtespektrum  $\it \Phi_{\rm 12}$  werden mit den gleichen Indizes versehen wie die Systemfunktion  $\eta_{12}$.
• Korrelationsfunktionen erkennt man in der unteren Grafik an der roten Schrift, während alle Leistungsdichtespektren blau beschriftet sind.  Es wird stets vom GWSSUS–Modell ausgegangen.

Betrachten wir hier die Systemfunktion  $\eta_{\rm VZ}(\tau,\ t)$, also die zeitvariante Impulsantwort  $h(\tau,\ t)$.  Für diese ergeben sich folgende Beschreibungsgrößen:

$$\varphi_{\rm VZ}(\tau_1,\ t_1,\ \tau_2,\ t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1,\ t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2,\ t_2) \right ]\hspace{0.05cm},$$

$$\Delta \tau = \tau_2 - \tau_1 \hspace{0.05cm}, \hspace{0.2cm} \Delta t = t_2 - t_1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \varphi_{\rm VZ}(\Delta \tau,\ \Delta t) \hspace{0.05cm},$$

$$\varphi_{\rm VZ}(\Delta \tau,\ \Delta t) = \delta(\Delta \tau) \cdot {\it \Phi}_{\rm VZ}(\tau,\ \Delta t) \hspace{0.05cm}.$$

$${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau,\ \Delta t = 0)\hspace{0.05cm}.$$

Hinweis:   Die Aufgabe gehört zum Kapitel  Das GWSUS–Kanalmodell.

Fragebogen

1

Stimmen die hier angegebenen Einheiten der Systemfunktionen?

	$\eta_{\rm VZ}(\tau,\ t)$  hat die Einheit  $[1/\rm s]$.
	$\eta_{\rm FZ}(f,\ t)$  hat keine Einheit.
	$\eta_{\rm VD}(\tau,\ f_{\rm D})$  hat keine Einheit.
	$\eta_{\rm FD}(f,\ f_{\rm D})$  hat die Einheit  $[1/\rm Hz]$.

2

Stimmen die Einheiten der folgenden Funktionen?

	$\varphi_{\rm VZ}(\Delta \tau,\ \Delta t)$  hat die Einheit  $[1/\rm s]$.
	${\it \Phi}_{\rm VZ}(\tau,\ {\rm \Delta} t)$  hat die Einheit  $[1/\rm s]$.
	${\it \Phi}_{\rm V}(\tau)$  hat die Einheit  $[1/\rm s]$.

3

Stimmen die Einheiten der weiteren Funktionen?

	$\varphi_{\rm FZ}(\Delta f,\ \Delta t),   \varphi_{\rm F}(\Delta f)$  und  $\varphi_{\rm Z}(\Delta t)$  haben keine Einheit.
	${\it \Phi}_{\rm VD}(\tau,\ f_{\rm D})$  hat die Einheit  $[1/\rm s]$.
	${\it \Phi}_{\rm FD}(\Delta f,\ f_{\rm D})$  und  ${\it \Phi}_{\rm D}(f_{\rm D})$  haben jeweils die Einheit $[1/\rm Hz]$.

Musterlösung

Musterlösung

(1)  Alle Aussagen sind richtig:

• $\eta_{\rm VZ}(\tau,\ t)$  ist die zeitvariante Impulsantwort, für die auch die Bezeichnung  $h(\tau,\ t)$  gebräuchlich ist.  Wie jede Impulsantwort hat auch  $h(\tau,\ t)$  die Einheit  $[1/\rm s]$.
• Durch Fouriertransformation der Funktion  $\eta_{\rm VZ}(\tau,\ t)$  bezüglich der Verzögerung  $\tau$  kommt man zu

$$\eta_{\rm FZ}(f, t) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}.$$

• Durch die Integration nach  $\tau$  $($Einheit:  $\rm s)$  ist  $\eta_{\rm FZ}(f,\ t)$, die auch als „zeitvariante Übertragungsfunktion” bezeichnet wird, ohne Einheit.  In mancher Literatur wird anstelle von  $\eta_{\rm FZ}(f,\ t)$  auch  $H(f,\ t)$  verwendet.

• Auch die Verzögerungs–Doppler–Darstellung  $\eta_{\rm VD}(\tau,\ f_{\rm D})$  hat keine Einheit.  Diese Funktion ergibt sich aus der zeitvarianten Impulsantwort  $\eta_{\rm VZ}(\tau,\ t)$  durch die Fouriertransformation hinsichtlich  $t$:

$$\eta_{\rm VD}(\tau, f_{\rm D}) = \int_{-\infty}^{+\infty} \eta_{\rm VZ}(\tau, t) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} t}\hspace{0.15cm}{\rm d}t \hspace{0.05cm}.$$

• Die Funktion  $\eta_{\rm FD}(t,\ f_{\rm D})$  ergibt sich aus den dimensionslosen Funktionen  $\eta_{\rm VD}(\tau,\ f_{\rm D})$  bzw.  $\eta_{\rm FZ}(f,\ t)$  jeweils durch eine Fouriertransformation, was die Einheit  $[\hspace{0.03cm}\rm s\hspace{0.03cm}] = [1/\rm Hz\hspace{0.03cm}]$  zur Folge hat.

(2)  Richtig sind die Lösungsvorschläge 2 und 3:

• Die Autokorrelationsfunktion ist definitionsgemäß der folgende Erwartungswert:

$$\varphi_{\rm VZ}(\tau_1,\ t_1,\ \tau_2,\ t_2) = {\rm E} \left [ \eta_{\rm VZ}(\tau_1,\ t_1) \cdot \eta_{\rm VZ}^{\star}(\tau_2,\ t_2) \right ]\hspace{0.05cm}.$$

• Da die zeitvariante Impulsantwort  $\eta_{\rm VZ}(\tau,\ t)$  die Einheit  $[1/\rm s\hspace{0.03cm}]$  aufweist, hat deren AKF  $\varphi_{\rm VZ}$  die Einheit  $[1/\rm s^2\hspace{0.03cm}]$, sowohl mit dem Argument  $(\tau_1,\ t_1,\ \tau_2,\ t_2)$  als auch mit dem GWSSUS–Argument  $(\Delta \tau, \ \Delta t)$.

• Die Diracfunktion  $\delta(\Delta \tau)$  hat die Dimension  $[1/\rm s\hspace{0.03cm}]$, da das Integral über alle  $\tau$  $($mit Einheit  $[\rm s\hspace{0.03cm}])$  den Wert  $1$  ergeben muss.  Daraus folgt für die Verzögerungs–Zeit–Kreuzleistungsdichte  ${\it \Phi}_{\rm VZ}(\tau,\ \Delta \tau)$  die Einheit  $[1/\rm s\hspace{0.03cm}]$, ebenso für die Verzögerungs–Leistungsdichte  ${\it \Phi}_{\rm V}(\tau) = {\it \Phi}_{\rm VZ}(\tau,\ \Delta t = 0)$.

(3)  Richtig sind hier die Aussagen 1 und 3:

• Ausgehend von der Einheit  $[1/\rm s\hspace{0.03cm}]$  der Funktion  ${\it \Phi}_{\rm VZ}(\tau,\ \Delta t)$  kommt man durch Fouriertransformation bezüglich  $\tau$  bzw.  $\Delta t$  zu den Funktionen  $\varphi_{\rm FZ}(\Delta f,\ \Delta t)$  bzw.  ${\it \Phi}_{\rm VD}(\tau,\ f_{\rm D})$.  Beide sind dimensionslos.

• Das Frequenz–Doppler–Kreuzleistungsdichtespektrum hat die Einheit  $[\rm s\hspace{0.03cm}] = [1/\rm Hz\hspace{0.03cm}]$, wegen

$${\it \Phi}_{\rm FD}(\Delta f, f_{\rm D}) = \int_{-\infty}^{+\infty} {\it \Phi}_{\rm VD}(\tau, f_{\rm D}) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi f_{\rm D} \tau}\hspace{0.15cm}{\rm d}\tau \hspace{0.05cm}.$$