Aufgabe 3.4Z: GSM–Vollraten–Sprachcodec

• Zurück zum Buch

LPC-, LTP- und RPE-Parameter beim GSM-Vollraten-Codec

Dieser 1991 für das GSM–System standardisierte Codec – dieses Kunstwort steht für eine gemeinsame Realisierung von Coder und Decoder – mit der englischen Bezeichnung  $\text{GSM Fullrate Vocoder}$  kombiniert drei Methoden zur Kompression von Sprachsignalen:

• Linear Predictive Coding  $\rm (LPC)$,
• Long Term Prediction  $\rm (LTP)$, und
• Regular Pulse Excitation  $\rm (RPE)$.

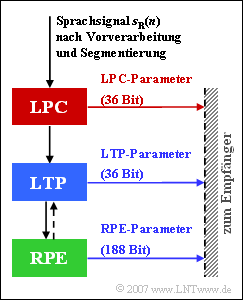
Die in der Grafik angegebenen Zahlen geben die Bitzahl an, die von den drei Einheiten dieses FR–Sprachcodecs pro Rahmen von jeweils  $20$  Millisekunden Dauer generiert werden.

Anzumerken ist dabei, dass LTP und RPE im Gegensatz zu LPC nicht rahmenweise, sondern mit Unterblöcken von  $5$  Millisekunden arbeiten.  Dies hat jedoch keinen Einfluss auf die Lösung der Aufgabe.

Das Eingangssignal in obiger Grafik ist das digitalisierte Sprachsignal  $s_{\rm R}(n)$.

Dieses entsteht aus dem analogen Sprachsignal  $s(t)$  durch

• eine geeignete Begrenzung auf die Bandbreite  $B$,
• Abtastung mit der Abtastrate  $f_{\rm A} = 8 \ \rm kHz$,
• Quantisierung mit  $13 \ \rm Bit$,
• anschließender Segmentierung in Blöcke zu je  $20 \ \rm ms$.

Auf die weiteren Aufgaben der Vorverarbeitung soll hier nicht näher eingegangen werden.

Hinweise:

• Diese Aufgabe gehört zum Kapitel  Gemeinsamkeiten von GSM und UMTS.
• Bezug genommen wird auch auf das Kapitel  Sprachcodierung  des Buches „Beispiele von Nachrichtensystemen”.

Fragebogen

1

Auf welche Bandbreite  $B$  muss das Sprachsignal begrenzt werden?

$B \ = \ $ $\ \rm kHz$

2

Aus wie vielen Abtastwerten  $(N_{\rm R})$  besteht ein Sprachrahmen? Wie groß ist die Eingangsdatenrate  $R_{\rm In}$?

$N_{\rm R} \hspace{0.18cm} = \ $ $\ \rm Abtastwerte$

$R_{\rm In} \hspace{0.15cm} = \ $ $\ \rm kbit/s$

3

Wie groß ist die Ausgangsdatenrate  $R_{\rm Out}$ des GSM-Vollraten-Codecs?

$R_{\rm Out} \ = \ $ $\ \rm kbit/s$

4

Welche Aussagen treffen hinsichtlich des Blocks „LPC” zu?

	LPC macht eine Kurzzeitprädiktion über eine Millisekunde.
	Die  $36$  LPC–Bits geben Koeffizienten an, die der Empfänger nutzt, um die LPC–Filterung rückgängig zu machen.
	Das Filter zur Kurzzeitprädiktion ist rekursiv.
	Das LPC–Ausgangssignal ist identisch mit dem Eingang  $s_{\rm R}(t)$.

5

Welche Aussagen sind hinsichtlich des Blocks „LTP” zutreffend?

	LTP entfernt periodische Strukturen des Sprachsignals.
	Die Langzeitprädiktion wird pro Rahmen einmal durchgeführt.
	Das Gedächtnis des LTP–Prädiktors beträgt bis zu  $15 \ \rm ms$.

6

Welche Aussagen treffen für den Block „RPE” zu?

	RPE liefert weniger Bit als LPC und LTP.
	RPE entfernt für den subjektiven Eindruck unwichtige Anteile.
	RPE unterteilt jeden Subblock nochmals in vier Teilfolgen.
	RPE wählt davon die Teilfolge mit der minimalen Energie aus.

Musterlösung

Musterlösung

(1)  Um das Abtasttheorem zu erfüllen, darf die Bandbreite  $B$  nicht größer als  $f_{\rm A}/2 \hspace{0.15cm}\underline{= 4 \ \rm kHz}$  sein.

(2)  Aus der gegebenen Abtastrate  $f_{\rm A} = 8 \ \rm kHz$  ergibt sich ein Abstand zwischen einzelnen Samples von  $T_{\rm A} = 0.125 \ \rm ms$.

• Somit besteht ein Sprachrahmen von  $(20 \ {\rm ms})$  aus  $N_{\rm R} = 20/0.125 = \underline{160 \ \rm Abtastwerten}$, jeweils quantisiert mit  $13 \ \rm Bit$.
• Die Datenrate beträgt somit

$$R_{\rm In} = \frac{160 \cdot 13}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 104\,{\rm kbit/s}}\hspace{0.05cm}.$$

(3)  Aus der Grafik ist ersichtlich, dass pro Sprachrahmen  $36 \ {\rm (LPC)} + 36 \ {\rm (LTP)} + 188 \ {\rm (RPE)} = 260 \ \rm Bit$  ausgegeben werden.

• Daraus berechnet sich die Ausgangsdatenrate zu

$$R_{\rm Out} = \frac{260}{20 \,{\rm ms}} \hspace{0.15cm} \underline {= 13\,{\rm kbit/s}}\hspace{0.05cm}.$$

• Der vom Vollraten–Sprachcodec erzielte Kompressionsfaktor ist somit  $104/13 = 8$.

(4)  Nur die beiden ersten Aussagen sind zutreffend:

• Die 36 LPC–Bit beschreiben insgesamt acht Filterkoeffizienten eines nichtrekursiven Filters, wobei aus der Kurzzeitanalyse acht AKF–Werte ermittelt und diese nach der so genannten Schur-Rekursion in Reflexionsfaktoren  $r_{k}$  umgerechnet werden.
• Aus diesen werden die acht LAR–Koeffizienten nach der Funktion  ${\rm ln}\big[(1 - r_{k})/(1 + r_{k})\big]$  berechnet, mit einer unterschiedlichen Anzahl an Bit quantisiert und zum Empfänger geschickt.
• Das LPC–Ausgangssignal besitzt gegenüber seinem Eingang  $s_{\rm R}(n)$  eine deutlich kleinere Amplitude, hat einen deutlich reduzierten Dynamikumfang und ein flacheres Spektrum.

(5)  Richtig sind die die Aussagen 1 und 3, nicht jedoch die zweite:

• Die LTP–Analyse und –Filterung erfolgt blockweise alle  $5 \ \rm ms$ (vierzig Abtastwerte), also viermal pro Sprachrahmen.
• Man bildet hierzu die Kreuzkorrelationsfunktion (KKF) zwischen dem aktuellen und den drei vorangegangenen Subblöcken.
• Für jeden Subblock werden dabei eine LTP–Verzögerung und eine LTP–Verstärkung ermittelt, die am besten zum Subblock passen.
• Berücksichtigt wird hierbei auch ein Korrektursignal der nachfolgenden Komponente „RPE”.
• Bei der Langzeitprädiktion ist wie bei der LPC der Ausgang gegenüber dem Eingang redundanzvermindert.

(6)  Richtig sind die Aussagen 2 und 3:

• Dass die Aussage 1 falsch ist, erkennt man schon aus der Grafik auf der Angabenseite, da  $188$  der  $260$  Ausgabebit von der RPE stammen.  Sprache wäre schon allein mit RPE (ohne LPC und LTP) verständlich.
• Zur letzten Aussage:  Die RPE sucht natürlich die Teilfolge mit der maximalen Energie.  Die RPE–Pulse sind eine Teilfolge  (13 von 40 Abtastwerte)  zu je drei Bit pro Teilrahmen von  $5 \ \rm ms$  und dementsprechend  $12 \ \rm Bit$  pro  $20 \ \rm ms$–Rahmen.
• Der „RPE–Pulse” belegt somit  $13 \cdot 12 = 156$  der  $260$  Ausgabebit.

Genaueres zum RPE–Block finden Sie auf der Seite  RPE–Codierung  des Buches „Beispiele von Nachrichtensystemen”.