Aufgabe 3.9Z: Gauß gefaltet mit Gauß
Aus LNTwww
Version vom 29. April 2021, 16:29 Uhr von Guenter (Diskussion | Beiträge)
Es soll das Faltungsergebnis zweier Gaußfunktionen ermittelt werden. Wir betrachten
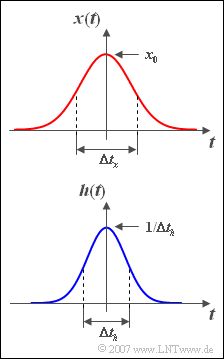
- einen gaußförmigen Eingangsimpuls x(t) mit Amplitude x0=1V und äquivalenter Dauer Δtx=4ms, sowie
- eine ebenfalls gaußförmige Impulsantwort h(t), welche die äquivalente Dauer Δth=3ms aufweist:
- x(t)=x0⋅e−π(t/Δtx)2,
- h(t)=1Δth⋅e−π(t/Δth)2.
Gesucht ist das Ausgangssignal y(t)=x(t)∗h(t), wobei der Umweg über die Spektralfunktionen gegangen werden soll.
Hinweis:
- Die Aufgabe gehört zum Kapitel Faltungssatz und Faltungsoperation.
Fragebogen
Musterlösung
(1) Durch Fouriertransformation erhält man:
- X(f)=x0⋅Δtx⋅e−π(Δtx⋅f)2,H(f)=e−π(Δth⋅f)2.
- Die gesuchten Werte sind
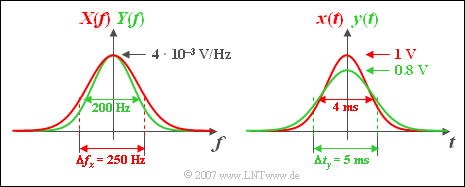
- X(f=0)=4mV/Hz_,
- H(f=0)=1_.
(2) Der Faltung im Zeitbereich entspricht die Multiplikation im Frequenzbereich:
- Y(f)=X(f)⋅H(f)=x0⋅Δtx⋅e−π(Δt2x+Δt2h)f2.
- Mit der Abkürzung Δty=(Δt2x+Δt2h)1/2=5ms kann man hierfür schreiben:
- Y(f)=x0⋅Δtx⋅e−π(Δty⋅f)2.
- Bei der Frequenz f=0 sind die Spektralwerte am Eingang und Ausgang des Gaußfilters gleich, also gilt:
- Y(f=0)=4 mV/Hz_.
- Der Funktionsverlauf von Y(f) ist schmaler als X(f) und schmaler als H(f).
(3) Es gilt die folgende Fourierkorrespondenz:
- e−π(Δty⋅f)2∙−−−∘1Δty⋅e−π(t/Δty)2.
- Damit erhält man:
- y(t)=x(t)∗h(t)=x0⋅ΔtxΔty⋅e−π(t/Δty)2.
- Der Maximalwert des Signals y(t) liegt ebenfalls bei t=0 und beträgt y0=0.8 V_.
- Die äquivalente Impulsdauer ergibt sich zu Δty=5 ms_ (siehe obiges Grafik, rechte Skizze).
- Das bedeutet: Das Gaußfilter H(f) bewirkt, dass der Ausgangsimpuls y(t) kleiner und breiter als der Eingangsimpuls x(t) ist.
- Die Impulsform bleibt weiterhin gaußförmig, weil: Gauß gefaltet mit Gauß ergibt immer Gauß!