Aufgabe 1.7: Nahezu kausaler Gaußtiefpass

Impulsantwort eines nahezu kausalen Gaußtiefpasses

Messungen haben ergeben, dass ein LZI–System mit guter Näherung durch einen Gaußtiefpass angenähert werden kann, wenn man eine zusätzliche Laufzeit $τ$ berücksichtigt. Somit lautet der Frequenzgang:

$H(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f)^2} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \tau}.$

Die beiden Systemparameter,

die äquivalente Impulsdauer $Δt = 1/Δf$ und
die Verzögerungszeit $τ$ ,

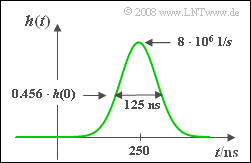
können der in der Grafik dargestellten Impulsantwort $h(t)$ entnommen werden.

Es ist offensichtlich, dass dieses Modell nicht exakt der (kausalen) Wirklichkeit entspricht, da die Impulsantwort $h(t)$ auch für $t < 0$ nicht vollkommen verschwindet.
In der Teilaufgabe (3) wird deshalb nach dem maximalen relativen Fehler gefragt, der wie folgt definiert ist:

$\varepsilon_{\rm max} = \frac{\max_{t \hspace{0.02cm}< \hspace{0.1cm}0}|h(t)|}{h(t = \tau)}.$

In Worten: Der maximale relative Fehler $ε_{\rm max}$ ist gleich dem Maximalwert der Impulsantwort $h(t)$ bei negativen Zeiten, bezogen auf den maximalen Wert $h(t = τ)$ der Impulsantwort.

Hinweise:

Die Aufgabe gehört zum Kapitel Einige systemtheoretische Tiefpassfunktionen.

Bezug genommen wird insbesondere auf die Seite Gaußtiefpass.
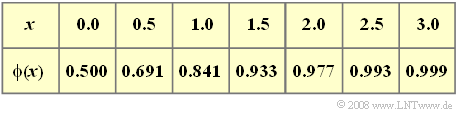
Zur Berechnung von Sprung– und Rechteckantwort können Sie das Gaußsche Fehlerintegral verwenden:

${\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$

Einige Werte der Gaußschen Fehlerfunktion

Fragebogen

$\Delta f \ = \$

$\ \rm MHz$

$\tau \ = \$

$\ \rm ns$

$y(t = 0) \ = \$

$\ \rm V$

$\varepsilon_{\rm max} \ = \$

$\ \cdot 10^{-6}$

$σ(t = 250\hspace{0.05cm} \rm ns)\ = \$

$σ(t = 300\hspace{0.05cm} \rm ns) \ = \$

Musterlösung

(1) Die äquivalente Bandbreite

$Δf$ ist gleich

$h(t = τ) \hspace{0.05cm} \rm \underline{= \ 8 \ MHz}$ .

Dies ist gleichzeitig der Kehrwert der äquivalenten Impulsdauer $Δt = 125 \ \rm ns$ .
Auch die Phasenlaufzeit $τ \hspace{0.15cm} \rm \underline{= \ 250 \ \rm ns}$ kann direkt aus der Grafik abgelesen werden.

(2) Ohne Berücksichtigung der Laufzeit ergäbe sich ein Cosinussignal mit der Amplitude

$A_y = 1\,{\rm V} \cdot {\rm e}^{-\pi({ {6\,\rm MHz} }/{ {8\,\rm MHz} })^2}= 0.171\,{\rm V}.$

Die Laufzeit bewirkt eine Phasenverschiebung um $3π$ :

$y(t) = A_y \cdot {\rm cos}(2\pi f_0 ( t - \tau) ) = A_y \cdot {\rm cos}(2\pi f_0 t - 2\pi \cdot {6\,\rm MHz}\cdot {250\,\rm ns} ) = A_y \cdot {\rm cos}(2\pi f_0 t - 3\pi ) = -A_y \cdot {\rm cos}(2\pi f_0 t ).$

Der gesuchte Wert ist somit $y(t = 0) \hspace{0.05cm} \rm \underline{= \ –0.171 \ V}$ .

(3) Die Impulsantwort lautet:

$h(t) = h_{\rm GTP}(t - \tau) =\Delta f \cdot {\rm e}^{-\pi(\frac{t - \tau}{\Delta t})^2} .$

Da $h(t)$ im Bereich $t < 0$ stetig zunimmt, tritt der Maximalwert (bei negativen Zeiten) etwa bei $t = 0$ auf:

$h(t = 0) = \Delta f \cdot {\rm e}^{-\pi(\frac{ \tau}{\Delta t})^2}= \Delta f \cdot {\rm e}^{-4\pi} .$

Mit $h(t = τ) = Δf$ erhält man so:

$\varepsilon_{\rm max}= {\rm e}^{-4\pi}\hspace{0.15cm}\underline{ \approx 3.49} \cdot 10^{-6} .$

(4) Wir lassen vorerst die Phasenlaufzeit $τ$ des zweiten Systems außer Betracht und berechnen die Sprungantwort des Gaußtiefpasses:

$\sigma_{\rm GTP}(t) = \frac{1}{\Delta t} \cdot \int_{ -\infty }^{ t } {{\rm e}^{-\pi \left({t\hspace{0.05cm}'}/{\Delta t}\right)^2}} \hspace{0.1cm}{\rm d}t'.$

Nach der Substitution $u = t\hspace{0.05cm}' \cdot {\sqrt{2\pi}}/{\Delta t}$ ergibt sich mit dem Gaußschen Fehlerintegral $ϕ(x)$ :

$\sigma_{\rm GTP}(t) = \frac{1}{\sqrt{2 \pi } } \cdot \int_{ -\infty }^{ \sqrt{2\pi}\cdot\hspace{0.05cm} t / \Delta t } { {\rm e}^{-u^2/2} } \hspace{0.1cm}{\rm d}u = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t}{\Delta t }),\hspace{1cm} {\rm \phi}(x) = \frac{1}{\sqrt{2 \pi }} \cdot \int_{ -\infty }^{ x } {{\rm e}^{-u^2/2}} \hspace{0.1cm}{\rm d}u.$

Unter Berücksichtigung der Laufzeit $τ$ erhält man somit für die gesamte Sprungantwort:

$\sigma(t) = \sigma_{\rm GTP}(t - \tau) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{t - \tau}{\Delta t }).$

Der Wert bei $t = τ = 250 \ \rm ns$ ist

$\sigma(t = {250\,\rm ns}) = \sigma_{\rm GTP}(t = 0) =\ \rm \underline{ϕ(0) \ = \ 0.500}.$

Entsprechend erhält man für $t = τ = 300 \ \rm ns$ :

$\sigma(t = {300\,\rm ns}) = \sigma_{\rm GTP}(t = {50\,\rm ns}) = {\rm \phi}(\sqrt{2\pi}\cdot \frac{ {50\,\rm ns} }{ {125\,\rm ns} })\approx {\rm \phi}(1)\hspace{0.15cm}\underline{ = 0.841}.$