Aufgabe 4.1Z: Momentenberechnung

• Zurück zum Buch

Exponentialverteilung (oben), Laplaceverteilung (unten)

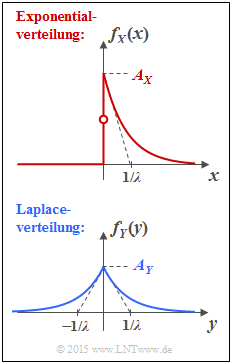
Die Grafik zeigt oben die Wahrscheinlichkeitsdichtefunktion  $\rm (WDF)$  der  Exponentialverteilung:

$$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm}x} \\ A_{ X}/2 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm}x>0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x=0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x<0. \\ \end{array}$$

Darunter gezeichnet ist die WDF der  Laplaceverteilung,  die für alle  $y$–Werte wie folgt angegeben werden kann:

$$f_Y(y) = A_{ Y} \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} |\hspace{0.03cm}y\hspace{0.03cm}|}\hspace{0.05cm}.$$

Die zwei wertkontinuierlichen Zufallsgrößen  $X$  und  $Y$  sollen hinsichtlich der folgenden Kenngrößen verglichen werden:

• dem linearen Mittelwert  $m_1$  (Moment erster Ordnung),
• dem Moment zweiter Ordnung   ⇒   $m_2$,
• der Varianz  $\sigma^2 = m_2 - m_1^2$   ⇒   Satz von Steiner,
• der Streuung  $\sigma$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Differentielle Entropie.
• Nützliche Hinweise zur Lösung dieser Aufgabe und weitere Informationen zu den wertkontinuierlichen Zufallsgrößen finden Sie im dritten Kapitel „Kontinuierliche Zufallsgrößen” des Buches  Stochastische Signaltheorie.

• Gegeben sind außerdem die beiden unbestimmten Integrale:

$$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm},$$

$$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) \hspace{0.05cm}.$$

Fragebogen

1

Wie groß ist der Maximalwert  $A_X$  der WDF  $f_X(x)$?

	$A_X = \lambda/2$,
	$A_X = \lambda$,
	$A_X = 1/\lambda$.

2

Wie groß ist der Maximalwert  $A_Y$  der WDF  $f_Y(y)$?

	$A_Y = \lambda/2$,
	$A_Y = \lambda$,
	$A_Y = 1/\lambda$.

3

Gibt es ein Argument  $z$,  so dass  $f_X(z) = f_Y(z)$  gilt?

	Ja.
	Nein.

4

Welche Aussagen gelten für die Kenngrößen der Exponentialverteilung?

	Der lineare Mittelwert ist  $m_1 = 1/\lambda$.
	Der quadratische Mittelwert ist  $m_2 = 2/\lambda^2$.
	Die Varianz ist  $\sigma^2 = 1/\lambda^2$.

5

Welche Aussagen gelten für die Kenngrößen der Laplaceverteilung?

	Der lineare Mittelwert ist  $m_1 = 1/\lambda$.
	Der quadratische Mittelwert ist  $m_2 = 2/\lambda^2$.
	Die Varianz ist  $\sigma^2 = 1/\lambda^2$.

6

Mit welcher Wahrscheinlichkeit unterscheidet sich die Zufallsgröße  $(X$  bzw.  $Y)$  vom jeweiligen Mittelwert betragsmäßig um mehr als die Streuung  $\sigma$?

$\text{Exponential:}\; \;{\rm Pr}( |X - m_X| > \sigma_X) \ = \ $

$\text{Laplace:}\; \;{\rm Pr}( |Y - m_Y| > \sigma_Y) \ = \ $

Musterlösung

Musterlösung

(1)  Richtig ist der Lösungsvorschlag 2:

• Die Fläche unter der WDF muss immer  $1$  sein.  Daraus folgt für die Exponentialverteilung:

$$A_{X} \cdot\int_{0}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = A_{X} \cdot (-1/\lambda)\cdot\big [{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\big ]_{0}^{\infty} = A_{X} \cdot (1/\lambda) \stackrel{!}{=} 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} A_{X} = \lambda \hspace{0.05cm}.$$

(2)  Richtig ist hier der Lösungsvorschlag 1:

• Aus der Grafik auf der Angabenseite erkennt man, dass die Höhe  $A_Y$  der Laplaceverteilung nur halb so groß ist wie das Maximum der Exponentialverteilung:

$$A_Y = \lambda/2.$$

(3)  Richtig ist JA, obwohl für  $z \ne 0$  stets  $f_X(z) = f_Y(z)$  gilt.  Betrachten wir nun den Sonderfall  $z= 0$:

• Für die Laplaceverteilung gilt  $f_Y(y = 0) = \lambda/2$.
• Bei der Exponentialverteilung unterscheiden sich der links- und der rechtsseitige Grenzwert für  $x \to 0$.
• Der WDF–Wert an der Stelle  $x= 0$  ist der Mittelwert dieser beiden Grenzwerte:

$$f_X(0) = \frac{1}{2} \cdot \big [ 0 + \lambda \big] = \lambda/2 = f_Y(0)\hspace{0.05cm}.$$

(4)  Richtig sind alle Lösungsvorschläge. 

Bei der Exponentialverteilung berechnet sich das Moment  $k$–ter Ordnung allgemein zu

$$m_k = \frac{k!}{\lambda^k} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} m_1 = \frac{1}{\lambda}, \hspace{0.3cm} m_2 = \frac{2}{\lambda^2}, \hspace{0.3cm} m_3 = \frac{6}{\lambda^3}, \ \text{...}$$

Somit erhält man für

• den linearen Mittelwert (Moment erster Ordnung):

$$m_1 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot \left [\frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\right ]_{0}^{\infty}= {1}/{\lambda} \hspace{0.05cm},$$

• den quadratischen Mittelwert (Moment zweiter Ordnung):

$$m_2 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) \right ]_{0}^{\infty} ={2}/{\lambda^2} \hspace{0.05cm}.$$

Daraus ergibt sich mit dem Satz von Steiner für die Varianz der Exponentialverteilung:

$$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} -{1}/{\lambda^2} = {1}/{\lambda^2} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \sigma = {1}/{\lambda}\hspace{0.05cm}.$$

Zur Verdeutlichung der Musterlösung zur Aufgabe  (5)

(5)  Richtig ist nur der Lösungsvorschlag 2:

• Der quadratische Mittelwert der Laplaceverteilung ist aufgrund der symmetrischen WDF genau so groß wie bei der Exponentialverteilung:

$$m_2 = \frac{\lambda}{2} \cdot \int_{-\infty}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|y|}\hspace{0.1cm}{\rm d}y = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y = {2}/{\lambda^2} \hspace{0.05cm}.$$

• Der Mittelwert der Laplaceverteilung ist dagegen  $m_1 = 0$.
• Damit ist die Varianz der Laplaceverteilung doppelt so groß wie bei der Exponentialverteilung:

$$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} - 0 ={2}/{\lambda^2} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \sigma = {\sqrt{2}}/{\lambda}\hspace{0.05cm}.$$

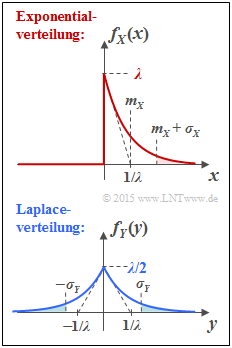
(6)  Für die Exponentialverteilung ergibt sich entsprechend der oberen Grafik mit  $m_X = \sigma_X = 1/\lambda$:

$${\rm Pr}( |X - m_X| > \sigma_X) \hspace{-0.05cm} = \hspace{-0.05cm} {\rm Pr}( X > 2/\lambda) \hspace{-0.05cm} = \hspace{-0.05cm} \lambda \cdot\int_{2/\lambda}^{\infty} \hspace{-0.08cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = -\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \right ]_{2/\lambda}^{\infty} = {\rm e}^{-2} \hspace{0.15cm}\underline {\approx 0.135}.$$

Für die Laplaceverteilung (untere Grafik) erhält man mit  $m_Y = 0$  und  $\sigma_Y = \sqrt{2}/\lambda$:

$${\rm Pr}( |Y - m_Y| > \sigma_Y) = 2 \cdot {\rm Pr}( Y > \sqrt{2}/\lambda) = 2 \cdot \frac{\lambda}{2} \cdot\int_{\sqrt{2}/\lambda}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr}( |Y - m_Y| > \sigma_Y) = \left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \right ]_{\sqrt{2}/\lambda}^{\infty} = - {\rm e}^{-\sqrt{2}} \hspace{0.15cm}\underline {\approx 0.243}\hspace{0.05cm}.$$

Ein Vergleich der schraffierten Flächen in nebenstehender Grafik bestätigt das Ergebnis qualitativ:
⇒   Die blauen Flächen sind zusammen etwas größer als die rote Fläche.