Aufgabe 3.4: Dämpfungs- und Phasenverlauf

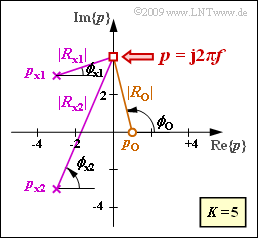
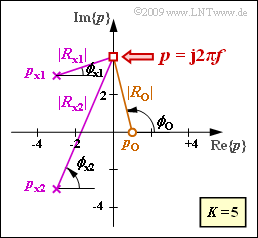
Pol–Nullstellen–Diagramm sowie Definition einiger Hilfsgrößen

Wir gehen vom skizzierten Pol–Nullstellen–Diagramm aus, also von den Werten

$K = 5, \hspace{0,2cm}Z = 1, \hspace{0,2cm}N = 2,$

$p_{\rm o}= 1,\hspace{0,2cm}p_{\rm x1}= -3 + 3{\rm j},\hspace{0,2cm}p_{\rm x2}= -3 - 3{\rm j}\hspace{0.05cm} .$

Damit lautet die $p$ –Übertragungsfunktion:

$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$

Mit der Substitution $p = {\rm j} \cdot 2 \pi f$ lässt sich die herkömmliche Übertragungsfunktion angeben, die auch als Frequenzgang bezeichnet wird:

$H(f) = H_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.05cm}.$

Aus dieser Gleichung erkennt man auch den Zusammenhang zwischen

der Übertragungsfunktion $H(f)$ ,
der Dämpfungsfunktion $a(f)$ und
der Phasenfunktion $b(f)$ .

Für eine durch den Punkt $p = {\rm j} \cdot 2 \pi f$ indirekt vorgegebene Frequenz $f$ kann man die Dämpfungs– und Phasenwerte wie folgt ermitteln:

$a(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm Np} \hspace{0.25cm} = \hspace{0.2cm} -{\rm ln} \hspace{0.1cm} K + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x1}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} ,$

$b(f)\hspace{0.15cm}{\rm in}\hspace{0.15cm}{\rm rad} \hspace{0.25cm} = \hspace{0.2cm} \phi_{\rm x1}+ \phi_{\rm x2}-\phi_{\rm o} \hspace{0.05cm} .$

Die entsprechenden Beträge $|R_{\rm o}|$ , $|R_{\rm x1}|$ und $|R_{\rm x2}|$ können Sie ebenso wie die Winkel $\phi_{\rm o}$ , $\phi_{\rm x1}$ und $\phi_{\rm x2}$ der Grafik entnehmen.

Hinweis:

Die Aufgabe gehört zum Kapitel Laplace–Transformation und p–Übertragungsfunktion.

Fragebogen

$|H(f → ∞)| \ = \$

$|H(f = 0)| \ = \$

$a(f = 0) \ = \$

$\ \rm Np$

$a(f = 2/ \pi)\ = \$

$\ \rm Np$

$a(f = 2/ \pi)\ = \$

$\ \rm dB$

$b(f = 2/ \pi)\ = \$

$\ \rm Grad$

Musterlösung

(1) Die

$p$ –Übertragungsfunktion lautet:

$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$

Zur herkömmlichen Übertragungsfunktion (zum Frequenzgang) kommt man mit der Substitution $p = {\rm j} \cdot 2 \pi f$ :

$H(f)= K \cdot \frac {{\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm o }} {({\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm x 1})({\rm j \hspace{0.05cm}2\pi \it f} - p_{\rm x 2})} = {\rm e}^{-a(f)\hspace{0.05cm}}\cdot {\rm e}^{- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.05cm} .$

Im Grenzfall $f → \infty$ ergibt sich für den Betrag, die Dämpfung und die Phase:

$\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H(f)= \frac{K}{{\rm j \hspace{0.05cm}2\pi \it f}}\hspace{0.5cm}\Rightarrow \hspace{0.5cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} |H(f)|\hspace{0.15cm}\underline {= 0} \hspace{0.5cm} \Rightarrow \hspace{0.5cm}\lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} a(f)= \infty,\hspace{0.1cm} \lim_{f \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} b(f)\underline {= {\pi}/{2}\hspace{0.1cm}(+90^\circ)} \hspace{0.01cm}.$

(2) Aus der allgemeinen Gleichung in Teilaufgabe (1) erhält man mit dem Grenzübergang $f → 0$ :

$|H(f)|$ , ,

$a(f)$ und

$b(f)$

$|H(f=0)|= -\frac {K \cdot p_{\rm o }} {p_{\rm x 1}\cdot p_{\rm x 2}} = \frac {5 \cdot 1}{ (-3 + 3{\rm j})\cdot (-3 + 3{\rm j})}= \frac {5 }{18}\hspace{0.15cm}\underline {\approx 0.278} \hspace{0.05cm} ,$

$a(f=0)=- {\rm ln} \hspace{0.1cm}\hspace{0.15cm}\underline { |H(f=0)|= 1.281\,{\rm Np }} \hspace{0.05cm} .$

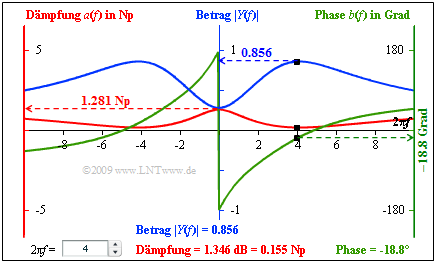
Der Bildschirmabzug des Flash–Moduls „Kausale Systeme” fasst die Ergebnisse dieser Aufgabe zusammen:

Mittlere Achse (blau): Betrag $|H(f)|$ ⇒ hier beschriftet mit $|Y(f)|$ ,
Linke Achse (rot): Dämpfung $a(f)$ ,
Rechte Achse (grün): Phase $b(f)$ .
Schwarzer Punkt: Werte für $2\pi f = 4.$

Pol–Nullstellen–Diagramm und einige Hilfsgrößen

(3) Entsprechend der detaillierten Beschreibung im Theorieteil gilt für die Dämpfungsfunktion:

$a(f)= -{\rm ln} \hspace{0.1cm} K + {\rm ln} \hspace{0.1cm} |R_{\rm x1}|+{\rm ln} \hspace{0.1cm} |R_{\rm x2}|- {\rm ln} \hspace{0.1cm} |R_{{\rm o} }|\hspace{0.05cm} .$

Zu berücksichtigen ist weiterhin die Zusatzeinheit „Neper” $\rm (Np)$ .

Gesucht ist die Dämpfung bei $f = 2/\pi$ . Dazu setzen wir $p = {\rm j} \cdot 2 \pi f = 4$ und ermitteln folgende Abstände:

$R_{\rm o} = 1 - 4 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{1^2 + 4^2}= 4.123, \hspace{1.15cm} {\rm ln} \hspace{0.1cm}|R_{\rm o}| \hspace{0.25cm} = \hspace{0.2cm}1.417\,{\rm Np }\hspace{0.05cm},$

$R_{\rm x1} = -3 - 1 \cdot {\rm j}, \hspace{0.2cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 1^2}= 3.162,\hspace{0.5cm} {\rm ln} \hspace{0.1cm}|R_{\rm x1}| \hspace{0.25cm} = \hspace{0.2cm}1.151\,{\rm Np }\hspace{0.05cm},$

$R_{\rm x2} = -3 - 7 \cdot{\rm j}, \hspace{0.2cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm} \sqrt{3^2 + 7^2}= 7.616,\hspace{0.5cm} {\rm ln} \hspace{0.1cm}|R_{\rm x2}| \hspace{0.25cm} = \hspace{0.2cm}2.030\,{\rm Np }\hspace{0.05cm}.$

$\Rightarrow \hspace{0.3cm}a(f = \frac{4}{2\pi})= -{\rm ln} \hspace{0.1cm} 5 + 1.151+ 2.030- 1.417\hspace{0.15cm}\underline{=0.155\,{\rm Np }} \hspace{0.05cm}.$

Das entspricht $0.155\ {\rm Np} \cdot 8.686 \ {\rm dB/Np} \hspace{0.15cm} \underline{= 1.346 \ {\rm dB}}$ .

(4) Nach der Beschreibung im Theorieteil gilt wegen $K > 0$ für die Phasenfunktion:

$b(f ={2}/\pi) = \phi_{\rm x1} + \phi_{\rm x2}-\phi_{\rm o}\hspace{0.05cm},$

$\phi_{\rm x1} ={\rm arctan}\hspace{0.15cm}(1/3) = 18.4^\circ\hspace{0.05cm}, \hspace{0.5cm}\phi_{\rm x2} = {\rm arctan}\hspace{0.15cm}(7/3) = 66.8^\circ\hspace{0.05cm},\hspace{0.5cm} \phi_{\rm o} = {\rm arctan}\hspace{0.15cm}(-1/4) = 180^\circ - 76^\circ = 104^\circ$

$\Rightarrow \hspace{0.3cm}b(f ={2}/\pi) = 18.4^\circ + 66.8^\circ - 104^\circ \hspace{0.15cm} \underline{= -18.8^\circ} \hspace{0.05cm}.$