Aufgabe 2.4Z: Tiefpass-Einfluss bei Synchrondemodulation
Wir betrachten das gleiche Übertragungssystem wie in Aufgabe 2.4. Es wird nun allerdings stets eine perfekte Frequenz– und Phasensynchronisation des Synchrondemodulators (SD) vorausgesetzt.
Das Quellensignal q(t), das Sendesignal s(t) sowie das Signal b(t) vor dem Tiefpassfilter innerhalb des Synchrondemodulators sind wie folgt gegeben:
- q(t)=q1(t)+q2(t)mit
- q1(t)=2V⋅cos(2π⋅2kHz⋅t),
- q2(t)=1V⋅sin(2π⋅5kHz⋅t),
- s(t)=q(t)⋅sin(2π⋅50kHz⋅t),
- b(t)=s(t)⋅2⋅sin(2π⋅50kHz⋅t).
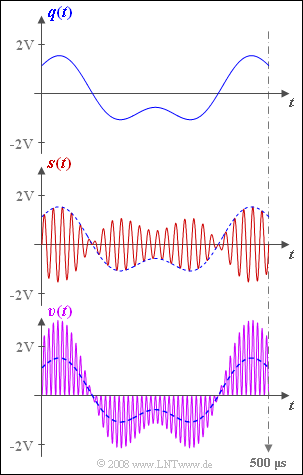
Die Grafik zeigt oben das Quellensignal q(t) und in der Mitte das Sendesignal s(t).
In der letzten Skizze ist das Sinkensignal v(t) dargestellt (violetter Kurvenverlauf).
- Dieses stimmt offensichtlich nicht mit dem Quellensignal (blau-gestrichelte Kurve) überein.
- Der Grund für das unerwünschte Ergebnis v(t)≠q(t) könnte zum Beispiel ein fehlender oder falsch dimensionierter Tiefpass sein.
In den Teilaufgaben (3) und (4) wird der so genannte Trapeztiefpass verwendet, dessen Frequenzgang wie folgt lautet:
- HE(f)={1f2−|f|f2−f10f¨urf¨urf¨ur|f|<f1,f1≤|f|≤f2,|f|>f2.
Hinweise:
- Die Aufgabe gehört zum Kapitel Synchrondemodulation.
- Bezug genommen wird insbesondere auf die Seite Blockschaltbild und Zeitbereichsdarstellung.
- Im Gegensatz zur Aufgabe 2.4 beschreiben hier f1 und f2 nicht Signalfrequenzen, sondern beziehen sich auf das Tiefpassfilter.
Fragebogen
Musterlösung
- Das dargestellte Sinkensignal v(t) stimmt exakt mit dem als Gleichung gegebenen Signal b(t) überein und enthält somit auch Anteile um die doppelte Trägerfrequenz.
- Das Filter HE(f) fehlt entweder ganz oder dessen obere Grenzfrequenz f2 ist zu hoch.
- Bezüglich der unteren Grenzfrequenz f1 ist nur die Aussage möglich, dass diese kleiner ist als die kleinste im Signal b(t) vorkommende Frequenz (2 kHz).
- Ob ein Gleichanteil durch das Filter entfernt wird oder nicht, ist unklar, da ein solcher im Signal b(t) nicht enthalten ist.
(2) Richtig sind die Aussagen 1 und 3:
- Voraussetzung für eine verzerrungsfreie Demodulation ist, dass bis zu einer bestimmten Frequenz f1 alle Spektralanteile gleich und möglichst ungedämpft übertragen werden und alle Anteile bei Frequenzen f>f2 vollständig unterdrückt werden.
- Der Rechteck– und der Trapeztiefpass erfüllen diese Bedingung.
(3) Sichergestellt werden muss, dass der 5 kHz–Anteil noch im Durchlassbereich liegt:
- f1, min=5 kHz_.
(4) Alle Spektralanteile in der Umgebung der doppelten Trägerfrequenz – genauer gesagt zwischen 95 kHz und 105 kHz – müssen vollständig unterdrückt werden:
- f2, max=95 kHz_.
- Ansonsten würde es zu nichtlinearen Verzerrungen kommen.
(5) Richtig ist der Lösungsvorschlag 2:
- Die Grenzfrequenz} fG= 4 kHz hätte (lineare) Verzerrungen zur Folge, da dann der 5 kHz–Anteil abgeschnitten würde.
- Zu bevorzugen ist der Tiefpass mit der Grenzfrequenz fG=6 kHz, da mit fG=10 kHz dem Nutzsignal v(t) mehr Rauschanteile überlagert wären.