Aufgabe 4.2Z: Korrelation zwischen „x“ und „e hoch x“

• Zurück zum Buch

Eingangs-WDF  $f_x(x)$  und Kennlinie  $y = {\rm e}^x$

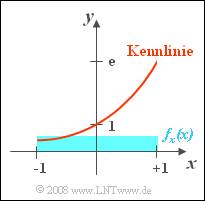
Die Zufallsgröße  $x$  sei gleichverteilt zwischen  $-1$  und  $+1$.  Damit ist

• der Mittelwert  $m_x = 0$,  und
• die Varianz  $\sigma_x^2 = 1/3$.

Durch die nichtlineare Kennlinie  $y = g(x) = {\rm e}^x$  wird die Zufallsgröße  $y$  gebildet.  Zwischen den beiden Zufallsgrößen  $x$  und  $y$  besteht also ein fester,  deterministischer Zusammenhang und die Zufallsgröße  $y$  kann nur Werte zwischen  $1/{\rm e}$  und  ${\rm e}$  annehmen.

Für die Wahrscheinlichkeitsdichtefunktion erhält man für diesen Bereich nach dem Prinzip  „Transformation von Zufallsgrößen”:

$$f_y(y) = {\rm 1}/({\rm 2\it y}).$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Zweidimensionale Zufallsgrößen.
• Bezug genommen wird auch auf das Kapitel  Erwartungswerte und Momente.
• Berücksichtigen Sie,  dass im betrachteten Bereich  $-1 ≤ x ≤ +1$  die Exponentialfunktion wie folgt angenähert werden kann:

$$y={\rm e}^{x}\approx 1+ \frac{ x}{1!} + \frac{{ x}^{\rm 2}}{\rm 2!}+ \frac{{x}^{\rm 3}}{\rm 3!}+ \frac{{x}^{\rm 4}}{\rm 4!}.$$

Fragebogen

1

Wie groß ist der Mittelwert  $m_y$  der Zufallsgröße  $y$?

$m_y \ = \ $

2

Berechnen Sie die Streuung  $\sigma_y$  der Zufallsgröße  $y$.

$\sigma_y \ = \ $

3

Welche der folgenden Aussagen gelten hinsichtlich der 2D-WDF  $f_{xy}(x, y)$?

	Außerhalb der Kurve  $y = {\rm e}^x$  ist  $f_{xy}(x, y)= 0$.
	Für alle Werte  $(x,\ {\rm e}^x)$  ist die WDF  $f_{xy}(x, y)$  konstant.
	Die WDF beschreibt eine  „Diracwand”  entlang der Kurve  $y = {\rm e}^x$.
	Die Höhe der Diraclinien nimmt von links unten nach rechts oben ab.

4

Berechnen Sie das gemeinsame Moment  $m_{xy}$  der Zufallsgrößen  $x$  und  $y$,  also den Erwartungswert des Produkts  $x \cdot y$.

$m_{xy}\ = \ $

5

Berechnen Sie den Korrelationskoeffizienten  $\rho_{xy}$  zwischen den Zufallsgrößen  $x$  und  $y$.  Interpretieren Sie das Ergebnis.

$\rho_{xy}\ = \ $

Musterlösung

Musterlösung

(1)  Der Mittelwert  $m_y$  kann in bekannter Weise aus der WDF $f_y(y)$  ermittelt werden.

• Eine zweite Berechnungsmöglichkeit basiert direkt auf den Rechenregeln für Erwartungswerte:

$$m_y={\rm E}\big[ y\big] = \int_{-\infty}^{+\infty}g(x) \cdot f_x(x)\,\, {\rm d}x = {1}/{2}\cdot\int_{-1}^{1}{\rm e}^{ x}\,\,{\rm d}x=\rm {1}/{2}\cdot(e-e^{-1}) \hspace{0.15cm}\underline{= 1.175}.$$

(2)  Für den quadratischen Mittelwert der Zufallsgröße  $y$  gilt:

$$m_{2 y} = {\rm E}\big[ y^{\rm 2}\big] = {\rm E}[{\rm e}^{ 2 x}]= {1}/{2}\cdot\int_{-1}^{+1}{\rm e}^{2 x} \,\,{\rm d}x = {1}/{4}\cdot({\rm e}^{2}-{\rm e}^{-2}) = 1.813.$$

• Daraus erhält man mit dem Satz von Steiner:

$$\sigma_y^{\rm 2} = m_{ 2 y}- m_{ y}^2 = {1}/{4}\cdot({\rm e}^{2}-{\rm e}^{-2})-{1}/{4}\cdot( {\rm e}^{2}-2+{\rm e}^{-2})={1}/{2}\cdot(1-{\rm e}^{-2})=0.432 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\sigma_y \hspace{0.15cm}\underline{= 0.658}.$$

(3)  Richtig sind  die Lösungsvorschläge 1, 3 und 4:

• Außerhalb der Kurve  $y = {\rm e}^x$  ist die WDF natürlich Null.
• Da das Volumen unter der 2D-WDF gleich  $1$  ist,  sind die WDF-Werte für den unendlich schmalen Bereich  $y = {\rm e}^x$  unendlich groß.
• Das heißt:   Die WDF beschreibt eine gekrümmte Diracwand.
• Aufgrund des Abfalls der WDF  $f_y(y)$  mit steigenden  $y$  nimmt die Höhe dieser Diracwand von  $(-1, 1/{\rm e})$  bis zu  $(+1, {\rm e})$  kontinuierlich ab.

(4)  Für das gemeinsame Moment gilt:

$$m_{xy} = {\rm E}\big[ x\cdot y \big] = {\rm E}\big[ x\cdot {\rm e}^{x} \big].$$

• Mit der angegebenen Reihenentwicklung folgt daraus die Näherung:

$$m_{xy} \approx {\rm E}\big[x\big] + {\rm E}\big[x^{\rm 2}\big] + \frac{1}{2} \cdot {\rm E}\big[ x^{\rm 3}\big] + \frac{1}{6} \cdot {\rm E}\big[ x^{\rm 4}\big]+ \frac{1}{24} \cdot {\rm E}\big[ x^{\rm 5}\big].$$

• Aufgrund der Symmetrie der Zufallsgröße  $x$  gilt für alle ungeradzahligen Werte von  $k$:   $\rm E\big[\it x^{k}\rm \big] =\rm 0.$ Weiterhin gilt:

$${\rm E}\big[ x^{\rm 2}\big] = \sigma_{x}^{\rm 2}= \frac{1}{3}, \hspace{0.5cm} {\rm E}\big[ x^{\rm 4}\big] = \frac{1}{2}\int_{-1}^{+1} x^{\rm 4} \,\,{\rm d}x = \rm\frac{1}{5}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\it m_{xy}} = \rm\frac{1}{3} + \frac{1}{6}\cdot\frac{1}{5} = \frac{11}{30}\hspace{0.15cm}\underline{\approx 0.367}.$$

(5)  Wegen  $m_x = 0$  gilt  $\mu_{xy} = m_{xy}$.  Somit ergibt sich für den Korrelationskoeffizienten:

$$\it \rho_{xy} = \frac{\mu_{xy}}{\sigma_x \cdot \sigma_y}=\rm\frac{0.367}{0.577 \cdot 0.658}\hspace{0.15cm}\underline{ \approx 0.967}.$$

• Zwischen  $x$  und  $y$  besteht zwar ein eindeutiger deterministischer Zusammenhang.
• Da aber hierin auch nichtlineare Bindungen enthalten sind, ist der Korrelationskoeffizient  $\rho_{xy} \ne 1$.