Aufgabe 4.7: Gewichtete Summe und Differenz
Die Zufallsgrößen u und v seien statistisch voneinander unabhängig, jeweils mit Mittelwert m und Varianz σ2.
- Beide Größen besitzen eine gleiche Wahrscheinlichkeitsdichtefunktion (WDF) und Verteilungsfunktion (VTF).
- Über den Verlauf dieser Funktionen sei zunächst nichts bekannt.
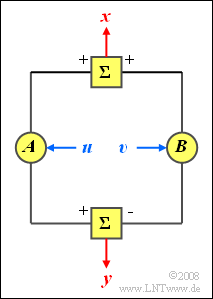
Es werden nun zwei neue Zufallsgrößen x und y entsprechend den nachfolgenden Gleichungen gebildet:
- x=A⋅u+B⋅v,
- y=A⋅u−B⋅v.
Hierbei bezeichnen A und B (beliebige) konstante Werte.
- Für die Teilaufgaben (1) bis (4) gelte m=0, σ=1, A=1 und B=2.
- Bei der Teilaufgabe (6) wird vorausgesetzt, dass u und v jeweils gaußverteilt mit Mittelwert m=1 und Streuung σ=0.5 seien. Für die Konstanten gelte hier A=B=1.
- Für die Aufgabe (7) gelte weiterhin A=B=1. Hier seien die Zufallsgrößen u und v symmetrisch zweipunktverteilt auf ±1:
- Pr(u=+1)=Pr(u=−1)=Pr(v=+1)=Pr(v=−1)=0.5.
Hinweis: Die Aufgabe gehört zum Kapitel Linearkombinationen von Zufallsgrößen.
Fragebogen
Musterlösung
- mx=(A+B)⋅m=0_.
- Für die Varianz und die Streuung gelten:
- σ2x=(A2+B2)⋅σ2=5;σx=√5≈2.236_.
(2) Da u und v die gleiche Streuung besitzen, gilt auch σy=σx≈2.236_.
- Wegen m=0 gilt zudem my=mx=0_.
- Bei mittelwertbehafteten Zufallsgrößen u und v ergäbe sich dagegen für my=(A−B)⋅m ein anderer Wert als für mx=(A+B)⋅m.
(3) Wir gehen hier in der Musterlösung von dem allgemeineren Fall m≠0 aus. Dann gilt für das gemeinsame Moment:
- mxy=E[x⋅y]=E[(A⋅u+B⋅v)(A⋅u−B⋅v)].
- Nach den allgemeinen Rechenregeln für Erwartungswerte folgt daraus:
- mxy=A2⋅E[u2]−B2⋅E[v2]=(A2−B2)(m2+σ2).
- Damit ergibt sich die Kovarianz zu
- μxy=mxy−mx⋅my=(A2−B2)(m2+σ2)−(A+B)(A−B)⋅m2=(A2−B2)⋅σ2.
- Mit σ=1, A=1 und B=2 erhält man μxy=−3_, und zwar unabhängig vom Mittelwert m der Größen u und v.
(4) Der Korrelationskoeffizient ergibt sich zu
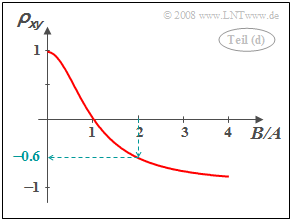
- ρxy=μxyσx⋅σy=(A2−B2)⋅σ2(A2+B2)⋅σ2⇒ρxy=1−(B/A)21+(B/A)2.
- Mit B/A=2 folgt daraus ρxy=−0.6_.
(5) Richtig sind die Aussagen 1, 3 und 4:
- Aus B=0 folgt ρxy=1 (strenge Korrelation). Man erkennt weiter, dass in diesem Fall x=u und y=u identische Zufallsgrößen sind.
- Die zweite Aussage ist nicht zutreffend: Für A=1 und B=−2 ergibt sich ebenfalls ρxy=−0.6.
- Das Vorzeichen des Quotienten spielt also keine Rolle, weil in der in der Teilaufgabe (4) berechneten Gleichung der Quotient B/A nur quadratisch auftritt.
- Ist B≫A, so werden sowohl x als auch y fast ausschließlich durch die Zufallsgröße v bestimmt und es ist y≈−x. Dies entspricht dem Korrelationskoeffizienten ρxy≈−1.
- Dagegen ergibt sich für B/A=1 stets der Korrelationskoeffizient ρxy=0 und damit die Unkorreliertheit zwischen x und y.
(6) Beide Aussagen richtig sind richtig:
- Bei A=B sind x und y stets (also bei jeder beliebigen WDF der Größen u und v) unkorreliert.
- Die neuen Zufallsgrößen x und y sind hier also ebenfalls gaußverteilt.
- Bei Gaußschen Zufallsgrößen folgt aber aus der Unkorreliertheit auch die statistische Unabhängigkeit und umgekehrt.
(7) Hier ist nur die Aussage 1 zutreffend:
- Der Korrelationskoeffizient ergibt sich mit A=B=1 auch hier zu ρxy=0. Das heißt: x und y sind auch hier unkorreliert.
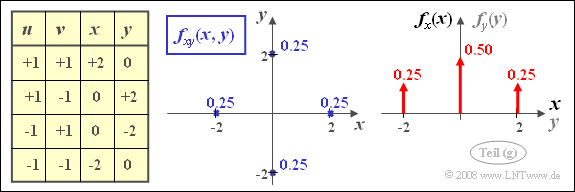
- Dagegen erkennt man aus der skizzierten 2D-WDF, dass die Bedingung der statistischen Unabhängigkeit im nun vorliegenden Fall nicht mehr gegeben ist. Vielmehr gilt nun:
- fxy(x,y)≠fx(x)⋅fy(y).