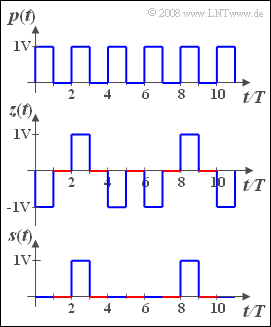
Aufgabe 4.14: AKF und KKF bei Rechtecksignalen
Wir betrachten ein periodisches Rechtecksignal p(t) entsprechend der oberen Skizze mit den beiden möglichen Amplitudenwerten 0V und 1V und der Rechteckdauer T. Die Periodendauer beträgt somit T0=2T.
Darunter ist das Zufallssignal z(t) gezeichnet.
- Dieses ist zwischen (2i−1)⋅T und 2i⋅T jeweils z(t)=0V (im Bild rot hervorgehoben).
- In den blau gezeichneten Intervallen zwischen 2i⋅T und (2i+1)⋅T ist der Signalwert zweipunktverteilt (±1V).
Die Wahrscheinlichkeit, dass in den blau dargestellten Intervallen z(t)=+1V gilt, sei allgemein gleich p und unabhängig von den vorher ausgewürfelten Werten.
Das unterste Signal in nebenstehender Grafik kann aus den beiden ersten konstruiert werden. Es gilt:
- s(t)=1/2⋅[p(t)+z(t)].
- In den rot eingezeichneten Zeitintervallen zwischen (2i−1)⋅T und 2i⋅T (i ganzzahlig) gilt s(t)=0V, da hier sowohl p(t) als auch z(t) gleich Null sind.
- In den dazwischen liegenden Intervallen ist der Amplitudenwert zweipunktverteilt zwischen 0V und 1V, wobei der Wert 1V wieder mit der Wahrscheinlichkeit p auftritt.
- Oder anders ausgedrückt: Die Signale z(t) und s(t) sind äquivalente Mustersignale des identischen Zufallsprozesses mit bipolarer (−1V, +1V) bzw. unipolarer (0V, 1V) Signaldarstellung.
Hinweise:
- Die Aufgabe gehört zum Kapitel Kreuzkorrelationsfunktion und Kreuzleistungsdichte.
- Bezug genommen wird auch auf das Kapitel Autokorrelationsfunktion.
- Skizzieren Sie die gesuchten Korrelationsfunktionen jeweils im Bereich von −7T bis +7T.
Fragebogen
Musterlösung
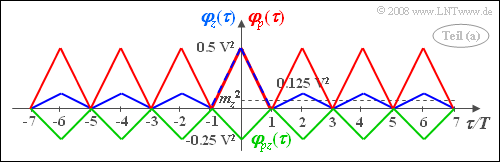
- φz(τ=0)=1/2⋅(1V)2=0.5V2_.
- Für τ=±T, τ=±3T_, ... ergibt sich φz(τ)=0_.
- Für die Zwischenwerte τ=±2T, τ=±4T, τ=±6T_, ... gilt:
- φz(τ)=1V22(p⋅p+p⋅(p−1)+(p−1)⋅p+(p−1)⋅(p−1))=...=0.5V2⋅(1−2p)2.
- Hierbei steht p für p⋅(+1) und (p−1) für (1−p)⋅(−1), also jeweils Wahrscheinlichkeit mal normierter Amplitudenwert.
- Mit p=0.25 erhält man φz(τ=±6T)=0.125V2_.
Die blaue Kurve zeigt φz(τ) für p=0.25 im Bereich von −7T≤τ≤+7T:
- Aufgrund des rechteckförmigen Signalverlaufs ergibt sich eine Summe von Dreieckfunktionen.
- Für p=0.5 würden die äußeren (kleineren) Dreiecke verschwinden.
(2) Die AKF φp(τ) des unipolaren periodischen Signals p(t) ist in der allgemeingültigen Darstellung von (1) ⇒ AKF φz(τ) als Sonderfall für p=1 enthalten.
- Man erhält nun eine periodische AKF (siehe roter Kurvenverlauf in obiger Skizze) mit
- φp(τ=0)=φp(τ=±2T)=φp(τ=±4T)=...=0.5V2_,
- φp(τ=±T)=φp(τ=±3T)=...=0_.
(3) Auch für die Kreuzkorrelationsfunktion ergibt sich für τ=±T, τ=±3T_, ... stets der Wert Null.
- Dagegen sind die KKF-Werte für τ=±2T, τ=±2T, ... identisch mit denen bei τ=0:
- φpz(τ=0)=φpz(τ=±2T)=φpz(τ=±4T)=...=1V22(p−(1−p))=2p−12V2.
- Man erhält mit p=0.25 folgende Ergebnisse (siehe grüne Kurve in obiger Skizze):
- φpz(τ=0)=−0.25V2_,φpz(τ=3T)=0_,φpz(τ=6T)=−0.25V2_.
- Mit p=1 würde dagegen z(t)≡p(t) gelten und damit natürlich auch φpz(τ)≡φp(τ)≡φz(τ).
- Für den Sonderfall p=0.5 ergäbe sich keine Korrelation zwischen p(t) und z(t) und damit φpz(τ)≡0.
(4) Durch Einsetzen von c(t)=a(t)+b(t) in die allgemeine AKF-Definition erhält man:
- φc(τ)=¯c(t)⋅c(t+τ)=¯a(t)⋅a(t+τ)+¯a(t)⋅b(t+τ)+¯b(t)⋅a(t+τ)+¯b(t)⋅b(t+τ).
- ⇒φc(τ)=φa(τ)+φab(τ)+φba(τ)+φa(τ).
- Richtig ist somit der Lösungsvorschlag 2.
- Der Lösungsvorschlag 1 trifft nur zu, wenn a(t) und b(t) unkorreliert sind.
- Der letzte Vorschlag, die Faltungsoperation, ist immer falsch.
- Eine ähnliche Gleichung würde sich nur dann ergeben, wenn wir die WDF fc(c) der Summe c(t)=a(t)+b(t) betrachten und a(t) und b(t) statistisch unabhängig sind:
- fc(c)=fa(a)⋆fb(b).
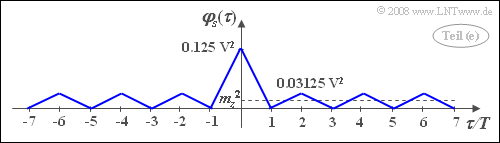
(5) Mit dem Ergebnis aus (4) und unter Berücksichtigung des Faktors 1/2 erhält man:
- φs(τ)=1/4⋅[φp(τ)+φz(τ)+2⋅φpz(τ)].
- Hierbei ist bereits berücksichtigt, dass die KKF zwischen p(t) und z(t) eine gerade Funktion ist, so dass auch φpz(τ)=φzp(τ) gilt.
- Für τ=0 erhält man deshalb mit den obigen Ergebnissen allgemein:
- φs(τ=0)=1/4⋅(0.5V2+0.5V2+2⋅2p−12V2).
- Mit p=0.25 ergibt sich φpz(τ=0)=0.125V2. Das Ergebnis ist plausibel. Im Mittel ist nur in jedem achten Intervall s(t)=1V; sonst ist s(t)=0V.
- Für geradzahlige Vielfache von T gilt:
- φs(τ=±2T)=φs(τ=±4T)= ...=0.5V24((1−2p)2+1+2⋅(2p−1))=0.5V2⋅p2.
- Mit p=0.5 erhält man hierfür den Wert 0.03125V2. Alle AKF-Werte bei ungeradzahligen Vielfachen von T sind wieder Null.
- Damit ergibt sich der unten skizzierte AKF–Verlauf.
- Die gesuchten Zahlenwerte sind somit:
- φs(τ=0)=0.125V2_,
- φs(τ=3T)=0_,
- φs(τ=6T)=−0.03125V2_.
- Ein Vergleich mit der Skizze zur Teilaufgabe (1) zeigt, dass das Binärsignal s(t) bis auf den Faktor 1/4 die gleiche AKF aufweist wie das Ternärsignal z(t).