Aufgabe 1.7: Systemwirkungsgrade

• Zurück zum Buch

Sendegrundimpuls „Trapez”

Der Empfänger eines binären Nachrichtenübertragungssystems mit Symboldauer  $T$  besteht aus einem Integrator,  der durch die Impulsantwort

$$h_{\rm E}(t) = \left\{ \begin{array}{c} 1/T \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} \hspace{0.05cm}|t| < T/2 \hspace{0.05cm}, \\ |t| > T/2 \\ \end{array}$$

beschreibbar ist.  Danach folgt ein Schwellenwertentscheider mit optimalen Parametern.

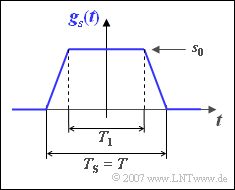
Der Sendegrundimpuls  $g_{s}(t)$  gemäß der Grafik sei im Allgemeinen trapezförmig und wird durch die Zeit  $T_{1}$  parametrisiert:

• Für  $T_{1} = 0$  ergibt sich ein Dreieckimpuls,  für  $T_{1} = T$  das NRZ–Rechteck.
• Die absolute Impulsdauer  $T_{\rm S}$  ist stets gleich der Symboldauer  $T$,   also dem Abstand zweier Sendeimpulse.

Das Signal–zu–Rausch–Leistungsverhältnis  $\rm (SNR)$  vor dem Schwellenwertentscheider kann unter der Voraussetzung,  dass keine Impulsinterferenzen auftreten,  wie folgt berechnet werden:

$$\rho_d = {g_0^2}/{\sigma_d^2}\hspace{0.05cm}.$$

Hierbei ist  $g_{0} = g_{d}(t = 0)$  der Maximalwert des Detektionsgrundimpulses und

$$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty}|h_{\rm E}(t)|^2 \,{\rm d} t = \frac{N_0}{2 \cdot T}$$

die Rauschleistung nach dem Empfangsfilter bei AWGN–Rauschen an seinem Eingang.

Im Laufe dieser Aufgabe werden folgende Größen verwendet:

• $\rho_{d,\rm\hspace{0.08cm} max \hspace{0.05cm}|\hspace{0.05cm} L}$  ist das maximale SNR unter der Nebenbedingung der Leistungsbegrenzung.
• $\rho_{d,\rm\hspace{0.08cm} max \hspace{0.05cm}|\hspace{0.05cm} A}$  ist das maximale SNR bei Spitzenwertbegrenzung  ("Amplitudenbegrenzung").

Mit diesen Definitionen lassen sich die Systemwirkungsgrade angeben:

$$\eta_{\rm L} = \ \frac{\rho_d}{\rho_{d, \hspace{0.08cm}{\rm max \hspace{0.05cm}|\hspace{0.05cm} L}}}\hspace{0.05cm},$$

$$\eta_{\rm A} = \ \frac{\rho_d}{\rho_{d, \hspace{0.08cm}{\rm max\hspace{0.05cm} | \hspace{0.05cm} A}}} = {1}/{C_{\rm S}^2}\cdot \eta_{\rm L} \hspace{0.05cm}.$$

Hierbei bezeichnet der  "Crestfaktor"  $C_{\rm S}$  das Verhältnis zwischen dem Maximalwert und dem Effektivwert (Wurzel aus der Leistung) des Sendesignals  $s(t)$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  "Optimierung der Basisbandübertragungssysteme".

• Verwenden Sie zur Lösung der Aufgabe folgende Zahlenwerte:

$$s_0^2 = 10\,{\rm mW},\hspace{0.2cm}T = 3\,{\rm{ µ s}}, \hspace{0.2cm}N_0 = 3 \cdot 10^{-10}\,{\rm W/Hz}\hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie die Impulsenergie  $E_{\rm B}$  in Abhängigkeit von  $T_{1}$.  Welche Werte ergeben sich für  $T_{1} = 0$ ,  $T_{1} = T/2$  und  $T_{1} = T$?

$T_{1} = 0\text{:} \hspace{0.75cm} E_{\rm B} \ = \ $ $\ \cdot 10^{-8} \, \rm Ws$

$T_{1} = T/2\text{:}\hspace{0.2cm} E_{\rm B} \ = \ $ $\ \cdot 10^{-8} \, \rm Ws$

$T_{1} = T\text{:}\hspace{0.65cm} E_{\rm B} \ = \ $ $\ \cdot 10^{-8} \, \rm Ws$

2

Welcher Wert  $T_{1}$  führt bei Leistungsbegrenzung zum maximal möglichen SNR?

$T_{1}/T \ = \ $

3

Wie groß ist somit das maximale SNR bei Leistungsbegrenzung?

$\rho_{d,\hspace{0.05cm}\rm max \hspace{0.05cm}|\hspace{0.05cm} L} \ = \ $

4

Wie groß ist der Detektionsgrundimpuls  $g_{d}(t)$  in Impulsmitte für  $T_{1} = T/2$?

$g_{0} \ = \ $ $\ \rm \sqrt{W}$

5

Berechnen Sie den Systemwirkungsgrad  $\eta_{\rm L}$  bei Leistungsbegrenzung  $(T_{1} = T/2)$.

$\eta_{\rm L} \ = \ $

6

Berechnen Sie den Crestfaktor  $(T_{1} = T/2)$.

$C_{\rm S} \ = \ $

7

Berechnen Sie den Systemwirkungsgrad bei Spitzenwertbegrenzung  $(T_{1} = T/2)$.

$\eta_{\rm A} \ = \ $

Musterlösung

Musterlösung

(1)  Zur Vereinfachung der Berechnungen setzen wir  $T_1' = T_1/2$  und  $T_2' = (T – T_1)/2$.

• Damit ergibt sich für die Sendeimpulsenergie:

$$E_{\rm B} = \int_{-\infty}^{+\infty}g_s^2(t) \,{\rm d} t = 2 \cdot \int_{0}^{T_1\hspace{0.0cm}'}g_s^2(t) \,{\rm d} t\hspace{0.2cm}+ \hspace{0.2cm}2 \cdot \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t \hspace{0.05cm}.$$

• Entsprechend dieser Aufteilung kann auch geschrieben werden:

$${E_{\rm B}}/{2} = s_0^2 \cdot T_1\hspace{0.0cm}' + E_2 \hspace{0.05cm},\hspace{0.3cm}{\rm mit}\hspace{0.3cm} E_{\rm 2} = \ \int_{T_1\hspace{0.0cm}'}^{T/2}g_s^2(t) \,{\rm d} t = s_0^2 \cdot \int_{0}^{T_2\hspace{0.0cm}'}\left ( 1 - \frac {t}{T_2\hspace{0.0cm}'}\right )^2 \,{\rm d} t$$

$$\Rightarrow \hspace{0.3cm}E_{\rm 2} = \ s_0^2 \cdot \left [ \int_{0}^{T_2\hspace{0.0cm}'}\,\,{\rm d} t- \frac {2}{T_2\hspace{0.0cm}'} \cdot \int_{0}^{T_2\hspace{0.0cm}'}t \,\,{\rm d} t + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot \int_{0}^{T_2\hspace{0.0cm}'}t^2 \,\,{\rm d} t\right ] = \ s_0^2 \cdot \left [ {T_2\hspace{0.0cm}'} - \frac {2}{T_2\hspace{0.0cm}'} \cdot \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^2}{2} + \frac {1}{(T_2\hspace{0.0cm}'\hspace{0.02cm})^2} \cdot \frac {(T_2\hspace{0.0cm}'\hspace{0.02cm})^3}{3}\right ] = s_0^2 \cdot\frac {T_2\hspace{0.0cm}'\hspace{0.02cm}}{3} \hspace{0.05cm}.$$

• Eingesetzt in obige Gleichung erhält man:

$${E_{\rm B}}/{2} = s_0^2 \cdot \frac {T_1}{2}+ s_0^2 \cdot \frac {T-T_1}{2 \cdot 3}= s_0^2 \cdot \left [\frac{T}{6} + \frac{T_1}{3}\right ]\hspace{0.3cm} \hspace{0.3cm}\Rightarrow E_{\rm B} = {s_0^2}/{3}\cdot \left (T + 2 \cdot T_1 \right )\hspace{0.05cm}.$$

• Mit den angegebenen Werten  ${s_{0}}^{2} = 10 \ \rm mW$  und  $T = 3\ \rm µ s$  erhält man:

$$T_1 = 0\text{:} \hspace{0.75cm} {E_{\rm B}} = \ 1/3 \cdot{s_0^2 \cdot T}= 1/3 \cdot {10^{-2}\,{\rm W} \cdot 3 \cdot 10^{-6}\,{\rm s}} \hspace{0.1cm}\underline {= 1 \cdot 10^{-8}\,{\rm Ws}}\hspace{0.05cm},$$

$$T_1 = T/2\text{:} \hspace{0.2cm} {E_{\rm B}} = \ 2/3 \cdot{ s_0^2 \cdot T}= \hspace{2.6cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 2 \cdot 10^{-8}\,{\rm Ws}} \hspace{0.05cm},$$

$$T_1 = T\text{:} \hspace{0.65cm} {E_{\rm B}} = \ { s_0^2 \cdot T}= \hspace{3.65cm}\text{...} \hspace{1.4cm}\hspace{0.1cm}\underline {= 3 \cdot 10^{-8}\,{\rm Ws}} \hspace{0.05cm}.$$

(2)  Der Systemwirkungsgrad bei Leistungsbegrenzung ist maximal  $(\eta_{\rm L} = 1)$,  wenn der Sendegrundimpuls  $g_{s}(t)$  formgleich mit der Impulsantwort  $h_{\rm E}(t)$ ist. 

• Dies trifft hier für den NRZ–Sendeimpuls zu:   $T_1/T \ \underline{= 1}$.

(3)  Unter der in Teilaufgabe  (2)  genannten Bedingung erhält man das maximale SNR:

$$\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm}| \hspace{0.05cm} L}}= \frac{2 \cdot E_{\rm B}}{N_0} = \frac{2 \cdot 3 \cdot 10^{-8}\,{\rm Ws}}{3 \cdot 10^{-10}\,{\rm W/Hz}}\hspace{0.1cm}\underline {= 200} \hspace{0.05cm}.$$

(4)  Allgemein gilt  $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$.  Für  $t = 0$  ergibt sich  mit  $T_1 = T/2$  hierfür die Trapezfläche:

$$g_0 = g_d(t=0) = \frac{1}{T} \cdot \int_{-\infty}^{+\infty}g_s(t) \,{\rm d} t = \frac{T + T_1}{2} \cdot s_0 = 0.75 \cdot 0.1 \cdot \sqrt{\rm W} \hspace{0.1cm}\underline {= 0.075 \,\sqrt{\rm W}} \hspace{0.05cm}.$$

(5)  Mit  $T_1 = T/2$  (trapezförmige Sendeimpulse)  erhält man für das Signal–zu–Rausch–Verhältnis:

$$\rho_d = \frac{g_0^2}{\sigma_d^2}\hspace{0.3cm}{\rm mit}\hspace{0.3cm} g_0^2=0.075^2\, {\rm W},\hspace{0.1cm} \sigma_d^2 = \frac{N_0}{2 \cdot T} = 5 \cdot 10^{-5}\,{\rm W}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\rho_d = \frac{0.075^2\, {\rm W}}{5 \cdot 10^{-5}\,{\rm W}} = 112.5 \hspace{0.05cm}.$$

• Somit ergibt sich für den Systemwirkungsgrad bei Leistungsbegrenzung mit dem Ergebnis aus  (3):

$$\eta_{\rm L} = \frac{\rho_d}{\rho_{d, \hspace{0.05cm}{\rm max \hspace{0.05cm} | \hspace{0.05cm} L}}}= \frac{112.5}{200}\hspace{0.1cm}\underline {= 0.5625 }\hspace{0.05cm}.$$

• Aufgrund der Fehlanpassung ist $\eta_{\rm L} < 1$.

(6)  Mit dem Maximalwert  $s_{0}$  und dem Ergebnis der Teilaufgabe  (1)  gilt:

$$s_{\rm eff} = \sqrt{{ E_{\rm B}}/{T}}= \sqrt{{ 2/3 \cdot s_{0}^2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}C_{\rm S} ={ s_{\rm 0}}/{s_{\rm eff}}= \sqrt{{ 3}/{2}}\hspace{0.1cm}\underline { \approx 1.225}\hspace{0.05cm}.$$

(7)  Der Systemwirkungsgrad bei Spitzenwertbegrenzung ist kleiner als der bei Leistungsbegrenzung,
          da hier neben der Fehlanpassung auch das nicht optimale Sendesignal (zu kleine Energie) eine Rolle spielt:

$$\eta_{\rm A} = \frac{1}{C_{\rm S}^2}\cdot \eta_{\rm L} = \frac{ 2}{3} \cdot 0.5625 =\hspace{0.1cm}\underline { 0.375} \hspace{0.05cm}.$$