Entscheidungsrückkopplung

1. Digitalsignalübertragung
2. Impulsinterferenzen und Entzerrungsverfahren
3. Entscheidungsrückkopplung

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Prinzip und Blockschaltbild

Eine Möglichkeit zur Verminderung von Impulsinterferenzen bietet die  Entscheidungsrückkopplung  (engl.:  "Decision Feedback Equalization"  $\rm (DFE)$.  In der deutschsprachigen Literatur wird diese manchmal auch als  "Quantisierte Rückkopplung"  $\rm (QR)$  bezeichnet.

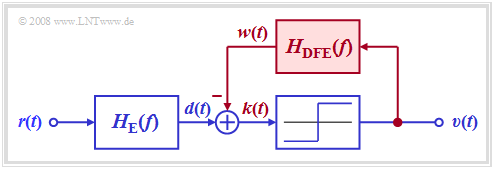
Die Grafik zeigt den entsprechenden Empfänger.  Man erkennt anhand des Blockschaltbildes:

Empfänger mit Entscheidungsrückkopplung  $\rm (DFE)$

• Ohne die rot eingezeichnete Signalrückführung ergäbe sich ein herkömmlicher Digitalempfänger mit Schwellenwertentscheidung entsprechend dem Kapitel  "Idealer Kanalentzerrer".

• Für die folgende Beschreibung wird wieder angenommen,  dass sich das gesamte Empfangsfilter  $H_{\rm E}(f)$  aus dem (fiktiven) idealen Kanalentzerrer  $1/H_{\rm K}(f)$  und einem Gaußtiefpass  $H_{\rm G}(f)$  zur Rauschleistungsbegrenzung zusammensetzt.
  

• Beim Empfänger mit Entscheidungsrückkopplung wird vom rechteckförmigen Ausgangssignal  $v(t)$  über ein lineares Netzwerk mit dem Frequenzgang  $H_{\rm DFE}(f)$  ein Kompensationssignal  $w(t)$  gewonnen und an den Eingang des Schwellenwertentscheiders zurückgeführt.
  

• Dieses Signal  $w(t)$  wird vom vorentzerrten Signal  $d(t)$  subtrahiert. Bei geeigneter Dimensionierung des Rückkopplungsnetzwerkes weist somit das  korrigierte Signal  $k(t) = d(t) - w(t)$ keine  (oder zumindest deutlich geringere)  Impulsnachläufer auf als das Signal  $d(t)$.  Im Gegensatz zu diesen Impulsnachläufern können die Impulsvorläufer aus Kausalitätsgründen nicht beeinflusst werden.
  

• Da bei diesem Empfänger mit Entscheidungsrückkopplung das Kompensationssignal  $w(t)$  vom rauschfreien Sinkensignal  $v(t)$  abgeleitet wird,  ist die Signalentzerrung nicht mit einer Erhöhung der Rauschleistung verbunden wie bei linearer Entzerrung.  Vielmehr besitzt das korrigierte Signal  $k(t)$  den gleichen Rauscheffektivwert  $\sigma_d$  wie das Signal  $d(t)$.
  
  

Hinweise:

(1)   Die Signalverläufe dieses nichtlinearen DFE–Entzerrungsverfahrens  sowie die zugehörigen Fehlerwahrscheinlichkeiten – gültig für einen verzerrungsfreien Kanal – können mit dem interaktiven SWF–Applet  "Entscheidungsrückkopplung"  angezeigt werden.

(2)   Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im

Versuch 3: Impulsinterferenzen und Entzerrung,     Programm „qrk”

des Praktikums „Simulation digitaler Übertragungssysteme” [Söd01]. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf

• dem Lehrsoftwarepaket  LNTsim  ⇒  Link verweist auf die ZIP-Version des Programms und
• dieser Praktikumsanleitung  ⇒  Link verweist auf die PDF-Version (82 Seiten).

Ideale Entscheidungsrückkopplung

Wir behandeln zunächst die ideale DFE–Realisierung anhand der Grundimpulse.

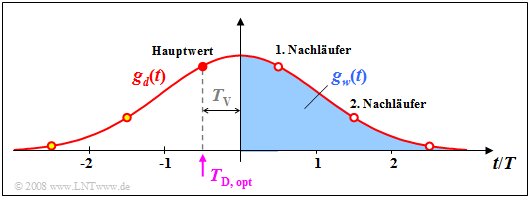
$\text{Definition:}$  Eine  ideale Entscheidungsrückkopplung  liegt vor,  wenn am Entscheider der folgende Grundimpuls anliegt:

$$g_k(t) = \left\{ \begin{array}{c} g_d(t) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} \text{für} \\ \text{für} \\ \end{array} \begin{array}{*{20}c} t < T_{\rm D} + T_{\rm V}, \\ t \ge T_{\rm D} + T_{\rm V}. \\ \end{array}$$

• Das bedeutet,  dass im Idealfall der Kompensationsimpuls  $g_w(t)$  den linear vorentzerrten Impuls  $g_d(t)$  für alle Zeiten  $t > T_{\rm D} + T_{\rm V}$  exakt nachbilden muss.
• Die aus Realisiserungsgründen erforderliche Verzögerungszeit  $T_{\rm V}$  muss kleiner als die Symboldauer  $T$  sein;  im Folgenden gelte stets  $T_{\rm V} = T/2$.

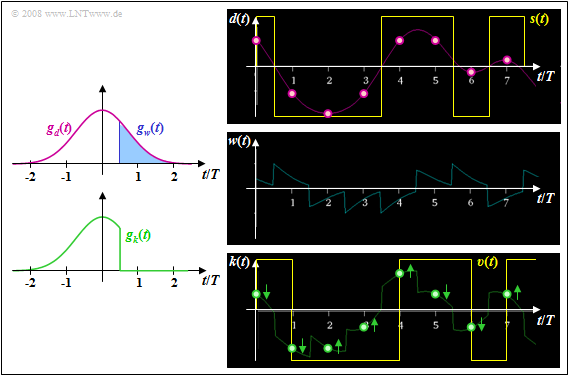
$\text{Beispiel 1:}$  Der Gesamtfrequenzgang  $H_{\rm K}(f) \cdot H_{\rm E}(f) = H_{\rm G}(f)$  sei gaußförmig mit der Grenzfrequenz  $f_{\rm G} = 0.3/T$.  Bei NRZ–Rechteckimpulsen ergibt sich dann der pinkfarben skizzierte Detektionsgrundimpuls  $g_d(t)$.

Grundimpulse und Signale bei idealer  "Decision Feedback Equalization"

⇒   Links dargestellt sind die Grundimpulse  $g_w(t)$  und  $g_k(t)$  bei idealer Entscheidungsrückkopplung,  wobei der Detektionszeitpunkt  $T_{\rm D} = 0$  und die Verzögerungszeit  $T_{\rm V} = T/2$  zugrunde liegen.

⇒   Die rechten Bilder aus  [Söd01] – alle ohne Berücksichtigung des Rauschens – machen deutlich, dass durch die Kompensation aller Impulsnachläufer mittels des Korrektursignals  $w(t)$  die Abstände der Nutzabstandswerte  $d_{\rm S}(\nu \cdot T)$  von der Entscheiderschwelle  $E = 0$  verändert werden.

• Besonders geringe Abstände wie beispielsweise zu den Zeitpunkten  $t = 6T$  und  $t = 7T$  werden deutlich vergrößert und damit deren Fehlerwahrscheinlichkeiten stark verringert  (Pfeile weggehend von der Schwelle).
  

• Dagegen werden die im Signal  $d(t)$  weiter vom Schwellenwert  $E = 0$  entfernten Detektionsabtastwerte zur Schwelle hin verschoben und deren Verfälschungswahrscheinlichkeit somit leicht erhöht.  Dies erkennt man zum Beispiel für den Zeitpunkt  $t = 5T$.

Augenöffnung und Fehlerwahrscheinlichkeit bei DFE

Augendiagramme ohne und mit  "Decision Feedback Equalization"  $(f_{\rm G}\cdot T = 0.3)$

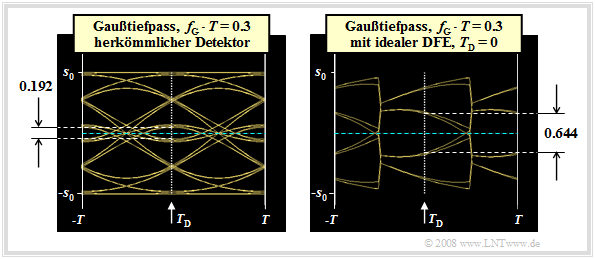
Wir betrachten nun die Augendiagramme

• ohne DFE  (linke Grafik)  und
• mit idealer DFE (rechte Grafik).

Dabei wird von den gleichen Voraussetzungen wie auf der letzten Seite ausgegangen,  so dass folgende Grundimpulswerte vorliegen:

$$g_0 = g_d(t=0) = 0.548 \cdot s_0,$$

$$g_1 = g_d(t=T) = 0.214 \cdot s_0 = g_{-1} \hspace{0.05cm},$$

$$g_2 = g_d(t=2\hspace{0.05cm}T) = 0.012 \cdot s_0 = g_{-2} \hspace{0.05cm},$$

$$g_3 = g_{-3} = \text{...} \approx 0 \hspace{0.05cm}.$$

Die beiden Augendiagramme können wie folgt interpretiert werden:

• Beim herkömmlichen Empfänger (ohne DFE) gilt bei binärer bipolarer redundanzfreier Codierung unter Berücksichtigung der Symmetrie:

$${\ddot{o}(T_{\rm D} = 0 )} = {2} \cdot \big [ g_0 - | g_{-1}| - | g_{-2}| - | g_{1}| - | g_{2}|\big ] = {2} \cdot \big [ g_0 - 2 \cdot g_{1} - 2 \cdot g_{2}\big ]= 0.192 \cdot s_0 \hspace{0.05cm}.$$

• Dagegen werden bei idealer DFE die beiden Nachläufer  $g_1$  und  $g_2$  vollständig kompensiert und man erhält für die vertikale Augenöffnung:

$${\ddot{o}(T_{\rm D} = 0 )} = {2} \cdot \big [ g_0 - | g_{-1}| - |g_{-2}|\big ] = {2} \cdot \big [ g_0 - g_{1} - g_{2}\big ]= 0.644 \cdot s_0 \hspace{0.05cm}.$$

• Da das Korrektursignal  $w(t)$  aus dem entschiedenen und damit rauschfreien Signal  $v(t)$  abgeleitet wird,  wird der Rauscheffektivwert  $\sigma_d$  durch die Entscheidungsrückkopplung nicht verändert.  Der Störabstandsgewinn durch die DFE ist somit im betrachteten Beispiel gleich

$$G_{\rm DFE}= 20 \cdot {\rm lg}\hspace{0.1cm}\frac{0.644}{0.192} \approx 10.5\,{\rm dB} \hspace{0.05cm}.$$

$\text{Fazit:}$  Bei einem Koaxialkabel mit der charakteristischen Kabeldämpfung  $a_\star = 80 \ \rm dB$  und  $10 \cdot \lg \ (E_{\rm B}/N_0) = 80 \ \rm dB$  bedeutet dieser Störabstandsgewinn z.B.,  dass die ungünstigste Fehlerwahrscheinlichkeit  $p_{\rm U}$  durch die DFE von  $7\%$  auf ca.  $4 \cdot 10^{-7}$  verkleinert wird – eine durchaus beachtenswerte Verbesserung.

Optimierung eines Übertragungssystems mit DFE

Die letzte Seite hat bereits deutlich gemacht,  dass die DFE bereits dann einen enormen Störabstandsgewinn bewirkt,  wenn

Augendiagramme mit DFE und optimiertem Detektionszeitpunkt

• von einer festen Grenzfrequenz  $f_{\rm G}$  und
• dem festen Detektionszeitpunkt  $T_{\rm D} = 0$

ausgegangen wird.  Das System lässt sich aber weiter verbessern,  wenn die beiden Parameter  $f_{\rm G}$  und  $T_{\rm D}$  gemeinsam optimiert werden.

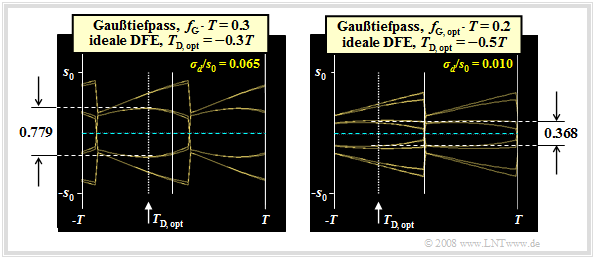
Die Grafik zeigt die Augendiagramme ohne Rauschen für

• $f_{\rm G} \cdot T = 0.3$  (links) und
• $f_{\rm G} \cdot T = 0.2$  (rechts).

Für die Grafik und die nachfolgenden Berechnungen sind weiterhin die charakteristische Kabeldämpfung $a_\star = 80 \ \rm dB$ sowie der AWGN–Parameter $10 \cdot \lg \ (E_{\rm B}/N_0) = 80 \ \rm dB$ (mit $E_{\rm B} = s_0^2 \cdot T$) vorausgesetzt.

Das linke Diagramm ist weitgehend – bis auf den Detektionszeitpunkt $T_{\rm D}$ – identisch mit dem rechten Augendiagramm auf der letzten Seite.

Die Optimierungsergebnisse lassen sich wie folgt zusammenfassen:

• Mit  $f_{\rm G} \cdot T = 0.3$  kann durch Verschiebung des Detektionszeitpunktes auf  $T_\text{D, opt} = -0.3T$  die Augenöffnung auf  $\ddot{o}(T_\text{D, opt}) = 0.779 \cdot s_0$  vergrößert werden.

• Daraus resultiert gegenüber  $T_{\rm D} = 0$  $($vergleiche letze Seite$)$  ein weiterer Störabstandsgewinn von  $G_{T_\text{D, opt}}= 20 \cdot {\rm lg}\hspace{0.1cm}{0.779}/{644} \approx 1.65\,{\rm dB} \hspace{0.05cm}.$

• Die Fehlerwahrscheinlichkeit ergibt sich nun zu  $p_{\rm U} \approx 1.3 \cdot 10^{-9}$  $($gegenüber  $4 \cdot 10^{-7})$.
  

Beim DFE–Empfänger kann man aber zusätzlich die Grenzfrequenz weiter herabsetzen.  Der Grund ist das bessere Rauschverhalten bei kleinerer Grenzfrequenz.  Der normierte Rauscheffektivwert ergibt sich statt zu  $\sigma_d/s_0 = 0.065$  $($für  $f_{\rm G} \cdot T = 0.3)$  zum Beispiel zu  $\sigma_d/s_0 = 0.010$  $($für  $f_{\rm G} \cdot T = 0.2)$.

• So ergibt sich mit  $f_{\rm G} \cdot T = 0.2$  und  $T_{\rm D} = 0$  die zwar kleine,  aber immerhin von Null verschiedene Augenöffnung  $\ddot{o}_{\rm norm} = 0.152$,  die zusammen mit dem sehr günstigen Rauscheffektivwert zum (ungünstigsten) Störabstand  $17.6 \ \rm dB$  und zur (ungünstigsten) Fehlerwahrscheinlichkeit  $p_{\rm U} \approx 1.6 \cdot 10^{-14}$  führt.

• Durch Kombination der Grenzfrequenz  $f_{\rm G} \cdot T = 0.2$  mit dem Detektionszeitpunkt  $T_{\rm D} = -T/2$  erhält man schließlich die bei den getroffenen Voraussetzungen optimale Systemkonfiguration mit der normierten Augenöffnung  $\ddot{o}_{\rm norm} = 0.368$  und dem (ungünstigsten) Störabstand  $10 \cdot \lg \ \rho_{\rm U} = 25.3 \ \rm dB$.

• Die Fehlerwahrscheinlichkeit ist damit (praktisch) Null.  Praxisrelevant ist allerdings diese Konfiguration nicht:   Bereits eine minimale Toleranz der Systemparameter führt schon zu einem geschlossenem Auge.
  

Realisierungsaspekte der Entscheidungsrückkopplung

Als ein wesentliches Ergebnis des letzten Kapitels  "Lineare Nyquistentzerrung"  und des aktuellen Kapitels  "Entscheidungsrückkopplung"  empfiehlt sich folgende Vorgehensweise:

$\text{Fazit:}$  Für ein Übertragungssystem über Kupferleitungen  $($Koaxialkabel,  Zweidrahtleitung$)$  sind aufgrund des erreichbaren Signal–zu–Rauschabstandes am Entscheider folgende Systemvarianten besonders geeignet:

• ein  Mehrstufensystem  $($zum Beispiel  $M = 4)$  und die  optimale Nyquistentzerrung  zur Kompensation der starken Impulsinterferenzen,  hervorgerufen durch die linearen Kanalverzerrungen;
  

• ein  Binärsystem  mit relativ kleiner Bandbreite des Gesamtfrequenzganges  $H_{\rm G}(f) = H_{\rm K}(f) \cdot H_{\rm E}(f)$  und ein nichtlinearer Detektor mit  DFE.

Beide Systemvarianten liefern bei idealisierten Bedingungen vergleichbar gute Resultate.  Zu beachten ist allerdings,  dass es durch Realisierungsungenauigkeiten bei beiden Systemen zu großen Degradationen kommen kann,  die hier am Beispiel des DFE–Systems genannt werden:

• Da über das Fernsprechnetz kein Gleichsignal übertragen werden kann,  für unsere Berechnungen aber  $H_{\rm K}(f=0) = 1$  angenommen wird,  ist am Empfänger eine  "Gleichsignalwiedergewinnung"  erforderlich.  Diese Aussage trifft in gleicher Weise für das quaternäre Nyquistsystem zu.
  

• Beim DFE–System muss der Kompensationsimpuls  $g_w(t)$  den vorentzerrten Grundimpuls  $g_d(t)$  exakt nachbilden.  Dies ist insbesondere dann schwierig,  wenn  $g_d(t)$  sehr breit ist  $($kleine Grenzfrequenz,  zum Beispiel  $f_{\rm G} \cdot T = 0.2)$  und die Optimierung den Detektionszeitpunkt  $T_\text{D, opt} = -T/2$ liefert.
  

• Kommt es aufgrund eines sehr großen Rauschwertes zu einer Fehlentscheidung,  so werden auch die nachfolgenden Symbole mit großer Wahrscheinlichkeit verfälscht.  Allerdings gibt es immer wieder Symbolfolgen,  die diese  "Fehlerfortpflanzung"  unterbrechen.
  

Grundimpulse bei idealer DFE

$\text{Beispiel 2:}$  Die Grafik zeigt den Grundimpuls  $g_d(t)$ 

• für die Grenzfrequenz  $f_{\rm G} \cdot T = 0.2$  (rote Kurve)  und
• den Kompensationsimpuls  $g_w(t)$  für $T_\text{D} = -T/2$  (blau gefüllt).

Hierbei ist eine Verzögerungszeit  $T_\text{V} = -T/2$  zwischen Entscheidung und Beginn der Signalkorrektur berücksichtigt.  Man erkennt:

• Für  $T_\text{D} = -T/2$  ist der erste Nachläufer  $g_d(T_\text{D} +T) = g_d(T/2)$  genau so groß wie der Hauptwert  $g_d(T_\text{D}) = g_d(-T/2)$.

• Gelingt es nicht,  alle Nachläufer vollständig zu kompensieren,  so ergibt sich schnell ein geschlossenes Auge und damit im ungünstigsten Fall  ("Worst–Case")  die Fehlerwahrscheinlichkeit  $p_{\rm U} \approx 50\%$.

Entscheidungsrückkopplung mit Laufzeitfilter

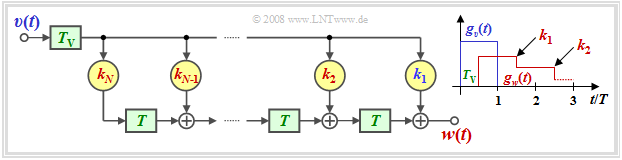
Für eine schaltungstechnische Realisierung genügt es, wenn der korrigierte Grundimpuls  $g_k(t)$  nur zu den äquidistanten Detektionszeitpunkten  $T_\text{D} +\nu \cdot T$  zu Null wird.

Entscheidungsrückkopplung mit Laufzeitfilter

Eine Realisierungsmöglichkeit stellt somit ein unsymmetrisches  Laufzeitfilter  gemäß nebenstehender Grafik dar,

• dessen Ordnung  $N$  (Anzahl der Filterkoeffizienten)  und
  

• dessen Filterkoeffizienten $k_\nu$  $($mit $\nu = 1$, ... , $N)$ 
  
  

durch den Grundimpuls  $g_d(t)$  sowie den Detektionszeitpunkt  $T_\text{D}$  festgelegt sind.

Diese DFE–Realisierung weist folgende Eigenschaften auf:

• Da das Ausgangssignal  $v(t)$  rechteckförmig ist,  ist der Kompensationsimpuls  $g_w(t)$  treppenförmig.
  

• Bei richtiger Dimensionierung der Filterkoeffizienten  $k_\nu$  gilt für  $\nu = 1$, ... , $N$:

$$g_w(T_{\rm D} + \nu \cdot T) = g_d(T_{\rm D} + \nu \cdot T) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} g_k(T_{\rm D} + \nu \cdot T) = 0 \hspace{0.05cm}.$$

• Zum Detektionszeitpunkt  $T_\text{D}$  ergibt sich die genau gleiche vertikale Augenöffnung wie bei idealer DFE.  Nachteilig ist allerdings eine kleinere horizontale Augenöffnung.
  
  

Grundimpulse bei DFE mit Laufzeitfilter

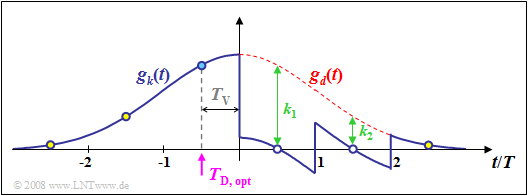
$\text{Beispiel 3:}$  Die Grafik zeigt die Grundimpulse  $g_d(t)$  und  $g_w(t)$  bei der Entscheidungsrückkopplung mit einem Laufzeitfilter zweiter Ordnung.

Es gelten die gleichen Voraussetzungen wie für das  $\text{Beispiel 2}$  auf der letzten Seite:   $f_{\rm G} \cdot T = 0.2$  und  $T_\text{D} = -T/2$.  Man erkennt:

• Wegen der Ordnung  $N = 2$  werden hier allerdings nur die beiden ersten Nachläufer  $g_d(0.5T)$  und  $g_d(1.5T)$  kompensiert.

• Der dritte Nachläufer  $g_d(2.5T)$  könnte durch einen weiteren Filterkoeffizienten  $k_3$  zu Null gemacht werden.

• Dagegen können die Impulsvorläufer  $g_d(-1.5T)$  und  $g_d(-2.5T)$  prinzipiell nicht kompensiert werden.

Aufgaben zum Kapitel

Aufgabe 3.8: Decision Feedback Equalization mit Laufzeitfilter

Aufgabe 3.8Z: Optimaler Detektionszeitpunkt bei DFE