Aufgabe 4.12: Berechnungen zur 16-QAM
Aus LNTwww
Version vom 20. August 2022, 16:33 Uhr von Guenter (Diskussion | Beiträge)
Signalraumkonstellation der $\rm 16–QAM$
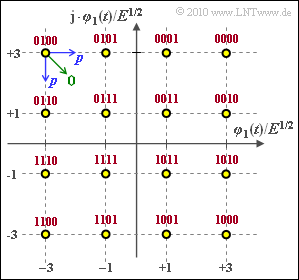
Die Grafik zeigt die Signalraumkonstellation der "Quadraturamplitudenmodulation" mit $M = 16$ Signalraumpunkten.
Für dieses Modulationsverfahren sollen berechnet werden:
- die mittlere Energie pro Symbol bzw. pro Bit,
- die mittlere Symbolfehlerwahrscheinlichkeit $p_{\rm S}$,
- die "Union Bound" $p_{\rm UB}$ als obere Schranke,
- die mittlere Bitfehlerwahrscheinlichkeit $p_{\rm B}$ bei Graycodierung.
Hinweise:
- Die Aufgabe behandelt einen Teilaspekt des Kapitels "Trägerfrequenzsysteme mit kohärenter Demodulation".
- Die Gray–Zuordnung ist in der Grafik angegeben (rote Beschriftung).
- Die Wahrscheinlichkeit, dass das linke obere Symbol in eines der benachbarten Symbole verfälscht wird, wird mit $p$ abgekürzt (blaue Pfeile in der Grafik).
- Eine diagonale Verfälschung ⇒ zwei Bit verfälscht (grüner Pfeil) wird ausgeschlossen.
- Für den AWGN–Kanal gilt mit dem komplementären Gaußschen Fehlerintegral für diese Hilfsgröße: $p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right )\hspace{0.05cm}.$
- Verwenden Sie für numerische Berechnungen $E = 1 \ \rm mWs$ und $p = 0.4\%$.
- Aus diesen Werten kann die AWGN–Rauschleistungsdichte $N_0$ näherungsweise berechnet werden:
- $$p = {\rm Q} \left ( \sqrt{ { 2E}/{ N_0} }\right ) = 0.004 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} { 2E}{ N_0} \approx 2.65^2 \approx 7 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_0 = { E}/{ 3.5}\approx 1.4 \cdot 10^{-4}\,{\rm W/Hz} \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1) Der Quotient $E_{\rm S}/E$ ergibt sich als der mittlere quadratische Abstand der $M = 16$ Signalraumpunkte $\boldsymbol{s}_i$ vom Ursprung.
- Mit der gegebenen Signalraumkonstellation der 16–QAM erhält man:
- $$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} { E}/{ 16} \cdot \left [ 4 \cdot (1^2 + 1^2) + 8 \cdot (1^2 + 3^2) + 4 \cdot (3^2 + 3^2)\right ]={ E}/{ 16} \cdot \left [ 4 \cdot 2 + 8 \cdot 10 + 4 \cdot 18\right ] = 10 \cdot E = \underline{10 \ {\rm mWs}} \hspace{0.05cm}.$$
- Zum gleichen Ergebnis kommt man mit der im Theorieteil angegebenen Gleichung
- $$E_{\rm S} = \frac{ 2 \cdot (M-1)}{ 3 } \cdot E = \frac{ 2 \cdot 15}{ 3 } \cdot E = 10 E \hspace{0.05cm}.$$
(2) Jedes einzelne Symbol stellt vier Binärsymbole dar. Damit ist die mittlere Energie pro Bit.
- $$E_{\rm B} = \frac{ E_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = 2.5 \cdot E = \underline{2.5 \ {\rm mWs}} \hspace{0.05cm}.$$
Zur Verdeutlichung der 16–QAM–Fehlerwahrscheinlichkeit
(3) Die Union Bound ist eine obere Schranke für die Symbolfehlerwahrscheinlichkeit.
- Sie berücksichtigt nur den Übergang zu benachbarten Entscheidungsregionen aufgrund von AWGN–Rauschen.
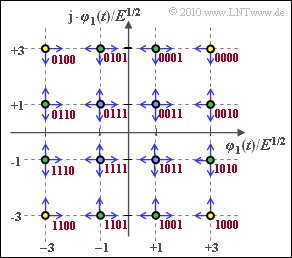
- Aus der Grafik geht hervor, dass die Ecksymbole (gelb gefüllt) nur zu zwei anderen Symbolen hin verfälscht werden können und die restlichen Randsymbole (grüne Füllung) in drei Richtungen.
- Der „worst case” sind die vier inneren Symbole (mit blauer Füllung) mit jeweils vier Verfälschungsmöglichkeiten. Daraus folgt:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) \le 4 \cdot p = \underline{1.6\%}= p_{\rm UB} \hspace{0.05cm}.$$
(4) Zählt man die blauen Pfeile in obiger Grafik, so kommt man auf
- $$4 \cdot 2 + 8 \cdot 3 + 4 \cdot 4 = 48.$$
- Die mittlere Symbolfehlerwahrscheinlichkeit ist somit gleich
- $$p_{\rm S} = { E}/{ 16} \cdot 48 p = 3p = \underline{1.2\%} \hspace{0.05cm}.$$
- Zum gleichen Ergebnis kommt man mit der im Theorieteil angegebenen Gleichung
- $$p_{\rm S} = 4p \cdot \left [ 1 - { 1}/{ \sqrt{M}} \right ] = 4p \cdot \left [ 1 - { 1}/{ 4} \right ] = 3p \hspace{0.05cm}.$$
- Beide Gleichungen gelten nur dann exakt, wenn man wie hier diagonale Verfälschungen ausschließt.
(5) Bei Graycodierung entsprechend der roten Beschriftung in der Grafik bewirkt jeder Symbolfehler genau einen Bitfehler.
- Da aber mit jedem Symbol $M = 4$ Binärsymbole übertragen werden, ist
- $$p_{\rm B} = \frac{ p_{\rm S}}{ {\rm log_2} \hspace{0.05cm}(M)} = \frac{ 1.2\%}{ 4} = \underline{0.3\%} \hspace{0.05cm}.$$
