Eigenschaften von Kupfer–Doppeladern

1. Lineare zeitinvariante Systeme
2. Eigenschaften elektrischer Leitungen
3. Eigenschaften von Kupfer–Doppeladern

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Zugangsnetz eines Telekommunikationssystems

Teilnehmeranschlussbereich bei ISDN

Bei einem Telekommunikationssystem unterscheidet man zwischen

• dem Fern– und Regionalnetz sowie
• dem Teilnehmeranschlussbereich,

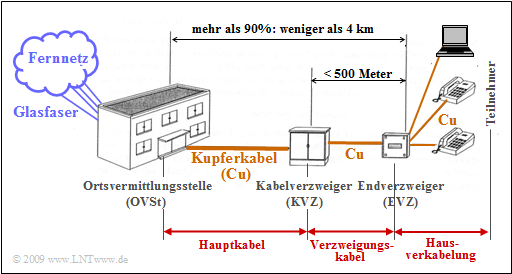
die durch die Ortsvermittlungsstelle voneinander getrennt sind.  Die Grafik zeigt die Netzinfrastruktur bei  $\rm ISDN$  ("Integrated Services Digital Network").

Ursprünglich basierte das gesamte Fernsprechnetz auf Kupferleitungen.  Mitte der 1980–Jahre wurden aber im Weitverkehr die (vorwiegend koaxialen) Kupferkabel durch Glasfaser ersetzt, da der stetig wachsende Bandbreitenbedarf nur mit optischer Übertragungstechnik befriedigt werden konnte.

• Glasfasern im Teilnehmeranschlußbereich sind wegen der immens hohen Verlegekosten bis heute (2009) nicht wirtschaftlich, allerdings gibt es schon lange Planungen zu  "Fiber–to–the–Building"  $\rm (FttB)$  und  "Fiber–to–the–Home"  $\rm (FttH)$ .

• Vielmehr ist man in den letzten zwanzig Jahren den Weg gegangen, durch die Entwicklung und die Verbesserung hochratiger Übertragungssysteme wie  $\rm DSL$  ("Digital Subscriber Line")  über das konventionelle, auf Kupferleitungen basierende Zugangsnetz ausreichend Kapazität bereitzustellen.

$\text{Beispiel 1:}$  In Deutschland ist diese so genannte „Last Mile”   (⇒   der Teilnehmeranschlußbereich)  im Landesdurchschnitt kürzer als vier Kilometer, in städtischen Gebieten zu  $90\%$  sogar kürzer als  $\text{2.8 km}$.  Der Teilnehmeranschlußbereich setzt sich meist wie folgt zusammen:

Bündelung und Verdrillung von Kupferadern

• das  "Hauptkabel"  mit bis zu  $2000$  Doppeladern als Verbindung zwischen Ortsvermittlungsstelle und dem Kabelverzweiger,
• das  "Verzweigungskabel"  zwischen Kabel– und Endverzweiger, mit bis zu  $300$  Doppeladern und deutlich kürzer als ein Hauptkabel  $($maximal  $\text{500 m)}$,
• das  "Hausanschlußkabel"  zwischen Endverzweiger und der Netzabschlußdose beim Teilnehmer mit zwei Doppeladern.

Zur Verminderung des Nebensprechens auf benachbarte Leitungspaare durch induktive und kapazitive Kopplungen und zur Erhöhung der Packungsdichte werden jeweils zwei Doppeladern zu einem so genannten  „Sternvierer”  verseilt.  Die untere Grafik zeigt einen solchen Sternvierer und ein Bündelkabel.

• Hier werden je fünf solcher Vierer zu einem Grundbündel und je fünf Grundbündel zu einem Hauptbündel zusammengefasst.
• Dieses beinhaltet somit  $50$  Doppeladern mit PE–Isolierung  (PE:   Polyethylen).

Dämpfungsmaß von Zweidrahtleitungen

Das Dämpfungsmaß  $α(f)$  und der Wellenwiderstand  $Z_{\rm W}(f)$  von Doppeladern in realen verlegten Kabeln weichen mehr oder weniger stark von der im Kapitel  Einige Ergebnisse der Leitungstheorie  dargelegten Theorie ab. Gründe hierfür sind:

Dämpfungsmaß von Zweidrahtleitungen unterschiedlicher Durchmesser

• Nichtberücksichtigung komplexer Vorgänge der Wirbelstrombildung und der Stromverdrängung,  und
• Inhomogenitäten im Kabelaufbau bei gespleißten Kabelabschnitten.

Verschiedene Netzbetreiber haben  $α(f)$  und  $Z_{\rm W}(f)$  gemessen und daraus empirische Gleichungen abgeleitet.  Wir beziehen uns hier auf die in  [PW95]  dokumentierten Arbeiten von M. Pollakowski und H.W. Wellhausen vom Fernmeldetechnischen Zentralamt der Deutschen Bundespost in Darmstadt.

Diese ermittelten für unterschiedliche Leitungsdurchmesser  $d$  unter anderem das empirische Dämpfungsmaß aus jeweils vierzig Messungen im Frequenzbereich bis  $\text{30 MHz}$  entsprechend der Gleichung

$$\alpha (f) = k_1 + k_2 \cdot (f/{\rm MHz})^{k_3} \hspace{0.05cm}.$$

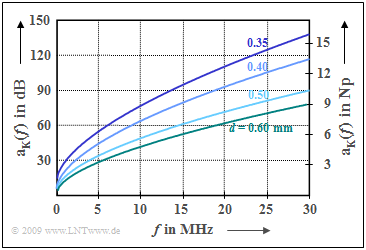
Die Grafik zeigt die Messergebnisse:

• $d = 0.35 \ {\rm mm}$:   $k_1 = 7.9 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 15.1 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.62$,
• $d = 0.40 \ {\rm mm}$:   $k_1 = 5.1 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 14.3 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.59$,
• $d = 0.50 \ {\rm mm}$:   $k_1 = 4.4 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 10.8 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.60$,
• $d = 0.60 \ {\rm mm}$:   $k_1 = 3.8 \ {\rm dB/km}, \hspace{0.2cm}k_2 = \hspace{0.25cm}9.2 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.61$.

Man erkennt aus dieser Darstellung:

• Dämpfungsmaß  $α(f)$  und Dämpfungsfunktion  $a_{\rm K}(f) = α(f) · l$  hängen signifikant vom Leitungsdurchmesser ab. Die seit 1994 verlegten Kabel mit  $d = 0.35 \ \rm (mm)$  und  $d = 0.5$  haben etwa ein um  $10\%$  größeres Dämpfungsmaß als die älteren Leitungen mit  $d = 0.4$  und  $d= 0.6$.
• Dieser mit den Herstellungs– und Verlegungskosten begründete kleinere Durchmesser vermindert allerdings die Reichweite  $l_{\rm max}$  der auf diesen Leitungen eingesetzten Übertragungssysteme signifikant, so dass im schlimmsten Fall teuere Zwischenregeneratoren eingesetzt werden müssen.
• Die heute üblichen Übertragungsverfahren für Kupferleitungen belegen allerdings nur ein relativ schmales Frequenzband, zum Beispiel sind dies bei  $\rm ISDN$  ("Integrated Services Digital Network")   $120\ \rm kHz$  und bei  $\rm DSL$  ("Digital Subscriber Line")  etwa  $1100 \ \rm kHz$.  Für  $f = 1 \ \rm MHz$  beträgt das Dämpfungsmaß für ein 0.4 mm–Kabel etwa  $20 \ \rm dB/km$, so dass selbst bei einer Kabellänge von  $l = 4 \ \rm km$  der Dämpfungswert nicht über  $80 \ \rm dB$  liegt.
• Eine Ausnahme bildet  $\rm VDSL$  ("Very High Data Rate Digital Subscriber Line"), das zum Beispiel die Deutsche Telekom in größeren Städten anbietet.  Hier geht der Frequenzbereich bis  $30 \ \rm MHz$. Deshalb wurden hierfür Glasfaserverbindungen bis zum Kabelverzweiger verlegt, um die noch mit Kupfer zu überbrückende Länge klein zu halten.  Man spricht von "Fibre–to–the–Cabinet"  $\rm (FttC)$.

Umrechnung zwischen $k$– und $\alpha$–Parametern

Zur Berechnung des Frequenzgangs  $H_{\rm K}(f)$  sollte man stets vom gemessenen Dämpfungsmaß

$$\alpha (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}= \alpha_{\rm I} (f) \hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.15cm} f_0 = 1\,{\rm MHz}$$

ausgehen.  Will man dagegen die dazugehörige Zeitfunktion in Form der Impulsantwort  $h_{\rm K}(t)$  ermitteln,  so ist es günstiger, wie im  übernächsten Abschnitt  gezeigt,  wenn das Dämpfungsmaß in der Form dargestellt werden kann,  wie es auch für Koaxialkabel üblich ist:

$$\alpha(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}= \alpha_{\rm II} (f).$$

Als Kriterium dieser Umrechnung benutzen wir,  dass die quadratische Abweichung zwischen beiden Funktionen im Bereich von  $f = 0$  bis  $f = B$  minimal ist:

$$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$

Es ist offensichtlich,  dass  $α_0 = k_1$  gelten wird.  Die Parameter  $α_1$  und  $α_2$  sind von der gewünschten Bandbreite $B$ abhängig.  Sie lauten entsprechend der  Aufgabe 4.6:

$$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot \frac {k_2}{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$

• Für  $k_3 = 1$  (frequenzproportionales Dämpfungsmaß)  ergeben sich folgerichtig die  $\alpha$–Parameter zu

$$\alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} ,$$

• während man für  $k_3 = 0.5$  die folgenden Koeffizienten erhält:

$$\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0}}\hspace{0.05cm}.$$

In diesem Fall steigt das Dämpfungsmaß  $α(f)$  mit der Wurzel aus der Frequenz an.  Es ergibt sich also der gleiche Verlauf wie bei einem Koaxialkabel,  bei dem ja bekanntlich der Skineffekt dominiert.

Nachfolgend wird an drei Beispielen verdeutlicht, wie die zugrundeliegende Bandbreite  $B$  die Ergebnisse dieser Umrechnung beeinflussen.

$\text{Beispiel 2:}$  Bei den folgenden Grafiken gehen wir stets von der Leitungslänge  $l = 1 \ \rm km$  und vom Durchmesser  $d = 0.4 \ \rm mm$  aus,  so dass gilt:

$$k_1 = 5.1 \ \rm dB/km, \ k_2 = 14.3 \ \rm dB/km, \ k_3 = \ 0.59.$$

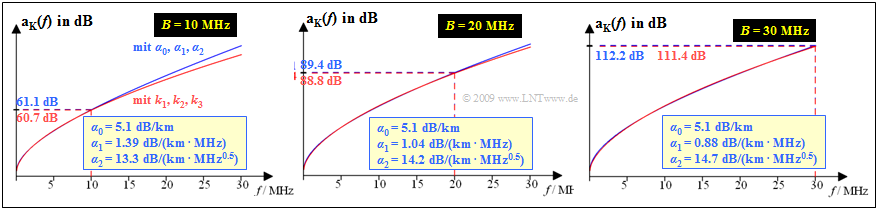
Für diesen Fall zeigt die folgende Grafik

• die mit  $α_0, \ α_1$  und  $α_2$  approximierte Dämpfung (blaue Kurve)
• im Vergleich zum tatsächlichen Verlauf gemäß  $k_1, \ k_2, \ k_3$  (rote Kurve).

Die drei Diagramme gelten für die Bandbreiten  $B = 10 \ \rm MHz$,  $B = 20 \ \rm MHz$  und  $B = \ \rm 30 \ MHz$.

• Die ermittelten Koeffizienten  $α_1$  und  $α_2$  sind angegeben.
• Stets gilt  $α_0 = k_1 = 5.1 \ \rm dB/km$.

Approximation der  $k$–  durch  $\alpha$–Parameter

Man erkennt aus diesen Darstellungen:

• Selbst beim größten Approximationsbereich  $(B = 30 \ \rm MHz)$  nähert die blaue Kurve  $($mit  $α_0,\ α_1,\ α_2)$  den gemessenen Verlauf  $($rote Kurve, beschrieben durch  $k_1, \ k_2, \ k_3)$  sehr gut an.
• Bei kleinerer Bandbreite  $(B = 20 \ \rm MHz$  bzw.  $B = 10 \ \rm MHz)$  ist die Approximation im Bereich  $0≤ f ≤ B$  noch besser,  doch kommt es dann für  $f > B$  zu Verfälschungen.
• Der Dämpfungswert  $a_{\rm K}(f = 30 \ \rm MHz) ≈ 112.2 \ \rm dB$  setzt sich bei der betrachteten Zweidrahtleitung folgendermaßen zusammen:  $4.5\%$  geht auf den Koeffizienten  $α_0$  (Ohmsche Verluste)  zurück,  $23.5\%$  auf den  $f$–proportioanlen Anteil  $α_1$  und  $72\%$  auf den Koeffizienten  $α_2$.
• Das Normalkoaxialkabel  $\text{2.6/9.5 mm}$  weist im Vergleich dazu erst bei einer Länge von  $l = 8.7 \ \rm km$  eine vergleichbare Dämpfung  $(≈ 112 \ \rm dB)$  auf, wobei der Großteil der Dämpfung  $(98.9\%)$ vom Skineffekt  $(α_2)$  herrührt.

In der Gegenrichtung  $(α_1, \ α_2 ⇒ k_2, \ k_3)$  lautet die Umrechnungsvorschrift für den Exponenten:

$$k_3 = \frac{H + 0.5} {H +1}, \hspace{0.8cm}\text{Hilfsgröße: }H = \frac{2} {3} \cdot \frac{\alpha_1 \cdot \sqrt{f_0}}{\alpha_2} \cdot \sqrt{B/f_0}.$$

Mit diesem Ergebnis lässt sich  $k_2$  mit jeder der beiden oben angegebenen Gleichungen berechnen.

Impulsantwort einer Zweidrahtleitung

Mit dieser Koeffizientenumrechnung  $(k_1, \ k_2, \ k_3) \ \ ⇒ \ \ (α_0, \ α_1, \ α_2)$  kann nun für den gesamten Frequenzgang einer Zweidrahtleitung geschrieben werden:

$$H_{\rm K}(f) = H_{\alpha 0}(f) \cdot H_{\alpha 1}(f) \cdot H_{\beta 1}(f)\cdot H_{\alpha 2}(f) \cdot H_{\beta 2}(f) \hspace{0.05cm}.$$

Hierbei sind folgende Abkürzungen verwendet:

$$\begin{align*} H_{\alpha 0}(f) & = {\rm e}^{-\alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l}= {\rm e}^{-{\rm a}_0}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_0= \alpha_0\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l,\\ H_{\alpha 1}(f) & = {\rm e}^{-\alpha_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_1 \cdot 2f/R}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_1 = \alpha_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot {R}/{2} \hspace{0.05cm}, \\ H_{\beta 1}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \beta_1 \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}l} = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.05cm}\tau_{\rm P}} \hspace{0.05cm},\hspace{0.2cm} \tau_{\rm P} = {\beta_1\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l }/({2 \pi}) \hspace{0.05cm}, \\ H_{\alpha 2}(f) & = {\rm e}^{-\alpha_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} {\rm a}_2 = \alpha_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}Np) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm}, \\ H_{\beta 2}(f) & = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}\beta_2 \hspace{0.05cm} \cdot \hspace{0.05cm}\sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm}l}= {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\hspace{0.05cm},\hspace{0.2cm} b_2 = \beta_2\hspace{0.15cm}{\rm (in \hspace{0.15cm}rad) }\cdot l \cdot \sqrt{R/2} \hspace{0.05cm} \end{align*}$$

Auf die Bedeutung der hier implizit definierten Größen wird etwas später eingegangen.

Wir gehen hier zunächst ganz formal vor.  Nach dem  Faltungssatz  gilt für die resultierende Impulsantwort als die  Fourierrücktransformierte  von  $H_{\rm K}(f)$:

$$h_{\rm K}(t) = h_{\alpha 0}(t) \star h_{\alpha 1}(t) \star h_{\beta 1}(t)\star h_{\alpha 2}(t) \star h_{\beta 2}(t) \hspace{0.05cm},$$

$$h_{\alpha 0}(t) \quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad H_{\alpha 0}(f) \hspace{0.05cm},\hspace{0.2cm} h_{\alpha 1}(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad H_{\alpha 1}(f) \hspace{0.05cm},\hspace{0.2cm} {\rm usw.}$$

Diese fünf Anteile sollen nun separat betrachtet werden,  wobei sich die numerischen Ergebnisse auf

• ein digitales Übertragungssystem mit der Bitrate  $R = 30 \ \rm Mbit/s$  und
• eine Zweidrahtleitung mit den Abmessungen  $d = 0.4 \ \rm mm$  und  $l = 1 \ \rm km$ 

beziehen. Damit lauten die  $α$–Koeffizienten in Neper  (Np):

$$\alpha_0 = 0.59\, \frac{ {\rm Np} }{ {\rm km} } \hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.10\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 1.69\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.$$

Das Phasenmaß dieser Leitung ist ebenfalls in  [PW95]  angegeben:

$$b_{\rm K}(f) = \beta_1 \cdot f + \beta_2 \cdot \sqrt {f}\hspace{0.05cm}, \hspace{0.2cm} \beta_1 = 32.9\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 2.26\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$

Als Normierungsgröße der Zeit eignet sich die Symboldauer  $T = 1/R ≈ 33 \ \rm ns$.

Interpretation und Manipulation der einzelnen Impulsantworten

Nun sollen die fünf Impulsantwort–Anteile  $h_{α0}(t), \ h_{α1}(t), \ h_{α2}(t), \ h_{β1}(t)$  und  $h_{β2}(t)$  interpretiert werden:

(1)   Der von den Ohmschen Verlusten herrührende erste Term (frequenzunabhängige Dämpfung) führt zu einer Diracfunktion mit dem Gewicht  $K$,  sodass die Faltung mit  $h_{α0}(t)$  durch die Multiplikation mit  $K = {\rm e}^{–0.59} ≈ 0.55$  ersetzt werden kann:

$$h_{\alpha 0}(t) = K \cdot \delta(t) \hspace{0.25cm}{\rm mit}\hspace{0.25cm} K = {\rm e}^{-{\rm a}_0}\hspace{0.45cm}\Rightarrow\hspace{0.45cm} h_{\rm K}(t) = h_{\alpha 0}(t) \star h_{\rm Rest}(t) = K \cdot h_{\rm Rest}(t)\hspace{0.05cm}.$$

(2)   $H_{α1}(f)$  ist eine reelle und gerade Funktion der Frequenz, so dass auch die Fourierrücktransformierte reell und symmetrisch um  $t =0$  ist:

$$H_{\alpha 1}(f) = {\rm e}^{-2\cdot{\rm a}_1 \cdot |f/R|} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{\alpha 1}(t)= \frac{1}{T} \cdot \frac{{\rm a}_1}{{\rm a}_1^2 + \pi \cdot (t/T)^2}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_1 \hspace{0.15cm}{\rm in \hspace{0.15cm}Np } \hspace{0.05cm}.$$

Mit den beispielhaften Zahlenwerten  $α_1 = 0.1 \ \rm Np/(km · MHz)$,   $l = 1 \ \rm km$,   $R = 30 \ \rm MHz$   ⇒   ${\rm a}_1 = 1.5 \ \rm (Np)$  ergibt sich für das Maximum dieses Anteils:

$$h_{α1}(t = 0) = 1/{\rm a}_1 = 2/3 · 1/T.$$

(3)   Wie bei den Koaxialkabelsystemen führt  $H_{β1}(f)$  zu keiner Signalverzerrung, sondern nur zu einer Zeitverzögerung um die  Phasenlaufzeit:

$$τ_{\rm P} ≈ 5.24 \ \rm µs \hspace{0.2cm} ⇒ \hspace{0.2cm} τ_{\rm P}/T ≈ 157.$$

(4)   Wenden wir uns noch der gemeinsamen Betrachtung der Anteile  $H_{α2}(f)$  und  $H_{β2}(f)$  zu,  die im Zeitbereich durch die Teilimpulsantwort  $h_2(t)$  beschrieben wird:

$$H_{\alpha 2}(f) \cdot H_{\beta 2}(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{2}(t) \hspace{0.05cm}.$$

(5)   Um die Ergebnisse des Kapitels  Eigenschaften von Koaxialkabeln  anwenden zu können,  ersetzen wir  $β_2$  durch  $α_2 · \rm rad/Np$  und  $b_2$  durch  ${\rm a}_2 · \text{rad/Np}$,  so dass  ${\rm a}_2$  und  $b_2$  den gleichen Zahlenwert besitzen. Beispielhaft ersetzt man hier:

$$b_2 = 8.75\, {\rm rad}\hspace{0.2cm} \Rightarrow \hspace{0.2cm} b_2 = 6.55 \,{\rm rad}\hspace{0.05cm}.$$

Man reduziert somit die Konstante  $β_2 = 2.26 \ \rm rad/(km · \sqrt{MHz})$  auf  $β_2 = 1.69 \ \rm rad/(km · \sqrt{MHz})$ .

(6)   Bevor wir den Leser unnötig zu Überlegungen verleiten,  ob diese Näherung tatsächlich zulässig ist oder nicht, geben wir gleich freiwillig zu,  dass diese Annahme die Schwachstelle unserer Überlegungen ist.  Eine Diskussion dieser Fehlannahme folgt im  nächsten Abschnitt.

(7)   Nachdem nun  ${\rm a}_2$  und  $b_2$  die gleichen Zahlenwerte aufweisen,  kann weiter die im Abschnitt  Eigenschaften von Koaxialkabeln  angegebene Gleichung verwendet werden,  wobei  $\rm a_∗$  durch  $\rm a_2$  zu ersetzen ist:

$$h_{\rm 2}(t ) = \frac {1/T \cdot {\rm a_2}}{\pi \cdot \sqrt{2 \cdot(t/T)^3}}\cdot {\rm e}^{ - {{\rm a_2}^2}/( {2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} t/T})} \hspace{0.05cm}, \hspace{0.2cm} {\rm a}_2\hspace{0.15cm}{\rm in \hspace{0.15cm}Np} \hspace{0.05cm}.$$

(8)   Die gesamte Impulsantwort ohne Berücksichtigung der Phasenlaufzeit ergibt sich damit zu

$$h_{\rm K}(t + \tau_{\rm P}) = K \cdot h_{\alpha 1}(t) \star h_{2}(t)\hspace{0.05cm}.$$

Durch Verschiebung um  $τ_{\rm P}$  nach rechts ergibt sich die gesuchte Funktion  $h_{\rm K}(t)$.  Im folgenden Beispiel wird diese Vorgehensweise durch Grafiken verdeutlicht.

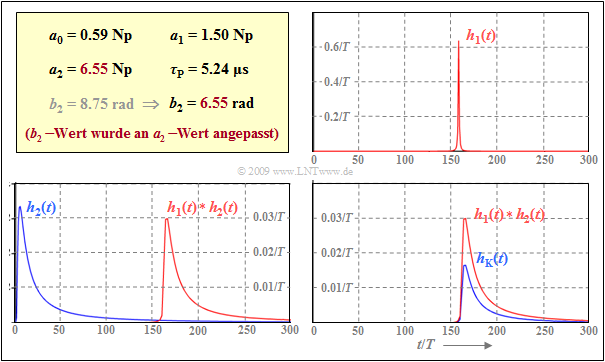
$\text{Beispiel 3:}$  Für die folgenden Grafiken wird weiterhin eine Zweidrahtleitung mit den Abmessungen  $d = 0.4 \ \rm mm$  und  $l = 1 \ \rm km$  vorausgesetzt.  Beachten Sie bitte die unterschiedlichen Ordinatenskalierungen der drei Diagramme in der Grafik.

• Die Bitrate beträgt  $R = 30 \ \rm Mbit/s$   ⇒   Symboldauer  $T ≈ 33\ \rm ns$.
• Wir gehen von den im gelben Kasten angegebenen Größen aus, die auf der letzten Seite berechnet wurden.
• Der  $b_2$–Wert wird dazu von  $8.75 \ \rm rad$  auf  $6.55 \ \rm rad$  verändert und damit an den  ${\rm a}_2$–Wert angepasst.
• Die Auswirkungen dieser Maßnahme werden auf der nächsten Seite interpretiert.

Zur Berechnung der Impulsantwort einer Zweidrahtleitung

Oben rechts ist  $h_1(t) = h_{\rm α1}(t + τ_{\rm P})$  dargestellt.  Dieser Anteil geht auf die Anteile  $α_1$  und  $β_1$  zurück.  $h_1(t)$  ist eine bezüglich der Phasenlaufzeit  $τ_{\rm P}$  symmetrische Funktion mit Maximalwert  $(1.5T)^{–1}$,  wobei der  $1/(1 + t^2$)–Abfall bei  $\pm 5T$  $($rechts und links von  $τ_{\rm P})$ schnell abgeklungen ist.

Das linke untere Diagramm zeigt den Signalanteil  $h_2(t)$,  der auf die beiden Koeffizienten  $α_2$  und  $β_2$  zurückgeht.  $h_2(t)$  ist identisch mit der  Koaxialkabel–Impulsantwort  (ohne Berücksichtigung der Laufzeit),  wenn die charakteristische Kabeldämpfung  $6.55 \ \rm Np$  bzw.  $56.9 \ \rm dB$  beträgt.

Die rote Kurve stellt das Faltungsprodukt  $h_1(t) ∗ h_2(t)$  dar.  Man erkennt, dass die Kurvenform im wesentlichen durch  $h_2(t)$  festliegt.  Die Faltung mit  $h_1(t)$  führt aber neben einem Amplitudenverlust um ca.  $10\%$  auch zu einer (leichten) Verfälschung der Signalform.

Die resultierende Impulsantwort der  $\text{0.4mm}$–Zweidrahtleitung ist im unteren rechten Diagramm als blaue Kurve dargestellt.  Der Unterschied zum rot gezeichneten Faltungsprodukt  $h_1(t) ∗ h_2(t)$  ergibt sich durch den Einfluss der Gleichsignaldämpfung $($Koeffizient  $α_0)$.

Die vorgestellte Methode können Sie sich für beliebige Kenngrößen (Durchmesser, Länge, Bitrate) mit dem SWF–Applet  Zeitverhalten von Kupferkabeln  verdeutlichen.

Diskussion der gefundenen Näherungslösung

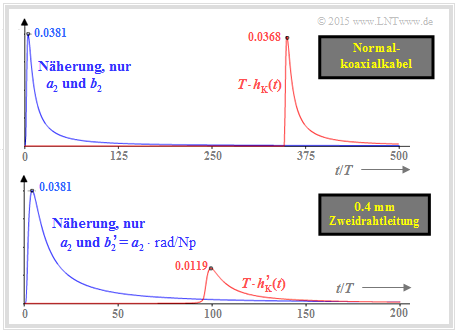
$\text{Beispiel 4:}$  Die folgende Grafik zeigt die (normierten) Impulsantworten  $T · h_{\rm K}(t)$  für zwei beispielhafte Kupferkabel, nämlich

Impulsantwortnäherungen von Normalkoaxialkabeln (oben) und  $\text{0.4 mm}$  Zweidrahtleitung (unten)

• für das  $\text{Normalkoaxialkabel 2.6/9.5 mm}$  bei  $\text{10.1 km}$  Länge (oben), wobei gilt:

$$a_0 = 0.016\,{\rm Np}\hspace{0.05cm}, \hspace{0.15cm} a_1 = 0.020\,{\rm Np}\hspace{0.05cm}, \hspace{0.15cm} a_2 = 6.177\,{\rm Np}\hspace{0.05cm},$$

$$\tau_{ {\rm P} }/T = 350\hspace{0.05cm}, \hspace{0.15cm} b_2 = 6.177\,{\rm rad}\hspace{0.05cm};$$

• für die $\text{0.4 mm Zweidrahtleitung}$ mit der Länge $\text{1.8 km}$ (unten) mit den Kenngrößen

$$a_0 = 1.057\,{\rm Np}\hspace{0.05cm}, \hspace{0.15cm} a_1 = 0.147\,{\rm Np}\hspace{0.05cm}, \hspace{0.15cm} a_2 = 6.177\,{\rm Np}\hspace{0.05cm},$$

$$\tau_{ {\rm P} }/T = 94\hspace{0.05cm}, \hspace{0.15cm} b_2 = 8.260\,{\rm rad}\hspace{0.05cm}.$$

Diese Werte gelten für die Bitrate  $R = 10 \ \rm Mbit/s$   ⇒   Zeitnormierung  $T = 0.1 \ \rm µ s$.

• Die beiden Kabellängen wurden so gewählt, dass sich genau gleiche  $a_2$–Parameter ergeben.
• Für die Zweidrahtleitung wurde der Phasenwert  $b_2 ⇒ b_2\hspace{0.01cm}'$  so angepasst, dass sich wie beim Koaxialkabel für  $b_2\hspace{0.05cm}' = 6.177 \ \rm rad$  und  $a_2 = 6.177 \ \rm Np \ (≈ 53 \ dB)$  gleiche Zahlenwerte ergeben.

Die blauen Kurven zeigen die Näherungen bei Vernachlässigung der  $a_0–,  a_1–$ und  $b_1–$Terme.  Aufgrund der Phasenanpassung  $b_2 ⇒ b_2\hspace{0.01cm}'$  bei der Zweidrahtleitung ergeben sich gleiche Kurvenverläufe.  Das Maximum von ca.  $3.8\%$  liegt bei etwa  $t/T = 4$  (unterschiedlichen Zeitmaßstäbe in beiden Diagrammen!).

Die roten Kurven berücksichtigen auch  $a_0,\ a_1$ und  $b_1$.  Die rote Kurve des Koaxialkabels ist die tatsächliche (normierte) Impulsantwort  $T · h_{\rm K}(t)$.

Aus diesen Darstellungen erkennt man weiter:

• Beim Koaxialkabel können der  $a_0–$Term und der  $a_1–$Term vernachlässigt werden.  Der dadurch entstehende relative Fehler beträgt nur  $3.5\%$.
• Nicht zu vernachlässigen ist dagegen die Phasenlaufzeit  $τ_{\rm P}$, also der  $b_1–$Term.  Beim Koaxialkabel ergibt sich  $τ_{\rm P}/T ≈ 350$, während bei der Zweidrahtleitung  $τ_{\rm P}/T ≈ 94$  gilt  (beachten Sie die unterschiedlichen Zeitmaßstäbe).
• Bei der Zweidrahtleitung (unten) darf man Gleichsignaldämpfung  $(a_0)$  und Querverlust  $(a_1)$  nicht vernachlässigen:  
  Die rote Näherung  $T · h_{\rm K}\hspace{0.01cm}'(t)$  ist um  $70\%$  niedriger als die blaue und zudem etwas breiter.

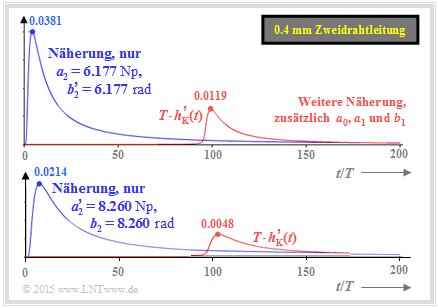
$\text{Beispiel 5:}$  Dieses Beispiel zeigt Näherungen der Impulsantwort einer Zweidrahtleitung  $($Länge $\text{1.8 km}$, Durchmesser $\text{0.4 mm)}$, so dass entsprechend  [PW95]  von folgenden Kenngrößen auszugehen ist:

Zur Impulsantwort einer  $\text{0.4 mm}$  Zweidrahtleitung

$$a_0 = 1.057\,{\rm Np}\hspace{0.05cm}, \hspace{0.15cm} a_1 = 0.147\,{\rm Np}\hspace{0.05cm}, \hspace{0.15cm} a_2 = 6.177\,{\rm Np}\hspace{0.05cm},$$

$$\tau_{ {\rm P} }/T = 94\hspace{0.05cm}, \hspace{0.15cm} b_2 = 8.260\,{\rm rad}\hspace{0.05cm}.$$

Das obere Diagramm – gleich dem unteren Diagramm im  $\text{Beispiel 4}$ – zeigt zwei Näherungen

• bei Vernachlässigung der  $a_0–, \ a_1–$  und  $b_1–$Terme (blaue Kurve),
• bei Berücksichtigung der  $a_0–, \ a_1–$  und  $b_1–$Terme (rote Kurve).

Für dieses obere Diagramm haben wir weiterhin den in [PW95] angegebenen  $a_2–$Koeffizienten übernommen und den genannten Koeffizienten  $b_2 = 8.260 \ \rm rad$  auf  $b_2\hspace{0.01cm}' = 6.177 \ \rm rad$  herabgesetzt.

Anmerkung:   Im Gegensatz zum Koaxialkabel im  $\text{Beispiel 3}$  ist hier wegen  $b_2\hspace{0.01cm}' ≠ b_2$  die rote Kurve  $T · h_{\rm K}\hspace{0.01cm}'(t)$  ebenfalls nur eine Näherung, was in der Grafik durch das Hochkomma vermerkt ist.
Ohne die Korrektur  $b_2\hspace{0.01cm}' = a_2 · \text{rad/Np}$  wäre die  Hilbert–Transformation, die den Zusammenhang zwischen Betrag und Phase bei realen und damit  minimalphasigen Systemen  herstellt, nicht erfüllt. Deshalb ergäbe sich eine akausale Impulsantwort.

Wir glauben deshalb, dass auch bei einer Zweidrahtleitung die beiden Parameter  $a_2$  und  $b_2$  gleiche Zahlenwerte haben müssten.

Wir betrachten nun einen zweiten Ansatz, der im unteren Diagramm dargestellt ist:

• Hier wurde für der in  [PW95]  angegebene Phasenkoeffizient  $b_2 = 8.260 \ \rm rad$  beibehalten.
• Stattdessen wurde der Dämpfungskoeffizient  $a_2 = 6.177 \ \rm Np$  an den Phasenkoeffizienten angepasst (also vergrößert):   $a_2\hspace{0.01cm}' = 8.260 \ \rm Np$.
• Die untere (rote) Impulsantwort   ⇒   ("Worst Case")  ist weniger als halb so hoch und deutlich breiter als die obere Impulsantwort   ⇒   ("Best Case").
• Die tatsächliche (normierte) Impulsantwort  $T \cdot h_{\rm K}\hspace{0.01cm}'(t)$  wird wohl dazwischen liegen. Genauere Aussagen erlauben wir uns nicht.

Nebensprechen auf Zweidrahtleitungen

Bei Übertragungssystemen über Zweidrahtleitungen kann vom gleichen  Blockschaltbild  wie bei den Koaxialkabelsystemen ausgegangen werden, wobei nun

• für den Frequenzgang  $H_{\rm K}(f)$  und die Impulsantwort  $h_{\rm K}(t)$  die in diesem Abschnitt angegebenen Gleichungen zu verwenden sind,
• das weiße Rauschen  $N_0$  nicht mehr die dominante Störungsursache ist,  sondern nun das  Nebensprechen  (englisch:  "Crosstalk")  aufgrund von kapazitiver bzw. induktiver Kopplung benachbarter Doppeladern als stochastische Störung überwiegt.

Durch Verdrillen der Doppeladern eines Sternvierers sowie der Grund– und Hauptbündel entsprechend der Grafik am Ende des Kapitels   Zugangsnetz eines Telekommunikationssystems  wird versucht,  im Mittel eine möglichst symmetrische gegenseitige Kopplung zwischen allen Aderpaaren zu erreichen.  Aufgrund unvermeidbarer Fertigungstoleranzen bleibt aber immer eine leichte Unsymmetrie bestehen.  Diese bewirkt, dass

• an jeden Empfängereingang neben dem „eigenen” Nutzsignal auch  (meist allerdings nur geringe)  Signalanteile von benachbarten Doppeladern gelangen,
• die induzierten Signalanteile für das Nutzsignal eine zusätzliche stochastische Störung darstellen,  die zusammen mit dem thermischen Rauschen das resultierende Störsignal  $n(t)$  ergeben,
• man die Übertragungsqualität nicht oder nur sehr begrenzt durch Erhöhung der Sendeleistung verbessern kann,  da durch diese Maßnahme auch die Nebensprechstörungen größer werden.

Zur Verdeutlichung von Nahnebensprechen (NEXT) und Fernnebensprechen (FEXT)

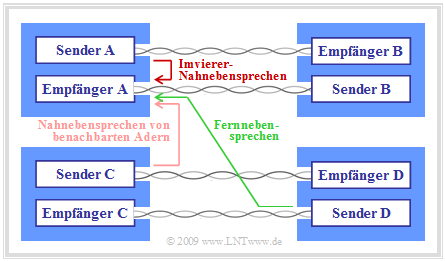
Wie die Grafik verdeutlicht, unterscheidet man zwischen

• Nahnebensprechen  $($"Near–End–Crosstalk"   ⇒   $\rm NEXT)$:
  Der störende Sender speist sein Signal am selben Ende des Kabels ein, an dem der betrachtete Empfänger platziert ist.

• Fernnebensprechen  $($"Far–End–Crosstalk"   ⇒   $\rm NEXT)$:
  Der störende Sender und der gestörte Empfänger befinden sich an entgegengesetzten Kabelenden.

Bei FEXT akkumuliert sich zwar die Störung über die gesamte Kabellänge, wird aber auch durch die Kabeldämpfung stark abgeschwächt. Für gebündelte Kabel im Teilnehmeranschlussbereich ergeben sich somit durch das „Im–Vierer–Nahnebensprechen” um Größenordnungen größerere Störungen als durch das Fernnebensprechen, und auch die Nahnebensprechstörungen von benachbarten Adern können meist vernachlässigt werden.

$\text{Ohne Herleitung:}$  Wir betrachten deshalb im Folgenden ausschließlich das  $\text{Nahnebensprechen (NEXT)}$.  Bei diesem lässt sich das  Leistungsdichtespektrum  (LDS) des Störsignals  $n(t)$  unter Berücksichtigung des unvermeidbaren thermischen Rauschens  $(N_0/2)$  wie folgt darstellen:

$${\it \Phi}_n(f) = {N_0}/{2}+{\it \Phi}_{\rm NEXT}(f) \hspace{0.05cm},\hspace{0.3cm}{\rm mit} \hspace{0.3cm}{\it \Phi}_{\rm NEXT}(f) = {\it \Phi}_{s}(f) \cdot\vert H_{\rm NEXT}(f)\vert ^2 \approx {\it \Phi}_{s}(f) \cdot [K_{\rm NEXT} \cdot f]^{3/2}\hspace{0.05cm}.$$

Zu dieser Gleichung ist anzumerken:

• Die Gleichung ergibt sich durch Integration der lokalen Kopplungen über die gesamte Länge eines kurzen Abschnitts, wobei die Kopplungen zwischen allen Kupferleitungen durch Querkapazitäten und –Induktivitäten modelliert werden.
• ${\it \Phi}_s(f)$  ist das LDS des störenden Senders, woraus sich durch Integration die Sendeleistung  $P_{\rm S}$  ergibt.  Nimmt man an, dass die gestörte Übertragung das gleiche Sendesignal und damit auch das gleiche LDS  ${\it \Phi}_s(f)$  wie der Störer verwendet, so wird deutlich, dass durch eine Erhöhung von  $P_{\rm S}$  lediglich der (relative) Einfluss des thermischen Rauschens  $(N_0/2)$  vermindert wird.
• Der das Nahnebensprechen quantifizierende Faktor  $K_{\rm NEXT}$  hängt stark vom Adernabstand ab, ebenso vom Unsymmetriegrad entlang des Kabels.  Dagegen ist dieser Faktor  $K_{\rm NEXT}$  nahezu unabhängig vom Leiterdurchmesser  $d$  und von der Leitungslänge  $l$.
• Das Produkt  $K_{\rm NEXT} · f$  (dimensionslos) ist im gesamten Betriebsbereich der Leitung, zum Beispiel für alle Frequenzen  $0 ≤ f ≤ 30 \ \rm MHz$, stets sehr viel kleiner als $1$.  Die Nebensprechstörung steigt mit der Frequenz stark $($das heißt mit dem Exponenten $1.5)$ an.
• In  [PW95]  werden nach einer Messreihe über vierzig Doppeladern für die Frequenz  $f = 10 \ \rm MHz$  folgende Werte genannt  $($für  $f = 30 \ \rm MHz$  sind diese Werte noch mit  $3^{3/2} ≈ 5.2$  zu multiplizieren$)$:

• ungünstigster Fall:   $|H_{\rm NEXT}(f = 10 \ \rm MHz)|^2 ≈ 0.001$,
• Mittelung über 40 Adern:   $|H_{\rm NEXT}(f = \ \rm 10 MHz)|^2 ≈ 0.0004$.

• Die Werte gelten für das Im–Vierer–Nahnebensprechen  (störender Sender und gestörter Empfänger im gleichen Sternvierer).
• Nahnebensprechstörungen zwischen weiter entfernten Adern weisen zwar die gleiche Frequenzabhängigkeit auf, sind aber kleiner als das Im–Vierer–Nahnebensprechen:

• Nahnebensprechen zwischen benachbarten Sternvierern um ca.  $5 \ \rm dB$,
• Nahnebensprechen zwischen benachbarten Grundbündeln um ca.  $10 \ \rm dB$,
• Nahnebensprechen zwischen nicht benachbarten Grundbündeln um ca.  $25 \ \rm dB$.

$\text{Fazit:}$ 

• Um solche Nahnebensprechstörungen zu vermeiden oder zumindest zu vermindern, werden benachbarte Doppeladern häufig mit ganz unterschiedlichen Signalen  (analoge Telefonie, ISDN, DSL oder andere breitbandige Dienste)  belegt, die möglichst auch noch unterschiedliche Frequenzbänder benutzen.
• Durch geschickte Auswahl der Doppeladern können nun benachbarte Adern mit Signalen belegt werden, deren Spektren möglichst wenig überlappen, wodurch die Nebensprechstörungen vermindert werden.

Aufgaben zum Kapitel

Aufgabe 4.6: $k$-Parameter und $\alpha$-Parameter

Aufgabe 4.6Z: ISDN-Versorgungsleitungen

Aufgabe 4.7: Kupfer-Doppelader 0.5 mm

Aufgabe 4.8: Nebensprechstörungen