Aufgabe 2.5: Verzerrung und Entzerrung

Trapezspektrum (oben),
zugehörige Impulsantwort (unten)

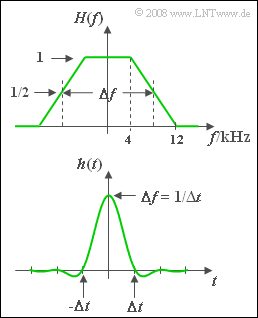
Betrachtet wird ein Nachrichtensystem mit Eingang $x(t)$ und Ausgang $y(t)$, das durch den trapezförmigen Frequenzgang $H(f)$ gemäß der oberen Grafik vollständig beschrieben wird. Mit dem Rolloff–Faktor $r = 0.5$ sowie der äquivalenten Bandbreite $\Delta f = 16 \ \rm kHz$ lautet die dazugehörige, über die Fourierrücktransformation berechenbare Impulsantwort:

$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t ) = \Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot {\rm sinc}(r \cdot \Delta f \cdot t ).$$

Hierbei sind folgende ineinander umrechenbare Funktionen verwendet:

$${\rm si}(x) = \sin(x)/x,\hspace{0.5cm}{\rm sinc}(x) = \sin(\pi x)/(\pi x).$$

Als Eingangssignale stehen zur Verfügung:

Die Summe zweier harmonischer Schwingungen:

$$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot t).$$

Hierbei sei $\omega_1 = 2\pi \cdot 2000 \ {\rm 1/s}$ und $\omega_2 \gt \omega_1$.

Ein periodisches Dreiecksignal:

$$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \big[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}\text{...}\big].$$

Die Grundfrequenz beträgt $f_0 = 2 \ \rm kHz$ bzw. $3\ \rm kHz$. Zum Zeitpunkt $t = 0$ ist der Signalwert in beiden Fällen $1 \ \rm V$.

Ein Rechteckimpuls $x_3(t)$ mit Amplitude $A = 1 \ \rm V$ und Dauer $T = 1 \ \rm ms$.
Da dessen Spektrum $X_3(f)$ bis ins Unendliche reicht, führt $H(f)$ hier immer zu linearen Verzerrungen.

Ab der Teilaufgabe (6) soll versucht werden, durch einen nachgeschalteten Entzerrer mit

Frequenzgang $H_{\rm E}(f)$,
Eingangssignal $y(t)$, und
Ausgangssignal $z(t)$

die eventuell von $H(f)$ erzeugten Verzerrungen zu eliminieren.

Hinweise:

Die Aufgabe gehört zum Kapitel Lineare Verzerrungen.
Bezug wird insbesondere genommen auf die Seite Entzerrungsverfahren.
Der im Fragenkatalog verwendete Begriff „Gesamtverzerrung” bezieht sich auf das Eingangssignal $x(t)$ und das Ausgangssignal $z(t)$.

Fragebogen

Musterlösung

(1) Richtig sind die Lösungsvorschläge 1 und 3:

Durch die Angabe eines Frequenzgangs wird bereits implizit ein lineares System vorausgesetzt, so dass nichtlineare Verzerrungen nicht auftreten können.
Da $H(f)$ rein reell ist, können Phasenverzerrungen ebenfalls ausgeschlossen werden.

(2) Richtig sind die Lösungsvorschläge 1 und 2:

Das Ausgangssignal ist $y_1(t) = x_1(t)$.
Somit ist das System nicht nur verzerrungsfrei, sondern kann für diese Anwendung auch als ideal bezeichnet werden.

(3) Richtig ist der Lösungsvorschlag 3:

In diesem Fall erhält man für das Ausgangssignal:

$$y_1(t)= 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + {1}/{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$

Während der Anteil bei $f_1$ unverändert übertragen wird, ist der Sinusanteil mit $f_2$ auf ein Viertel gedämpft.
Also liegen Dämpfungsverzerrungen vor.

(4) Das Ausgangssignal $y_2(t)$ hat die folgende Form, wenn man die Grundfrequenz $f_0 = 3 \ \rm kHz$ berücksichtigt:

$$y_2(t)= \frac{8\,{\rm V}}{\pi^2} \left( \cos(\omega_0 t) + \frac{3}{8}\cdot \frac{1}{9} \cdot \cos(3\omega_0 t)\right) .$$

Der Faktor $3/8$ beschreibt $H(f = 9 \ \rm kHz)$. Alle weiteren Spektralanteile bei $15 \ \rm kHz$, $21 \ \rm kHz$, usw. werden vom System unterdrückt.

Die stärksten Abweichungen zwischen $x_2(t)$ und $y_2(t)$ wird es bei den Dreieckspitzen geben, da sich hier die fehlenden hohen Frequenzen am stärksten auswirken. Zum Beispiel erhält man für den Zeitpunkt $\underline{t= 0}$:

$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + {3}/{72}\right)= 0.844\,{\rm V} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \varepsilon_{\rm max} = |y_2(t=0)- x_2(t=0)| \hspace{0.15cm}\underline{= 0.156\,{\rm V}}.$$

(5) Mit der Grundfrequenz $f_0 = 2 \ \rm kHz$ sowie den Übertragungswerten $H(3f_0) = 0.75$, $H(5f_0) = 0.25$, $H(7f_0) = 0$ ergibt sich:

$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + \frac{3}{4}\cdot \frac{1}{9} + \frac{1}{4} \cdot\frac{1}{25}\right)= 0.886\,{\rm V}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\varepsilon_{\rm max} \hspace{0.15cm}\underline{= 0.114\,{\rm V}}.$$

(6) Im Bereich bis $4 \ \rm kHz$ ist $H_{\rm E}(f) = H(f) = 1$ zu setzen. Dagegen gilt im Bereich von $4 \ \rm kHz$ bis $12 \ \rm kHz$:

$$H_{\rm E}(f)= \frac{1}{H(f)} = \frac{1}{1.5 \cdot \big[1 - f/(12\,{\rm kHz})\big]} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} H_{\rm E}(f = 10\,{\rm kHz})\hspace{0.15cm}\underline{= 4} .$$

Der Nennerausdruck beschreibt hierbei die Geradengleichung des Flankenabfalls.

(7) Richtig ist der Lösungsvorschlag 1:

Sowohl $x_2(t)$ als auch $x_3(t)$ beinhalten auch Spektralanteile bei Frequenzen größer als $12 \ \rm kHz$.
Wurden diese von $H(f)$ abgeschnitten ⇒ Bandbegrenzung, so können sie durch den Entzerrer nicht mehr rekonstruiert werden.
Das heißt, dass nur das Signal $x_1(t)$ durch $H_{\rm E}(f)$ wieder hergestellt werden kann, allerdings nur dann, wenn $f_2 < 12 \ \rm kHz$ gilt:

$$z_1(t)= \underline{1} \cdot 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + \underline{4} \cdot \frac{1}{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$

Die jeweils ersten (unterstrichenen) Faktoren geben jeweils die Verstärkungswerte von $H_{\rm E}(f)$ an.

	Nichtlineare Verzerrungen.
	Dämpfungsverzerrungen.
	Phasenverzerrungen.

	Es wirkt wie ein ideales System.
	Es wirkt wie ein verzerrungsfreies System.
	Man erkennt, dass ein verzerrendes System vorliegt.

	Beim Signal $x_1(t)$ mit $f_2 = 10 \ \rm kHz$,
	beim Signal $x_2(t)$,
	beim Signal $x_3(t)$.