Rechteckimpuls und zugehöriges Spektrum
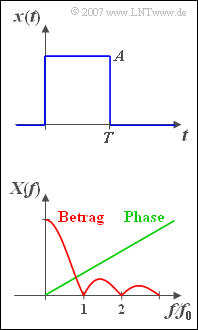
Betrachtet wird ein Rechteckimpuls $x(t)$ der Dauer $T = 50\,\text{µs}$ und der Höhe $A = 2\,\text{V}$. An den Sprungstellen bei $t = 0$ und $t = T$ ist der Signalwert jeweils $A/2$, was aber für die Lösung der Aufgabe keinen Einfluss hat.
In der unteren Grafik ist die dazugehörige Spektralfunktion nach Betrag und Phase qualitativ skizziert. Es gilt:
- $$X( f ) = \left| {X( f )} \right| \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi ( f )} .$$
Der analytische Funktionsverlauf von $X(f)$ soll ermittelt werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Sonderfälle impulsartiger Signale.
- Gegeben sind weiterhin folgende trigonometrischen Umformungen:
- $$\sin ^2( \alpha ) = {1}/{2} \cdot \big( {1 - \cos ( {2\alpha } )} \big),\hspace{0.5cm} \tan( {\alpha /2} ) = \frac{ {1 - \cos ( \alpha )}}{ {\sin ( \alpha )}}.$$
Fragebogen
Musterlösung
(1) Mit der Abkürzung $\omega = 2\pi f$ lautet die Spektralfunktion gemäß dem ersten Fourierintegral:
- $$X( f ) = \int_0^T {A \cdot {\rm{e}}^{-{\rm{j}}\omega t} \hspace{0.05cm}{\rm d}t = } \int_0^T {A \cdot \cos \left( {\omega t} \right)\hspace{0.05cm}{\rm d}t }\hspace{0.1cm}-\hspace{0.1cm} {\rm{j}} \cdot \int_{\rm{0}}^T {A \cdot \sin ( {\omega t} )} \hspace{0.05cm}{\rm d}t.$$
- Nach Integration und Einsetzen der Grenzen folgt daraus:
- $${\mathop{\rm Re}\nolimits} [ {X( f )} ] = \frac{A}{\omega } \cdot \sin( {\omega T} ),$$
- $${\mathop{\rm Im}\nolimits} [ {X( f)} ] = \frac{A}{\omega } \cdot \left( {\cos ( {\omega T}) - 1} \right) = - \frac{A}{\omega } \cdot\left( {1 - \cos ( {\omega T} )} \right).$$
- Für die Frequenz $f = 1/(2T) = 10\, \text{kHz}$ ⇒ $\omega \cdot T = \pi$ erhält man:
- $${\mathop{\rm Re}\nolimits}[{X( {f = 10 \;{\rm{kHz}}} )}] = \frac{A}{ {2{\rm{\pi }}f}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0},$$
- $${\mathop{\rm Im}\nolimits} [ {X( {f = 10 \;{\rm{kHz}}})} ] = \frac{ { - A}}{ {2{\rm{\pi }}f}} \cdot \big( {1 - \cos ( {\rm{\pi }} )} \big) = - \frac{ { A}}{{ {\rm{\pi }}f}}\hspace{0.15 cm}\underline{= - 0.0637 \;{\rm{mV/Hz}}}{\rm{.}}$$
(2) Das Betragsquadrat ist die Summe von Real- und Imaginärteil, jeweils quadriert:
- $$\left| {X( f )} \right|^2 = \frac{ {A^2 }}{ {\omega ^2 }}\big[ {\sin ^2 ( {\omega T} ) + 1 - 2 \cdot \cos ( {\omega T}) + \cos ^2 ( {\omega T} )} \big].$$
- Wegen $\sin^2(\alpha) + \cos^2(\alpha) = 1$ kann hierfür auch geschrieben werden:
- $$\left| {X( f )} \right|^2 = \frac{ {2A^2 }}{ {\omega ^2 }} \cdot \big( {1 - \cos ( {\omega T} )} \big) = \frac{ {4A^2 }}{ {\omega ^2 }} \cdot \sin ^2( {\omega T/2} ).$$
- Setzt man für $\omega = 2\pi f$ und zieht die Wurzel, so erhält man unter der Voraussetzung $A > 0$:
- $$\left| {X( f )} \right| = \left| \frac{A}{ {\rm\pi }f} \cdot \sin ( {\rm \pi }fT ) \right| = A \cdot T \cdot \left| \frac{\sin ( {\rm\pi }fT )}{ {\rm \pi}fT} \right|.$$
- Mit der Abkürzung $\text{si}(x) = \sin(x)/x$ lautet das Ergebnis:
- $$\left| {X( f)} \right| = A \cdot T \cdot\left|{\rm si} ( { {\rm{\pi }}fT} ) \right|.$$
- Der Spektralwert bei der Frequenz $f = 1/T = \text{20 kHz}$ ergibt sich zu
- $$\left| {X( {f = 20\;{\rm{kHz}}} )} \right| = \frac{ {A \cdot T}}{ {\rm{\pi }}} \cdot \sin ( {\rm{\pi }} ) \hspace{0.15 cm}\underline{= 0}.$$
- Bei der Berechnung des Wertes für $f = 0$ erscheint der Quotient $\text{0 durch 0}$. Durch Anwendung der l'Hospitalschen Regel kann der Grenzwert berechnet werden:
- $$\mathop {\lim }\limits_{x \to 0 } \frac{ {\sin \left( x \right)}}{x} = 1.$$
- Daraus folgt:
- $$\left| {X( {f = 0} )} \right| = A \cdot T \hspace{0.15 cm}\underline{= 0.1 \;{\rm{mV/Hz}}}{\rm{.}}$$
- Dieses Ergebnis ist einsichtig, da nach dem ersten Fourierintegral der Spektralwert bei $f = 0$ genau der Fläche unter der Zeitfunktion entspricht.
Betragsspektrum des Rechteckimpulses
(3) Richtig sind die Lösungsvorschläge 1 und 3:
- Entsprechend dem Ergebnis zur Teilaufgabe (2) treten die Nullstellen im Abstand $f_0 = 1/T$ auf.
- Bei $f_0 = 1/(2T) = f = 10 \;{\rm{kHz}}$ ist zwar der Realteil $0$, aber nicht der Imaginärteil.
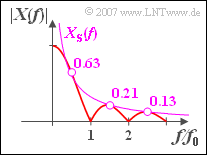
- Bei den Argumenten $f \cdot T = 0.5,\ 1.5,\ 2.5,\hspace{0.05cm}\text{ ... }$ ist die Sinusfunktion jeweils betragsmäßig gleich $1$, und es gilt:
- $$\left| {X( f )} \right| = \frac{A}{ {{\rm{\pi }}\left| f \right|}} = X_{\rm S} ( f ).$$
- Bei anderen Frequenzen dient $X_{\rm S}(f)$ als obere Schranke, das heißt, es gilt stets $|Xf)| \leq X_{\rm S}(f)$.
- In der Skizze ist diese Schranke zusätzlich zu $|X(f)|$ als violette Kurve eingezeichnet.
(4) Nach der Definition auf der Angabenseite kann man die Phasenfunktion wie folgt berechnen:
- $$\varphi ( f ) = - \arctan \frac{ { {\mathop{\rm Im}\nolimits} ( f )}}{ { {\mathop{\rm Re}\nolimits} ( f )}}.$$
- Mit den Ergebnissen aus Teilaufgabe (1) gilt somit:
- $$\varphi ( f ) = \arctan \left( {\frac{ {1 - \cos ( {\omega T} )}}{ {\sin ( {\omega T} )}}} \right).$$
- Das Argument dieser Funktion ist entsprechend der Angabe gleich $\tan(\omega T/2) = \tan(\pi fT)$. Daraus folgt ein mit der Frequenz linear ansteigender Verlauf:
- $$\varphi ( f ) = \arctan \left( {\tan ( { {\rm{\pi }}fT} )} \right) = {\rm{\pi }}fT.$$
- Mit $f = 10\,\text{kHz}$ und $T = 50\,\text{µs}$ erhält man daraus den Phasenwinkel $\pi /2$ entsprechend $\underline{90^{\circ}}$ .
