Aufgabe 4.9Z: Ist bei BPSK die Kanalkapazität C ≡ 1 möglich?
Wir gehen hier von einem binären bipolaren Quellensignal aus ⇒ $ x \in X = \{+1, -1\}$.
Die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$ der Quelle lautet somit:
- $$f_X(x) = {1}/{2} \cdot \delta (x-1) + {1}/{2} \cdot \delta (x+1)\hspace{0.05cm}. $$
Die Transinformation zwischen der Quelle $X$ und der Sinke $Y$ kann gemäß der Gleichung
- $$I(X;Y) = h(Y) - h(N)$$
berechnet werden, wobei gilt:
- $h(Y)$ bezeichnet die differentielle Sinkenentropie
- $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}(f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$
- $${\rm mit}\hspace{0.5cm} f_Y(y) = {1}/{2} \cdot \big[ f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}{X}=-1) + f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}{X}=+1) \big ]\hspace{0.05cm}.$$
- $h(N)$ gibt die differentielle Störentropie an, allein berechenbar aus der WDF $f_N(n)$:
- $$h(N) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}(f_N)} \hspace{-0.35cm} f_N(n) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_N(n) \big] \hspace{0.1cm}{\rm d}n \hspace{0.05cm}.$$
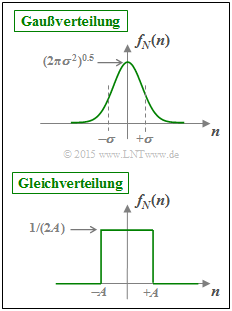
Nimmt man für die Störung $N$ eine Gaußverteilung $f_N(n)$ entsprechend der oberen Skizze an, so ergibt sich die Kanalkapazität $C_\text{BPSK} = I(X;Y)$, die im Theorieteil abhängig von $10 \cdot \lg (E_{\rm B}/{N_0})$ dargestellt ist.
Beantwortet werden soll die Frage, ob es einen endlichen $E_{\rm B}/{N_0}$–Wert gibt, für den $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/Kanalzugriff $ möglich ist ⇒ Teilaufgabe (5).
In den Teilaufgaben (1) bis (4) werden Vorarbeiten zur Beantwortung dieser Frage geleistet. Dabei wird stets von der gleichverteilten Stör–WDF $f_N(n)$ ausgegangen (siehe untere Skizze):
- $$f_N(n) = \left\{ \begin{array}{c} 1/(2A) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.3cm} |\hspace{0.05cm}n\hspace{0.05cm}| < A, \\ {\rm{f\ddot{u}r}} \hspace{0.3cm} |\hspace{0.05cm}n\hspace{0.05cm}| > A. \\ \end{array} $$
Hinweise:
- Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertdiskretem Eingang.
- Bezug genommen wird insbesondere auf die Seite AWGN-Kanalkapazität für binäre Eingangssignale.
Fragebogen
Musterlösung
- $$ h(N) = {\rm log}_2 \hspace{0.1cm} (2A) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: \hspace{0.15cm}h(N) = {\rm log}_2 \hspace{0.1cm} (1/4) \hspace{0.15cm}\underline{= -2\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$
(2) Die Wahrscheinlichkeitsdichtefunktion am Ausgang ergibt sich gemäß der Gleichung:
- $$f_Y(y) = {1}/{2} \cdot \big [ f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}X=-1) + f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}X=+1) \big ]\hspace{0.05cm}.$$
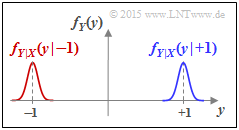
Die Grafik zeigt das Ergebnis für unser Beispiel $(A = 1/8)$:
- Rot gezeichnet ist der erste Term ${1}/{2} \cdot f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}X=-1)$, wobei das Rechteck $f_N(n)$ an die Stelle $y = -1$ verschoben und mit $1/2$ multipliziert wird. Es ergibt sich ein Rechteck der Breite $2A = 1/4$ und der Höhe $1/(4A) = 2$.
- Blau dargestellt ist der zweite Term ${1}/{2} \cdot f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.05cm}|\hspace{0.05cm}X=+1)$ mit der Mitte bei $y = +1$.
- Lässt man die Farben außer Betracht, so ergibt sich die gesamte WDF $f_Y(y)$.
- Die differentiellen Entropie wird nicht verändert wird, wenn man nicht überlappende WDF–Abschnitte verschiebt.
- Somit ergibt sich für die gesuchte differentielle Sinkenentropie:
- $$h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} A=1/8\hspace{-0.05cm}: \hspace{0.15cm}h(Y) = {\rm log}_2 \hspace{0.1cm} (1/2) \hspace{0.15cm}\underline{= -1\,{\rm bit(/Symbol)}}\hspace{0.05cm}.$$
(3) Damit erhält man für die Transinformation zwischen Quelle und Sinke:
- $$I(X; Y) = h(Y) \hspace{-0.05cm}-\hspace{-0.05cm} h(N) = (-1\,{\rm bit/Symbol})\hspace{-0.05cm} -\hspace{-0.05cm}(-2\,{\rm bit/Symbol}) \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$
(4) Alle Lösungsvorschläge sind zutreffend:
- Für jedes $A ≤ 1$ gilt
- $$ h(Y) = {\rm log}_2 \hspace{0.1cm} (4A) = {\rm log}_2 \hspace{0.1cm} (2A) + {\rm log}_2 \hspace{0.1cm} (2)\hspace{0.05cm}, \hspace{0.5cm} h(N) = {\rm log}_2 \hspace{0.1cm} (2A)$$
- $$\Rightarrow \hspace{0.3cm} I(X; Y) = h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(N) = {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm}\underline{= +1\,{\rm bit/Symbol}}\hspace{0.05cm}.$$
- An diesem Prinzip ändert sich auch bei anderer (gleichverteilter) WDF $f_N(n)$ nichts, solange die Störung auf den Bereich $|\hspace{0.05cm}n\hspace{0.05cm}| ≤ 1$ begrenzt ist.
- Überlappen sich jedoch die beiden bedingten Wahrscheinlichkeitsdichtefunktionen, so ergibt sich für $h(Y)$ ein kleinerer Wert als oben berechnet und damit auch eine kleinere Transinformation.
(5) Richtig ist der Lösungsvorschlag 2:
- Die Gaußfunktion klingt zwar sehr schnell ab, sie wird aber nie exakt gleich Null.
- Es kommt immer zu einer Überlappung der bedingten Dichtefunktionen $f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.08cm}|\hspace{0.05cm}X=-1)$ und $f_{Y\hspace{0.05cm}|\hspace{0.05cm}{X}}(y\hspace{0.08cm}|\hspace{0.05cm}X=+1)$.
- Entsprechend der Teilaufgabe (4) ist deshalb $C_\text{BPSK}(E_{\rm B}/{N_0}) ≡ 1 \ \rm bit/Kanalzugriff $ nicht möglich.