Aufgabe 5.5Z: AKF nach Filter 1. Ordnung

• Zurück zum Buch

Nichtrekursives Filter mit zusätzlichem Gleichanteil

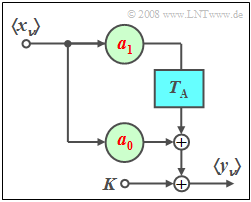
Wir betrachten hier ein nichtrekursives Filter erster Ordnung  $(M = 1)$.

• Die Filterkoeffizienten seien  $a_0 = 0.4$  und  $a_1 = 0.3$.
• Am Filterausgang wird eine Konstante  $K$  hinzuaddiert,  die bis einschließlich Teilaufgabe  (3)  zu Null gesetzt werden soll.

Die einzelnen Elemente der Eingangsfolge  $\left\langle \hspace{0.05cm}{x_\nu } \hspace{0.05cm}\right\rangle$

• sind gaußisch sowie mittelwertfrei,  und
• besitzen jeweils die Streuung  $\sigma_x = 1$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Erzeugung vorgegebener AKF-Eigenschaften.
• Bezug genommen wird auch auf die Kapitel   Autokorrelationsfunktion  $\rm (AKF)$    sowie   Leistungsdichtespektrum  $\rm (LDS)$.

Fragebogen

1

Welche Aussagen sind bezüglich der Ausgangs–AKF zutreffend,  wenn  $K = 0$  gilt?  Begründen Sie Ihre Ergebnisse.

	Der AKF-Wert  $\varphi_y(0)$  gibt die Streuung  $\sigma_y$  an.
	Alle AKF-Werte  $\varphi_y(k \cdot T_{\rm A})$  mit  $|k| \ge 2$  sind Null.
	Das Leistungsdichtespektrum (LDS)  ${\it \Phi}_y(f)$  verläuft cosinusförmig.

2

Berechnen Sie die  AKF–Werte  $\varphi_y(k \cdot T_{\rm A})$  für  $k = 0$  und  $k = 1$.

$\varphi_y(0) \ = \ $

$\varphi_y(T_{\rm A}) \ = $

3

Welche Werte muss man für  $a_0$  und  $a_1$  einstellen,  wenn bei gleicher AKF–Form die Streuung  $\sigma_y = 1$  betragen soll?  Es sei  $a_0 > a_1$.

$a_0 \ = \ $

$a_1 \ = \ $

4

Es gelte  $a_0 = 0.4$  und  $a_1 = 0.3$.  Wie groß ist die Konstante  $K$  zu wählen,  damit sich  $\varphi_y(0)= 0.5$  ergibt?

$K \ = \ $

5

Berechnen Sie mit diesem  $K$–Wert die AKF–Werte für  $k = 1$  und  $k = 2$.

$\varphi_y(T_{\rm A}) \ = \ $

$\varphi_y(2 \cdot T_{\rm A}) \ = \ $

6

Welcher Wert ergibt sich nun für die Streuung  $\sigma_y$?

$\sigma_y \ = \ $

Musterlösung

Musterlösung

(1)  Richtig sind  die Lösungsvorschläge 2 und 3:

• Der AKF–Wert  $\varphi_y(0)$  gibt die Varianz  (Leistung)  $\sigma_y^2$  an und nicht die Streuung  (den Effektivwert)  $\sigma_y$.
• Da ein nichtrekursives Filter erster Ordnung vorliegt,  sind alle AKF–Werte  $\varphi_y(k \cdot T_{\rm A})= 0$  für $|k| \ge 2$.
• Der AKF–Wert  $\varphi_y(- T_{\rm A})$  ist gleich  $\varphi_y(+ T_{\rm A})$.
• Diese beiden AKF-Werte führen zu einer Cosinusfunktion im Leistungsdichtespektrum,  zu der sich noch der Gleichanteil  $\varphi_y(0)$  hinzuaddiert.

(2)  Die allgemeine Gleichung lautet mit  $M = 1$  für  $k \in \{0, \ 1\}$:

$$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k} } .$$

• Daraus erhält man mit  $\sigma_x = 1$:

$$\varphi _y( 0 ) = a_0 ^2 + a_1 ^2 = 0.4^2 + 0.3^2 \hspace{0.15cm}\underline { = 0.25},$$

$$\varphi _y ( { T_{\rm A} } ) = a_0 \cdot a_1 = 0.4 \cdot 0.3 \hspace{0.15cm}\underline {= 0.12}.$$

(3)  Mit den bisherigen Einstellungen ist die Varianz   $\sigma_y^2 = 0.25$   und damit die Streuung  $\sigma_y = 0.5$.

• Durch eine Verdoppelung der Koeffizienten erhält man wie gewünscht  $\sigma_y = 1$:

$$\hspace{0.15cm}\underline {a_0 = 0.8},\quad \hspace{0.15cm}\underline {a_1 = 0.6}.$$

(4)  Die Konstante  $K$  hebt die gesamte AKF um  $K^2$  an.  Mit dem Ergebnis aus  (2)  folgt:

$$K^2 = 0.5 - 0.25 = 0.25\quad \Rightarrow \quad \hspace{0.15cm}\underline {K = 0.5}.$$

(5)  Alle AKF–Werte sind nun um den konstanten Wert  $K^2 = 0.25$  größer.  Somit ist

$$\varphi _y ( { T_{\rm A} } ) = 0.12 + 0.25 \hspace{0.15cm}\underline {= 0.37},$$

$$\varphi _y ( { 2T_{\rm A} } ) = 0 + 0.25 \hspace{0.15cm}\underline {= 0.25}.$$

(6)  Durch die Konstante  $K$  wird die Streuung nicht verändert,  das heißt,  es gilt weiterhin  $\sigma_y = 0.5$. 

• Formal kann diese Größe auch wie folgt berechnet werden:

$$\sigma _y ^2 = \varphi _y ( 0 ) - \mathop {\lim }\limits_{k \to \infty } \varphi _y ( {k \cdot T_{\rm A} } ) = 0.5 - 0.25 = 0.25.$$

• Auch hiermit erhält man wiederum  $\sigma_y \hspace{0.15cm}\underline {= 0.5}$.