Aufgabe 5.6: Filterdimensionierung

• Zurück zum Buch

Gewünschte AKF  $\varphi_y(k \cdot T_{\rm A})$

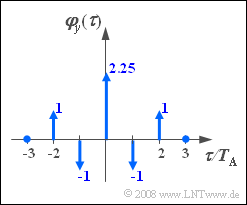
Eine zeitdiskrete Zufallsgröße  $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$  mit der skizzierten Autokorrelationsfunktion  $\rm AKF$  soll mit Hilfe eines digitalen Filters erzeugt werden.

Die zeitdiskreten Gaußschen Eingangswerte  $x_\nu$  seien jeweils gekennzeichnet durch

• den Mittelwert  $m_x = 0$,
• die Streuung  $\sigma_x = 1$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Erzeugung vorgegebener AKF-Eigenschaften.
• Bezug genommen wird auch auf das Kapitel  Autokorrelationsfunktion.
• Alle AKF-Werte  $\varphi_y(k \cdot T_{\rm A})$  mit Index  $|k| \gt 2$  seien Null.

Fragebogen

1

Welche der folgenden Aussagen sind zutreffend?

	Es eignet sich ein rekursives Filter erster Ordnung.
	Es eignet sich ein nichtrekursives Filter erster Ordnung.
	Es eignet sich ein nichtrekursives Filter zweiter Ordnung.
	Die Ausgangswerte  $y_\nu$  sind dreieckverteilt.
	Die Ausgangswerte  $y_\nu$  sind mittelwertfrei  $(m_y = 0)$.

2

Geben Sie die Gleichungen zur Bestimmung der Koeffizienten  $a_0$,  $a_1$  und  $a_2$  an.  Ersetzen Sie die drei Variablen durch  $u = a_1^2$  und  $w = (a_0 + a_2)^2$.
Bestimmen Sie  $u$  und  $w$.  Hinweis:  Es gibt nur eine sinnvolle Lösung.

$u \ = \ $

$w \ = \ $

3

Bestimmen Sie die Filterkoeffizienten  $a_0$,  $a_1$  und  $a_2$.  Geben Sie die folgenden Quotienten ein:

$a_1/a_0 \ = \ $

$a_2/a_0 \ = \ $

4

Wieviele verschiedene Parametersätze  $(I)$  führen zur gewünschten AKF?

$I \ = \ $

Musterlösung

Musterlösung

(1)  Richtig sind  die Lösungsvorschläge 3 und 5:

• Ein rekursives Filter würde stets eine unendlich weit ausgedehnte Impulsantwort  $h(t)$  und damit auch eine unendlich ausgedehnte AKF bewirken.
• Deshalb ist hier eine nichtrekursive Filterstruktur zu wählen.  Die angegebene AKF erfordert die Ordnung  $M= 2$.
• Da die Eingangswerte gaußverteilt und mittelwertfrei sind,  gilt dies auch für die Ausgangswerte.
• Bei der Filterung stochastischer Signale gilt stets:  Gauß bleibt Gauß und Nicht-Gauß wird nie (exakt) Gauß.

(2)  Das Gleichungssystem lautet:

$$k = 2\text{:}\quad a_0 \cdot a_2 = 1.$$

$$k = 1\text{:}\quad a_0 \cdot a_1 + a_1 \cdot a_2 = - 1\quad \Rightarrow \quad \sqrt {u \cdot w} = - 1\quad \Rightarrow \quad u \cdot w = 1.$$

$$k = 0\text{:}\quad a_0 ^2 + a_1 ^2 + a_2 ^2 = 2.25\quad \;\;\, \Rightarrow \quad u + w = 2.25 + 2a_0 \cdot a_2 = 4.25.$$

Das Gleichungssystem bezüglich  $u$  und  $w$  hat zwei Lösungen:

• $u = 4, \ w = 0.25$:   Wegen der Bedingung  $a_2 = 1/a_0$  (siehe erste Gleichung) haben  $a_0$  und  $a_2$  gleiches Vorzeichen.
• Außerdem ist mindestens einer der beiden Koeffizienten größer/gleich  $1$.
• Somit ist die Bedingung  $a_0+a_2= \sqrt{w} = 0.5$  nicht zu erfüllen.
• Die richtige Lösung lautet deshalb  $\underline{u = 0.25}, \ \underline{w = 4}$.

(3)  Das Ergebnis von  (2)  bedeutet,  dass  $a_1 = \pm \sqrt{0.25} = \pm 0.5$  ist.

• Der positive Wert führt zum Gleichungssystem

$$(1) \hspace{0.5cm}0.5 \cdot \left( {a_0 + a_2 } \right) = - 1\quad \Rightarrow \quad a_0 + a_2 = - 2,$$

$$(2) \hspace{0.5cm}a_0 \cdot a_2 = 1.$$

• Daraus folgt  $a_0=a_2=-1$.  Mit  $a_1= 0.5$  erhält man als Endergebnis:

$$a_1/a_0 \hspace{0.15 cm}\underline{= -0.5}, \hspace{0.5 cm} a_2/a_0 \hspace{0.15 cm}\underline{= 1}.$$

• Die Lösung  $a_1= -0.5$  führt zu  $a_0=a_2=+1$  und damit zu den gleichen Quotienten.

(4)  Allgemein hat dieses Problem  $I = 4$  äquivalente Lösungen  $($Spiegelung/Verschiebung sowie jeweils die Multiplikation mit  $-1)$.

• Da hier die Impulsantwort symmetrisch ist,  gibt es allerdings nur  $\underline{I = 2}$  unterschiedliche Lösungen:

$$\text{Lösung 1:} \ \ a_0 = +1,\quad a_1 = - 0.5,\quad a_2 = +1; $$

$$\text{Lösung 2:} \ \ a_0 = - 1,\quad a_1 = +0.5,\quad a_2 = - 1. $$