Aufgabe 5.7Z: Matched-Filter - alles gaußisch

Vorgegebener Gaußimpuls

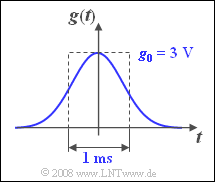
Am Eingang eines Empfangsfilters liegt ein von weißem Rauschen mit der Rauschleistungsdichte $N_0 = 10^{-4}\hspace{0.08cm} \rm V^2 \hspace{-0.1cm}/Hz$ überlagerter Gaußimpuls $g(t)$ mit der Amplitude $g_0$ und der äquivalenten Dauer $\Delta t_g = 1\hspace{0.08cm} \rm ms$ an:

$$g(t) = g_0 \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {t/\Delta t_g } \right)^2 } .$$

Die Impulsenergie beträgt $E_g = 0.01\hspace{0.08cm} \rm V^2 s$. Das Empfangsfilter sei ein akausaler Gaußtiefpass mit dem Frequenzgang

$$H_{\rm E} (f) = {\rm{e}}^{ - {\rm{\pi }}\left( {f/\Delta f_{\rm E} } \right)^2 } .$$

Die dazugehörige Impulsantwort lautet somit:

$$h_{\rm E} (t) = \Delta f_{\rm E} \cdot {\rm{e}}^{ - {\rm{\pi }}\left( {\Delta f_{\rm E} \hspace{0.03cm}\cdot \hspace{0.03cm}t} \right)^2 } .$$

Die systemtheoretische Filterbandbreite $\Delta f_{\rm E}$ soll so gewählt werden, dass der Gaußtiefpass optimal an den Eingangsimpuls $g(t)$ angepasst ist. Man spricht dann von einem Matched-Filter.

Hinweise:

Die Aufgabe gehört zum Kapitel Matched-Filter.

Benutzen Sie zur Lösung das folgende bestimmte Integral:

$$\int_0^\infty {{\rm{e}}^{ - a^2 x^2 } {\rm{d}}x = \frac{{\sqrt {\rm{\pi }} }}{2a}} .$$

Fragebogen

$g_0 \ = \ $

$\ \rm V$

$10 \cdot \lg\ \rho_d(T_\text{D, opt}\hspace{-0.05cm}) \ = \ $

$\ \rm dB$

$\Delta f_\text{E, opt}\ = \ $

$\ \rm kHz$

	Der Nutzabtastwert $d_{\rm S}(T_\text{D, opt}\hspace{-0.05cm})$ ist kleiner als bei Anpassung.
	Die Störleistung $\sigma_d^2$ ist größer als bei Anpassung.
	Das S/N–Verhältnis ist kleiner als in der Teilaufgabe (2) berechnet.

Musterlösung

(1) Für die Energie eines Impulses $g(t)$ gilt allgemein bzw. bei diesem Beispiel:

$$E_g = \int_{ - \infty }^{ + \infty } {g^2(t) \hspace{0.1cm}{\rm{d}}t} = g^2_0 \cdot \int_{ - \infty }^{ + \infty } {{\rm{e}}^{ - 2{\rm{\pi }}\left( {t/\Delta t_g } \right)^2 } \hspace{0.1cm}{\rm{d}}t} .$$

Diese Gleichung kann wie folgt umgeformt werden:

$$E_g = 2 \cdot g_0 ^2 \cdot \int_0^\infty {{\rm{e}}^{ - \left( {\sqrt {2 \rm{\pi }} /\Delta t_g } \right)^2 \cdot \hspace{0.05cm} t^2 }\hspace{0.1cm} {\rm{d}}t} .$$

Mit $a = (2\pi)^{1/2}\cdot 1/\Delta t_g$ und der angegebenen Formel gilt folgender Zusammenhang:

$$E_g = 2 \cdot g_0 ^2 \cdot \frac{{\sqrt {\rm{\pi }} }}{2a} = \sqrt 2 \cdot g_0 ^2 \cdot \Delta t_g .$$

Löst man diese Gleichung nach $g_0$ auf, so erhält man als Endergebnis:

$$g_0 = \sqrt {\frac{E_g }{\Delta t_g \cdot \sqrt 2 }} = \sqrt {\frac{{0.01\;{\rm{V}}^{\rm{2}} {\rm{s}}}}{{0.001\;{\rm{s}} \cdot 1.414}}} \hspace{0.15cm}\underline { = 2.659\;{\rm{V}}}.$$

(2) Unter der Voraussetzung eines Matched–Filters lautet das S/N-Verhältnis am Ausgang:

$$\rho _{d} ( {T_{{\rm{D,}}\,{\rm{opt}}} } ) = \frac{2 \cdot E_g }{N_0 } = \frac{{2 \cdot 10^{ - 2} \;{\rm{V}}^{\rm{2}} {\rm{s}}}}{{10^{ - 4} \;{\rm{V}}^{\rm{2}} {\rm{/Hz}}}} = 200.$$

In logarithmischer Darstellung erhält man folgendes Ergebnis:

$$10 \cdot \lg \rho _{d} ( {T_{{\rm{D,}}\,{\rm{opt}}} } ) = 10 \cdot \lg \left( {200} \right) \hspace{0.15cm}\underline {\approx 23\;{\rm{dB}}}.$$

(3) Ein Vergleich zwischen dem Eingangsimpuls und dem Filterfrequenzgang zeigt, dass bei Anpassung $\Delta f_{\rm E} = 1/\Delta t_g$ gelten muss:

$$\Delta f_{{\rm{E,}}\,{\rm{opt}}} \hspace{0.15cm}\underline { = 1\;{\rm{kHz}}}.$$

(4) Richtig sind die Lösungsvorschläge 1 und 3:

Eine kleinere Filterbandbreite ist günstig bezüglich Störungen,
jedoch ungünstig hinsichtlich des Nutzsignals.
Der negative Einfluss (kleineres Nutzsignal) überwiegt hier gegenüber dem positiven (weniger Störungen).