Aufgabe 5.5: AKF-äquivalente Filter

• Zurück zum Buch

Zwei AKF–äquivalente Filter

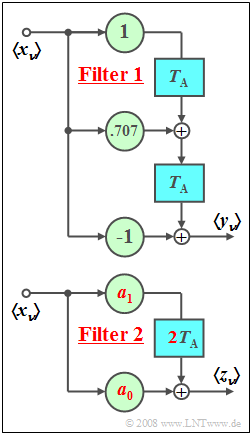
Wir betrachten die beiden skizzierten digitalen Filter:

• Die einzelnen Elemente der Eingangsfolge  $\left\langle {x_\nu } \right\rangle$  sind in beiden Fällen jeweils statistisch voneinander unabhängig und gleichverteilt zwischen  $-1$  und  $+1$.
• Daraus folgt direkt für den Mittelwert und die Varianz:

$$m_x = 0,\quad \sigma _x^2 = {1}/{3}.$$

• Die Verzögerungszeiten von  $\text{Filter 1}$  sind jeweils gleich  $T_{\rm A} = 1 \hspace{0.05cm} \rm µ s$.  Die Verzögerungen von  $\text{Filter 2}$  sind doppelt so lang.

• Die Koeffizienten  $a_0$  und  $a_1$  von  $\text{Filter 2}$  sollen so eingestellt werden,  dass die Autokorrelationsfunktionen  $\rm (AKF)$  von  $\left\langle {y_\nu } \right\rangle$  und von  $\left\langle {z_\nu } \right\rangle$  exakt übereinstimmen.  Wählen Sie bitte bei mehreren Lösungen diejenige mit  $|a_1| < |a_0|$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Erzeugung vorgegebener AKF-Eigenschaften.
• Die Koeffizienten von  $\text{Filter 1}$  werden in den Fragen mit  $\alpha_0$,  $\alpha_1$,  $\alpha_2$  („alphas”) bezeichnet.

Fragebogen

1

Welche Aussagen sind bezüglich  $\text{Filter 1}$  zutreffend?

	Es handelt sich um ein nichtrekursives Filter.
	Die Ordnung des Filters ist  $M = 2$.
	Der obere Filterkoeffizient ist gleich  $\alpha_0 =+1$.

2

Berechnen Sie die Streuung der Ausgangsfolge  $\left\langle {y_\nu } \right\rangle$.

$\sigma_y \ = \ $

3

Berechnen Sie die AKF–Werte  $\varphi_y(k \cdot T_{\rm A})$  für  $k = 1$  und  $k = 2$.

$\varphi_y(T_{\rm A}) \ = \ $

$\varphi_y(2T_{\rm A}) \ = \ $

4

Bestimmen Sie die Koeffizienten von  $\text{Filter 2}$  derart,  dass  $\left\langle {z_\nu } \right\rangle$  und  $\left\langle {y_\nu } \right\rangle$  die gleiche AKF besitzen.  Wie lautet der Quotient  $a_1/a_0$  für  $|a_1| < |a_0|$?

$a_1/a_0 \ = \ $

5

Welche Aussagen treffen für die Wahrscheinlichkeitsdichtefunktionen zu?

	$f_y(y)$  und  $f_z(z)$  sind identisch.
	$f_y(y)$  und  $f_z(z)$  sind im allgemeinen unterschiedlich.
	Bei Gaußscher Eingangsgröße wären  $f_y(y)$  und  $f_z(z)$  gleich.

Musterlösung

Musterlösung

(1)  Richtig sind  die beiden ersten Lösungsvorschläge:

• Es ist ein nichtrekursives Filter zweiter Ordnung mit den Koeffizienten  $\alpha_0 = -1$,  $\alpha_1 = +0.707$  und  $\alpha_2 = +1$.
• Die Koeffizienten von  $\text{Filter 1}$  werden hier mit  $\alpha_0$,  $\alpha_1$,  $\alpha_2$  („alphas”) bezeichnet.

(2)  Die Varianz der Ausgangswerte ist gleich dem AKF–Wert für  $k = 0$.  Für diesen erhält man:

$$\varphi _y (0) = \sigma _x ^2 \cdot \left( {\alpha _0 ^2 + \alpha _1 ^2 + \alpha _2 ^2 } \right) = {1}/{3} \cdot \left( {1 + {1}/{2} + 1} \right) = 0.833.$$

• Damit ergibt sich für die Streuung (bzw. den Effektivwert):

$$\sigma _y = \sqrt {\varphi _y (0)} \hspace{0.15cm} \underline{= 0.913}.$$

(3)  Diese beiden AKF–Werte können wie folgt berechnet werden:

$$\varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _1 + \alpha _1 \cdot \alpha _2 } \right) = {1}/{3} \cdot \left( { - 1 \cdot 0.707 + 0.707 \cdot 1} \right) \hspace{0.15cm} \underline{= 0},$$

$$\varphi _y ( {2T_{\rm A} } ) = \sigma _x ^2 \cdot \left( {\alpha _0 \cdot \alpha _2 } \right) = -1/3\hspace{0.15cm} \underline{\approx - 0.333}.$$

(4)  Wegen  $\varphi _y ( {T_{\rm A} } )= 0$  ist es bei geeigneter Wahl von  $a_0$  und  $a_1$  möglich,  dass die AKF am Ausgang von  $\text{Filter 2}$  identisch ist mit der in  (3)  berechneten AKF.

• Mit  $T_{\rm A}\hspace{0.05cm}' = 2 \cdot T_{\rm A}$  gilt:

$$\varphi _z (0) = {1}/{3} \cdot \left( {a_0 ^2 + a_1 ^2 } \right) = 0.833\quad \Rightarrow \quad a_0 ^2 + a_1 ^2 = 2.5, $$

$$\varphi _z( {T_{\rm A} \hspace{0.05cm}'} ) = {1}/{3}\left( {a_0 \cdot a_1 } \right) = - {1}/{3}\quad \;\;\, \Rightarrow \quad a_0 \cdot a_1 = - 1.$$

• Mit der Hilfsgröße  $H = a_0^2$  führt dies zu der Bestimmungsgleichung

$$H + {1}/{H} = 2.5\quad \Rightarrow \quad H^2 - 2.5 \cdot H + 1 = 0$$

$$\Rightarrow \hspace{0.3cm}H_{1/2} = {1}/{2} \cdot \left( {2.5 \pm \sqrt {2.5^2 - 4} } \right) = {1}/{2} \cdot \left( {2.5 \pm 1.5} \right).$$

• Die beiden Lösungen sind  $H_1 = 2$  und  $H_2 = 1/2$.  Daraus erhält man vier mögliche Lösungen:

$$a_0 = \sqrt 2 ,\quad \;\;\, a_1 = - {1}/{\sqrt 2 }, \hspace{2cm} a_0 = - \sqrt 2 ,\quad a_1 = {1}/{\sqrt 2 },$$

$$a_0 = {1}/{\sqrt 2 },\quad \;\,\, a_1 = - \sqrt 2 , \hspace{2cm} a_0 = - {1}/{\sqrt 2 },\quad a_1 = \sqrt 2 .$$

• Bei den beiden letzten Lösungspaaren ist die Bedingung  $|a_1| < |a_0|$  nicht erfüllt.  Bei den oberen Gleichungen gilt dagegen in beiden Fällen:

$$ \hspace{0.15cm} \underline{a_1 /a_0 = - 0.5}.$$

(5)  Richtig sind die Lösungsvorschläge 2 und 3:

• Im allgemeinen  $($auch bei gleichverteilter Eingangsgröße  $x)$  sind die Dichtefunktionen  $f_y(y)$  und  $f_z(z)$  unterschiedlich.
• $f_z(z)$  ergibt sich in diesem Fall aus der Faltung zweier verschieden breiter Rechtecke; sie ist also trapezförmig.
• Zur Berechnung von  $f_y(y)$  müssten dagegen drei Rechtecke miteinander gefaltet werden.
• Bei Gaußscher Eingangsgröße  $x$  sind auch  $y$  und  $z$  gaußverteilt,  und wegen  $m_y = m_z$  und  $\sigma_y = \sigma_z$  gilt auch  $f_z(z) = f_y(y)$.