Inhaltsverzeichnis
- 1 # ÜBERSICHT ZUM VIERTEN HAUPTKAPITEL #
- 2 Entwicklung der Mobilfunkteilnehmer bis 2010
- 3 Wesentliche Eigenschaften von LTE
- 4 Motivation und Ziele von LTE
- 5 Entwicklung der UMTS-Mobilfunkstandards hin zu LTE
- 6 LTE–Frequenzbandaufteilung
- 7 3GPP – Third Generation Partnership Project
- 8 Aufgabe zum Kapitel
- 9 Quellenverzeichnis
# ÜBERSICHT ZUM VIERTEN HAUPTKAPITEL #
Dieses Kapitel bietet einen Überblick über "Long Term Evolution" $\rm (LTE)$. LTE ist aus heutiger Sicht (2011) ein neuer Mobilfunkstandard, der UMTS ersetzen sollte und vermutlich auch die nächsten Jahre der mobilen Sprach- und Datenübertragung prägen wird.
Im Folgenden wird zunächst eine grobe Übersicht über Motivation, Funktionsweise und Eigenschaften von LTE gegeben. Danach folgt eine tiefer gehende Systembeschreibung der technischen Abläufe bei LTE. Im Einzelnen werden in diesem Kapitel behandelt:
- Die Motivation für LTE und die Frequenzbandaufteilung,
- die Entwicklung der Mobilfunkstandards hin zu LTE,
- einige technische Details zur Sprach– und Datenübertragung,
- das im Uplink genutzte Übertragungsverfahren SC–FDMA und dessen Unterschiede zu OFDMA,
- die Beschreibung und Funktionsweise der verschiedenen Kanäle in der Bitübertragungsschicht,
- ein Ausblick auf das Nachfolgesystem LTE–Advanced.
Nachtrag: Das LTE–Kapitel entstand 2011, also zu der Zeit, als LTE gerade eingeführt wurde. Bei der letzten redaktionellen Überarbeitung im Herbst 2017 wurden einige frühere Aussagen revidiert, die nach sechs Jahren intensiver Nutzung durch viele Kunden nicht mehr den Tatsachen entsprachen. Der Großteil des Kapitels blieb aber gegenüber 2011 unverändert, da sich am LTE–Prinzip in der Zwischenzeit nichts geändert hat.
Entwicklung der Mobilfunkteilnehmer bis 2010
Seit der Jahrtausendwende hat die Anzahl der Mobilanschlüsse drastisch zugenommen.
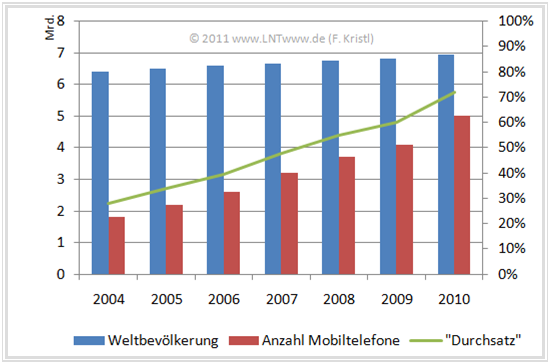
- Die Grafik zeigt für die Jahre 2004 bis 2010 bei den absoluten Zahlen der mobilen Endgeräte (rote Balken, linke Skala) eine Zunahme von $1.8$ auf ca. $5$ Milliarden weltweit.
- Die blauen Balken (linke Skala) geben die Entwicklung der Weltbevölkerung im gleichen Zeitraum an.
- Die (prozentuale) Anzahl der Mobiltelefone (grüne Kurve, rechte Skala) bezogen auf die Weltbevölkerung ist in den Jahren 2004 bis 2010 von knapp $30\%$ auf über $70\%$ gestiegen.
- Dabei fließen Nutzer mit mehr als einem Mobiltelefon in die Statistik ein. 2010 besaßen also keineswegs $70\%$ der Weltbevölkerung ein Mobiltelefon.
- Überproportional zugenommen hat – insbesondere seit der Einführung von Flatrate–Tarifen – die Nutzung mobiler Datendienste.
Die folgenden Aussagen beziehen sich auf das Jahr 2010:
- Der globale mobile Datenverkehr verzeichnete 2010 einen Zuwachs um $159\%$ und ist damit deutlich stärker angestiegen als erwartet.
- Mobile Datenübertragung verursacht seither mehr Netzwerkbelastung als die Sprachübertragung im Mobilfunknetz.
- Allein der mobile Datenverkehr war damit im Vergleichsjahr 2010 dreimal so groß wie das komplette Verkehrsaufkommen 2000 (damals vorwiegend Sprachübertragung).
- Obwohl Smartphones 2010 nur $13\%$ aller mobilen Endgeräte ausmachten, waren sie für $78\%$ der Daten– und Sprachübertragung verantwortlich.
- Zu dieser Entwicklung haben auch $94$ Millionen Laptop–Nutzer beigetragen, die das Internet unterwegs über UMTS–Modems nutzten.
- Ein solcher Laptop–Nutzer verursacht dabei im Mittel die $22$–fache Datenmenge eines durchschnittlichen Smartphone–Benutzers.
Wesentliche Eigenschaften von LTE
Das Kürzel $\rm LTE$ steht für "Long Term Evolution" und bezeichnet den auf UMTS nachfolgenden Mobilfunkstandard. Durch die konzeptionelle Neuentwicklung sollte LTE auf lange Zeit („Long Term”) den sich immer weiter erhöhenden Bedarf an Bandbreite und nach höheren Geschwindigkeiten stillen.
Der LTE–Standard wurde erstmals 2008 als UMTS–Release 8 durch das $\rm 3GGP$ ("Third Generation Partnership Project") – einem Konglomerat verschiedener internationaler Telekommunikationsverbände – definiert und wird seitdem kontinuierlich durch sogenannte „Releases” fortentwickelt. Durch das Bekenntnis der größten Mobilfunkanbieter weltweit ist LTE der erste (großteils) einheitliche Standard der Mobilfunktechnologie.
Man bezeichnet LTE entsprechend der UMTS–Release 8 auch als $\rm 3.9G$, da es die von der ITU ("International Telecommunication Union") spezifizierten Bedingungen für den Mobilfunk der vierten Generation $\rm (4G)$ zunächst nicht ganz erfüllte.
Das nachfolgende Release 10 (vom Juli 2011) genügt dagegen dem 4G–Standard. Im Kapitel LTE–Advanced sind die Features dieser LTE–Weiterentwicklung angegeben. Man bezeichnet diese Technik auch kurz als $\rm LTE–A$.
Nachfolgend sind wichtige Systemeigenschaften von LTE stichpunktartig zusammengestellt, wobei wir uns auf die Seite „ITWissen” berufen:
- LTE basiert auf den Mehrfachzugriffsverfahren $\rm OFDMA$ ("Orthogonal Frequency Division Multiple Access") im Downlink bzw. $\rm SC–FDMA$ ("Single Carrier Frequency Division Multiple Access") im Uplink. Die detaillierte Beschreibung von OFDMA und insbesondere auch dessen Unterschiede zu OFDM findet sich im Kapitel Anwendung von OFDMA und SC–FDMA in LTE.
- Die Verwendung dieses Modulationsverfahrens ermöglicht Orthogonalität zwischen den einzelnen Nutzern, was in einer erhöhten Netzwerkkapazität resultiert [HT09][1]. Diese Technik ermöglicht in Verbindung mit "Multiple Input Multiple Output" $\rm (MIMO)$ derzeit (2011) Spitzendatenraten von $\text{100 Mbit/s}$ im Downlink.
- Neben der gegenüber dem 3G–System UMTS deutlich höheren Datenrate nutzt die LTE–Technik die zur Verfügung stehende Bandbreite effizienter aus. Durch die Kombination dieser Technologie mit den vorhandenen Erfahrungen von GSM und UMTS ist der neue Standard damit nicht nur sehr viel schneller, sondern zudem auch einfacher und flexibler [Mey10][2].
Motivation und Ziele von LTE
Das amerikanische Telekommunikationsunternehmen "Cisco Systems" ging 2010 in einem White Paper davon aus, dass im Jahre 2015
- die Nutzung mobiler Daten um den Faktor $26$ höher sein wird als noch 2010,
- diese Nutzung dabei pro Jahr nochmals um $92\%$ zunimmt, und
- die gigantische Menge von 6.3 Exabyte $(6.3 · 10^{18}$ Byte$)$ pro Monat erreicht wird.
Es wurde außerdem vorausgesagt, dass 2015 fünf Milliarden Menschen mit dem Internet verbunden sein werden [HT09][1]. Darüber hinaus werden aber gleichzeitig weitere kabellose Übertragungstechnologien entwickelt, die ebenso hohe Datenübertragungsraten versprechen. Alle diese Faktoren verlangten nach einer Weiterentwicklung des 3GPP–Mobilfunkstandards „UMTS”.
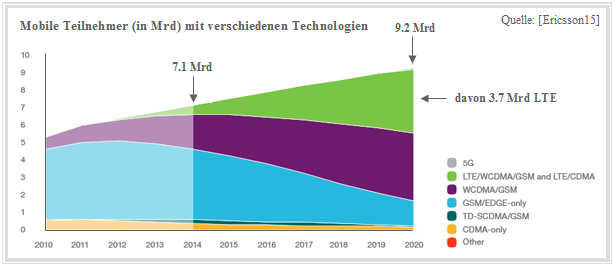
Der Ericsson Mobility Report von 2015 zeigt, dass die Prognose von 2010 übertroffen wurde. 2014 gab es bereits $7.1$ Milliarden mobile Teilnehmer mit Internetzugang, 2020 sollten es $9.2$ Milliarden sein.
Das 3GPP–Konsortium hat früh mit der Definition der LTE–Ziele begonnen, um mit der rasanten Entwicklung bei leitungsbezogenen Verbindungen mithalten zu können.
Die Ziele wurden Ende 2004 in der „LTE Release 6” vergleichend zur HSPA–Technologie ("High–Speed Packet Access") festgeschrieben. Als Hauptziele wurden genannt:
- Eine rein paketorientierte Übertragung und ein hohes Maß an Beweglichkeit und Sicherheit,
- geringere Komplexität, Kostenreduzierung und optimierte Batterielaufzeiten der Endgeräte,
- Bandbreitenflexibilität zwischen $\text{1.5 MHz}$ und $\text{20 MHz}$,
- eine möglichst hohe spektrale Effizienz (Datenrate pro einem Hertz Bandbreite),
- maximal mögliche Datenraten von $\text{100 Mbit/s}$ im Downlink bzw. $\text{50 Mbit/s}$ im Uplink,
- Signaldurchlaufszeiten von weniger als $ 10$ Millisekunden.
Dies bedeutet im Vergleich zu HSPA eine Erhöhung der spektralen Effizienz um den Faktor zwei bis vier, eine Reduktion der Latenz auf die Hälfte und eine Verzehnfachung der maximalen Datenrate. Auf die einzelnen Punkte, die einen Großteil der LTE–spezifischen technischen Charakteristika darstellen, wird im Kapitel Technische Neuerungen von LTE noch genauer eingegangen.
Entwicklung der UMTS-Mobilfunkstandards hin zu LTE
Die Entwicklung der Mobilfunkstandards der dritten Generation wurde bereits im dritten Kapitel dieses Buches ausführlich thematisiert. Aus diesem Grund wird hier nur auf die neueren Entwicklungen detailliert eingegangen.
Zunächst eine kurze unkommentierte Übersicht der UMTS Releases vor LTE aus [Hin08][3]:
- Release 99 (Dezember 1999): UMTS 3G FDD und TDD; $\text{3.84 Mchip/s}$; CDMA–Luftschnittstelle.
- Release 4 (Juli 2001): Niedrigere Chiprate $\text{ (1.28 Mchip/s)}$ bei TDD; einige Korrekturen und kleinere Verbesserungen.
- Release 5 (März 2002): IP Multimedia Subsystem $\rm (IMS)$; High-Speed Downlink Packet Access $\rm (HSDPA)$.
- Release 6 (März 2005): High-Speed Uplink Packet Access $\rm (HSUPA)$; Multimedia Broadcast & Multicast Services $\rm (MBMS)$;
Kooperation mit Wireless LAN; Push–to–Talk; Generic Access Network $\rm (GAN)$.
- Release 7 (Dezember 2007): Verkleinerung der Latenzzeit; verbessertes Quality of Service $\rm (QoS)$; Echtzeitanwendungen $($zum Beispiel $\text{VoIP, EDGE Evolution)}$; $\rm MIMO$ bei UMTS; TDD–Option $\text{7.68 Mchip/s}$.
Das $\text{Release 8}$ vom Dezember 2008 war gleichbedeutend mit der Einführung von "Long Term Evolution" $\rm (LTE)$ und die Basis für die erste Generation von LTE–fähigen Endgeräten. Die wichtigsten Neuerungen und Charakteristiken von Release 8 – zusammengefasst vom 3gpp ("Third Generation Partnership Project") waren:
- Eine hohe spektrale Effizienz und sehr kurze Latenzzeiten,
- die Unterstützung verschiedener Bandbreiten,
- eine einfache Protokoll– und Systemarchitektur,
- Rückwärtskompatibilität und Kompatibilität zu anderen Systemen wie cdma2000,
- $\rm FDD$ ("Frequency Division Duplex") und $\rm FDD$ ("Time Division Duplex") wahlweise nutzbar,
- Unterstützung von "Self-Organizing Networks" $\rm (SON)$.
Auf diese Features (und einige andere mehr) wird im Abschnitt Technische Neuerungen von LTE noch im Detail eingegangen. Das Release 9 enthält demgegenüber nur kleinere Verbesserungen und wird hier nicht näher betrachtet. Das $\text{Release 10}$ vom Juli 2011 beschreibt die Weiterentwicklung LTE–Advanced $\rm (LTE–A)$.
LTE–Frequenzbandaufteilung
Für LTE wurden neue Frequenzen benötigt. In Deutschland gab es 2010 eine Versteigerung zweier Frequenzbereiche, an der sich alle deutschen Mobilfunkbetreiber beteiligten.
Die Grafik veranschaulicht die Ergebnisse dieser Versteigerung der Frequenzen im
- $\text{Bereich um 800 MHz (791 ... 862 MHz)}$:
Hier wurden nur gepaarte Spektren für FDD vergeben: je zweimal $\text{10 MHz}$ für die Telekom, O2 und Vodafone;
- $\text{Bereich um 2.6 GHz (2.5 ... 2.69 GHz)}$:
Vergeben wurden gepaarte Spektren für FDD $(\text{140 MHz})$ und ungepaarte Spektren für TDD $\text{(50 MHz)}$.
Mehr über den Unterschied zwischen FDD und TDD findet man im Abschnitt Motivation für xDSL im Buch „Beispiele von Nachrichtensystemen”.
Die beiden versteigerten Frequenzbereiche haben unterschiedliche Systemeigenschaften, die sie jeweils interessant für verschiedene Anwendungsbereiche machen.
- Der niederfrequentere Bereich $($um $\text{800 MHz)}$ wird auch als „Digitale Dividende” bezeichnet, da er durch die Umstellung der (terrestrischen) TV–Übertragung von PAL auf DVB–T („Digitalisierung”) frei wurde.
- Laut Vereinbarung der Bundesregierung mit den (deutschen) Netzbetreibern muss dieser Bereich dazu genutzt werden, bisher schlecht versorgte Regionen zu „Schnellem Internet” zu verhelfen. Definiert wurden vier Stufen für den Versorgungsgrad einer Region mit Breitbandinternet. Erst wenn in ganz Deutschland $90\%$ der jeweilig vorangegangenen Stufe abgedeckt sein werden, darf mit der nächsten Stufe begonnen werden.
- Die Wahl für dieses Projekt fiel auf den vergleichsweise niedrigen Frequenzbereich um $\text{800 MHz}$ mit besseren Ausbreitungseigenschaften als bei $\text{2600 MHz}$, was für die kostengünstige Versorgung ländlicher Bereiche sinnvoll und auch notwendig ist. Eine LTE–800 Basisstation erreicht einen maximalen Senderadius von etwa $10$ km. Das Verhältnis Nutzer pro Fläche ist aber geringer als bei LTE–2600. Daraus ergibt sich, dass LTE–800 eher für dünn besiedelte Regionen geeignet ist.
- Der Frequenzbereich von $\text{821 MHz}$ bis $\text{832 MHz}$ bleibt frei, um Interferenzen zwischen dem Uplink und dem Downlink zu vermeiden. Man spricht von der „Duplexlücke”. Darüber hinaus kann dieser Frequenzbereich für die Veranstaltungstechnik genutzt werden, da schon vor Einführung von LTE für Funkmikrofone der Frequenzbereich um $\text{800 MHz}$ üblich war. In solchen Gebieten, in denen LTE flächendeckend verfügbar ist, müssen zukünftig Funkmikrofone auf die Duplexlücke ausweichen können.
Die unterschiedliche Bedeutung der Frequenzbereiche aus Betreibersicht werden am Ergebnis der Frequenzversteigerung von 2010 deutlich:
- Die $\text{60 MHz}$ um $\text{800 MHz}$ erbrachten knapp $3.6$ Milliarden Euro $\text{(60 €/Hz)}$, die $\text{190 MHz}$ um $\text{2.6 GHz}$ nur $344$ Millionen Euro $\text{(1,80 €/Hz)}$.
- Zum Vergleich: Die UMTS–Versteigerung im Jahr 2000 ergab die astronomische Summe von $50$ Milliarden Euro für $\text{60 MHz}$ ⇒ $\text{833 €/Hz}$.
3GPP – Third Generation Partnership Project
Auf den letzten Seiten wurde schon mehrfach das "Third Generation Partnership Project" $($oder kurz $\rm 3GPP)$ erwähnt. Hier soll ein kurzer Überblick über das Selbstverständnis dieser Gruppe, seine Struktur und seine Aktivitäten gegeben werden. Die Informationen sind direkt der 3GPP–Website entnommen.
3GPP ist eine Gruppe verschiedener internationaler Normierungsorganisationen, die sich zum Zweck der Vereinheitlichkeit von Mobilfunksystemen zusammengeschlossen haben. Diese wurde am 4.12.1998 von fünf Partnern gegründet:
- $\rm ARIB$ $\rm (A$ssociation of $\rm R$adio $\rm I$ndustries and $\rm B$usinesses, Japan$)$
- $\rm ETSI$ $\rm (E$uropean $\rm T$elecommunication $\rm S$tandards $\rm I$nstitute$)$
- $\rm ATIS$ $\rm (A$lliance for $\rm T$elecommunications $\rm I$ndustry $\rm S$olutions, USA$)$
- $\rm TTA$ $\rm (T$elecommunications $\rm T$echnology $\rm A$ssociation, Korea$)$
- $\rm TTC$ $\rm (T$elecommunications $\rm T$echnology $\rm C$ommittee, Japan$)$
Das 3GPP entwickelt, akzeptiert und pflegt einen weltweit anwendbaren Standard im Mobilfunk. Die regelmäßig und häufig abgehaltenen Konferenzen sind die wichtigsten Instanzen bei der Fortschreibung der Standardisierung der technischen Spezifikationen von LTE.
- Änderungsanträge durchlaufen einen festgesetzten Standardisierungsprozess mit drei Stufen, der hohe Qualität und eine gute Strukturierung der Arbeit des 3GPP ermöglicht.
- Hat ein Release die letzte Stufe erreicht und ist fertiggestellt, wird er von den in den Partnerorganisationen vereinigten Telekommunikationsunternehmen an den Markt weitergegeben.
In [Gut10][4] findet man folgende Einschätzung:
„Ziel der 3GPP–Standardisierung ist die Erstellung technischer Spezifikationen, die alle technischen Details einer Mobilfunktechnologie detailliert beschreiben. Die LTE–Spezifikationen sind extrem umfangreich. Der Detailgrad ist so hoch gewählt, damit Mobilfunkgeräte unterschiedlicher Hersteller in allen Netzen problemlos funktionieren”.
Aufgabe zum Kapitel
A4.1: Allgemeine Fragen zu LTE
Quellenverzeichnis
- ↑ 1,0 1,1 Holma, H.; Toskala, A.: LTE for UMTS – OFDMA and SC–FDMA Based Radio Access. Wiley & Sons, 2009.
- ↑ Meyer, M.: Siebenmeilenfunk. c't 2010, Heft 25, 2010.
- ↑ Hindelang, T.: Mobile Communications. Vorlesungsmanuskript. Lehrstuhl für Nachrichtentechnik, TU München, 2008.
- ↑ Gutt, E.: LTE – eine neue Dimension mobiler Breitbandnutzung. PDF-Dokument im Internet, 2010.