Aufgaben:Aufgabe 1.3: Gemessene Sprungantwort

• Zurück zum Buch

A1.3 Gemessene Sprungantwort

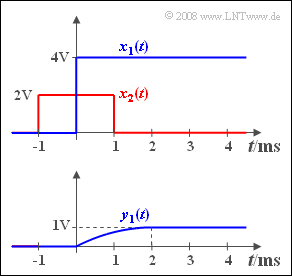
An den Eingang eines linearen zeitinvarianten (LZI–)Übertragungssystems mit Frequenzgang $H(f)$ und Impulsantwort $h(t)$ wird ein sprungförmiges Signal angelegt (blaue Kurve): $$x_1(t) = 4\ {\rm V} \cdot \gamma(t).$$ Das gemessene Ausgangssignal $y_1(t)$ hat dann den in der unteren Grafik dargestellten Verlauf. Mit $T = 2 \,{\rm ms}$ kann dieses Signal im Bereich von $0$ bis $T$ wie folgt beschrieben werden: $$y_1(t) = 2\,{\rm V} \cdot\left[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\right].$$

Ab $t = T $ ist $y_1(t)$ konstant gleich $1 \,{\rm V}$.

In der letzten Teilaufgabe (5) wird nach dem Ausgangssignal $y_2(t)$ gefragt, wenn am Eingang ein symmetrischer Rechteckimpuls $x_2(t)$ der Dauer $T = 2 \ {\rm ms}$ anliegt (siehe roter Kurvenzug in der oberen Grafik).

Hinweise:

• Die Aufgabe gehört zum Kapitel Systembeschreibung im Zeitbereich
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Für den Rechteckimpuls $x_2(t)$ kann mit $A = 2 \ \text{V}$ auch geschrieben werden:

$$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$

• Der Frequenzgang $H(f)$ des hier betrachteten LZI–Systems kann dem Angabenblatt zu Aufgabe 3.8 im Buch „Signaldarstellung” entnommen werden. Allerdings sind die Abszissen– und Ordinatenparameter entsprechend anzupassen.
• Zur Lösung der vorliegenden Aufgabe 1.3 wird $H(f)$ jedoch nicht explizit benötigt.

Fragebogen

1

Welche Aussagen sind anhand der Grafik über das LZI–System möglich?

	$H(f)$ beschreibt ein akausales System.
	$H(f)$ beschreibt ein kausales System.
	$H(f)$ beschreibt einen Tiefpass.
	$H(f)$ beschreibt einen Hochpass.

2

Wie groß ist der Gleichsignalübertragungsfaktor?

$H(f = 0) \ =$

3

Wie lautet die Sprungantwort $σ(t)$? Welcher Wert tritt bei $t = T/2$ auf?

$σ(t = \rm 1 \: ms) \ =$

4

Berechnen Sie die Impulsantwort $h(t)$ des Systems. Welche Werte besitzt diese zu den Zeitpunkten $t = T/2$ und $t = T$?

$h(t = \rm 1 \: ms) \ =$  $\text {1/s}$

$h(t = \rm 2 \: ms) \ =$  $\text {1/s}$

5

Am Eingang liegt der Rechteckimpuls $x_2(t)$ an. Welches Ausgangssignal $y_2(t)$ ergibt sich zu den Zeiten $t = –1\ \text {ms}$, $t = 0$ , $t = +1\ \text {ms}$ und $t = +2\ \text {ms}$?

$y_2(t = \rm \: –1 \: ms) =$  $\text {V}$

$y_2(t = 0) =$  $\text {V}$

$y_2(t = \rm +1 \: ms) =$  $\text {V}$

$y_2(t = \rm +2 \: ms) =$  $\text {V}$

Musterlösung

Musterlösung

(1)  Das Ausgangssignal $y_1(t)$ ist $0$, solange das Eingangssignal $x_1(t) = 0$. Das bedeutet, dass hier ein kausales System vorliegt. Zum gleichen Ergebnis hätte man allein durch die Aussage „das Ausgangssignal wurde gemessen” kommen können. Nur kausale Systeme sind realisierbar und nur bei realisierbaren Systemen kann etwas gemessen werden.

Das Eingangssignal $x_1(t)$ kann für sehr große Zeiten $(t >> 0)$ als Gleichsignal interpretiert werden. Wäre $H(f)$ ein Hochpass, dann müsste $y_1(t)$ für $t → ∞$ gegen 0 gehen. Das heißt: $H(f)$ stellt einen Tiefpass dar. Richtig sind dieLösungsvorschläge 2 und 3..

(2)  Der Gleichsignalübertragungsfaktor kann aus $x_1(t)$ und $y_1(t)$ abgelesen werden, wenn der Einschwingvorgang abgeklungen ist: $$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= \frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$

(3)  Die Sprungantwort $σ(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn am Eingang $x(t) = γ(t)$ anliegen würde. Wegen $x_1(t) = 4 \ \rm {V} · γ(t)$ gilt somit im Bereich von $0$ bis $T = 2 \ \rm ms$: $$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\left( {t}/{T} - 0.5 ({t}/{T})^2\right).$$ Zum Zeitpunkt $t = T = 2 \ \rm ms$ erreicht die Sprungantwort ihren Endwert 0.25. Für $t = T/2 = 1 \ \rm ms$ ergibt sich der Zahlenwert $3/16 \; \underline{\: = \: 0.1875}$. Beachten Sie bitte, dass die Sprungantwort $σ(t)$ ebenso wie die Sprungfunktion $γ(t)$ keine Einheit besitzt.

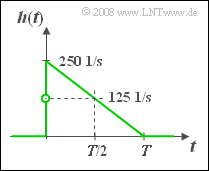
(4)  Die Sprungantwort $σ(t)$ ist das Integral über die Impulsantwort $h(t)$. Damit ergibt sich $h(t)$ aus $σ(t)$ durch Differentiation nach der Zeit. Im Bereich $0 < t < T$ gilt deshalb:

$$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$ $$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$ $$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$ Für $t < 0$ und $t ≥ T$ ist $h(t)$ stets $0$. Der Wert $h(t = 0)$ bei exakt $t = 0$ muss aus dem Mittelwert zwischen links- und rechtsseitigem Grenzwert ermittelt werden: $$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm} 0} h(+ \varepsilon)\right] = \left[ 0 + {0.5}/{T}\right] = {0.25}/{T}= 250 \cdot{1}/{ {\rm s} }.$$

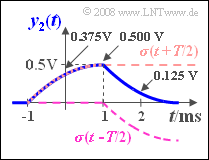
(5)  Der Rechteckimpuls $x_2(t)$ kann auch als die Differenz zweier um $±T/2$ verschobener Sprünge dargestellt werden:

$$x_2(t) = A \cdot \left[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\right].$$ Damit ist das Ausgangssignal gleich der Differenz zweier um $±T/2$ verschobener Sprungantworten: $$y_2(t) = A \cdot \left[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\right].$$ Für $t = \: –T/2 = –1\ \rm ms$ gilt $y_2(t) \;\underline{ = 0}$. Für die weiteren betrachteten Zeitpunkte erhält man wie in der Grafik angegeben: $$y_2(t = 0) = A \cdot \left[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\right] = {\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$ $$y_2(t = T/2) = y_2(t = 1\,{\rm ms}) =A \cdot \left[\sigma( T) - \sigma(0)\right] = {\rm 2\, V}\cdot \left[0.25 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.5\, V}},$$ $$y_2(t = T) = A \cdot \left[\sigma(1.5 \cdot T) - \sigma(0.5 \cdot T)\right] = {\rm 2\, V}\cdot \left[0.25 - 0.1875\right] \hspace{0.15cm}\underline{= {\rm 0.125\, V}}.$$