Stochastische Signaltheorie/Gaußverteilte Zufallsgrößen

1. Stochastische Signaltheorie
2. Kontinuierliche Zufallsgrößen
3. Gaußverteilte Zufallsgrößen

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Allgemeine Beschreibung

Zufallsgrößen mit Gaußscher Wahrscheinlichkeitsdichtefunktion – die Namensgebung geht dabei auf den bedeutenden Mathematiker, Physiker und Astronomen [Friedrich Gauß] zurück – sind wirklichkeitsnahe Modelle für viele physikalische Größen und haben auch für die Nachrichtentechnik eine große Bedeutung. Dies hat mehrere Gründe:

• Nach dem zentralen Grenzwertsatz besitzt jede Linearkombination statistischer Größen

$$x=\sum\limits_{i=\rm 1}^{\it I}x_i ,$$

im Grenzfall $(I → ∞)$ eine Gaußsche WDF, so lange die einzelnen Komponenten keine statistischen Bindungen besitzen. Dies gilt (nahezu) für alle Dichtefunktionen der einzelnen Summanden $x_i$.

• Viele Rauschprozesse erfüllen genau diese Voraussetzung, das heißt, sie setzen sich additiv aus einer sehr großen Anzahl voneinander unabhängiger Einzelbeiträge zusammen, so dass ihre Musterfunktionen (Rauschsignale) eine Gaußsche Amplitudenverteilung aufweisen.
• Legt man ein gaußverteiltes Signal zur spektralen Formung an ein lineares Filter, so ist das Ausgangssignal ebenfalls gaußverteilt. Es ändern sich nur die Verteilungsparameter wie Mittelwert und Streuung sowie die inneren statistischen Bindungen der Abtastwerte.

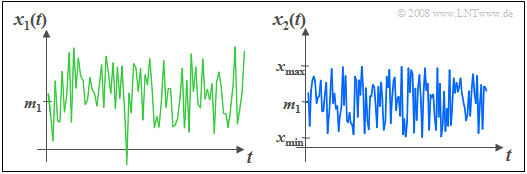
Das Bild zeigt links ein Gaußsches Zufallssignal $x_1(t)$ und rechts im Vergleich dazu ein gleichverteiltes Signal $x_2(t)$ mit gleichem Mittelwert $m_1$ und gleicher Streuung $σ$.

Man erkennt, dass bei der Gaußverteilung im Gegensatz zur Gleichverteilung beliebig große und beliebig kleine Amplitudenwerte auftreten können, auch wenn diese sehr unwahrscheinlich sind im Vergleich zum mittleren Amplitudenbereich.

Wahrscheinlichkeitsdichte- und Verteilungsfunktion

Die Wahrscheinlichkeitsdichtefunktion einer gaußverteilten Zufallsgröße lautet allgemein: $$f_x(x) = \frac{1}{\sqrt{2\pi}\cdot\sigma}\cdot {\rm exp}\left (-\frac{(x-m_1)^2 }{2\sigma^2} \right ).$$ Die Parameter einer Gaußschen WDF sind

• der Mittelwert bzw. der Gleichanteil $m_1$,
• die Streuung bzw. der Effektivwert $σ$.

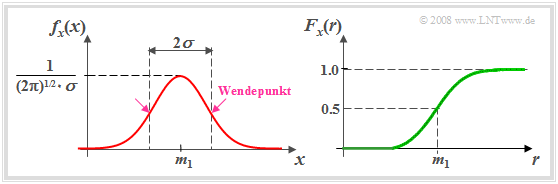
Aus der linken Darstellung geht hervor, dass die Streuung $σ$ als der Abstand von Maximalwert und Wendepunkt aus der glockenförmigen WDF $f_{\rm x}(x)$ auch grafisch ermittelt werden kann. Ist $m_1 =$ 0 und $σ =$ 1, so spricht man oft auch von der Normalverteilung.

Rechts ist die Verteilungsfunktion $F_{\rm x}(r)$ einer gaußverteilten Zufallsgröße dargestellt. Die VTF ist punktsymmetrisch um den Mittelwert $m_1$. Durch Integration über die Gaußsche WDF erhält man: $$F_x(r)= \phi(\frac{\it r-m_{\rm 1}}{\sigma})\hspace{0.5cm}\rm mit\hspace{0.5cm}\rm \phi (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\it \pi}}\int_{-\rm\infty}^{\it x} \rm e^{\it -u^{\rm 2}/\rm 2}\,\, d \it u.$$

Man bezeichnet $ϕ(x)$ als das Gaußsche Fehlerintegral. Dessen Funktionsverlauf ist analytisch nicht berechenbar und muss deshalb aus Tabellen entnommen werden. $ϕ(x)$ lässt sich durch eine Taylorreihe annähern oder aus der in Programmbibliotheken oft vorhandenen Funktion „erf( $x$)” berechnen.

Weitere Informationen zu den gaußverteilten Zufallsgrößen liefert das folgende Lernvideo: Der AWGN–Kanal – Teil 2

Überschreitungswahrscheinlichkeit

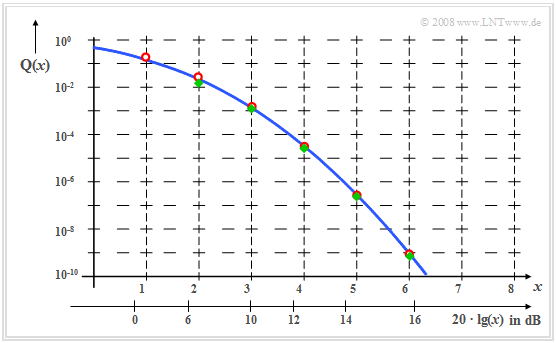
Bei der Untersuchung digitaler Übertragungssysteme muss oft die Wahrscheinlichkeit bestimmt werden, dass eine (mittelwertfreie) gaußverteilte Zufallsgröße $x$ mit der Varianz $σ^2$ einen vorgegebenen Wert $x_0$ überschreitet. Für diese Wahrscheinlichkeit gilt: $$\rm Pr(\it x > x_{\rm 0})=\rm Q({\it x_{\rm 0}}/{\sigma}).$$ Hierbei bezeichnet $Q(x) = 1 − ϕ(x)$ die Komplementärfunktion zu $ϕ(x)$; man nennt diese Funktion das Komplementäre Gaußsche Fehlerintegral und es gilt folgende Berechnungsvorschrift: $$\rm Q (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{\rm +\infty}\hspace{-0.2cm}\rm e^{\it -u^{\rm 2}/\hspace{0.05cm} \rm 2}\,d \it u = \rm 1- \phi (\it x).$$ Dieses Integral ist ebenfalls nicht analytisch lösbar und muss aus Tabellen entnommen werden. In Bibliotheken findet man oft die Funktion „erfc( $x$)”, die mit $Q(x)$ wie folgt zusammenhängt: $$\rm Q(\it x\rm )={\rm 1}/\hspace{0.05cm}{\rm 2}\cdot \rm erfc({\it x}/{\sqrt{\rm 2}}).$$ Speziell für größere $x$–Werte von (also für kleine Fehlerwahrscheinlichkeiten) liefern die nachfolgend angegebenen Schranken eine brauchbare Abschätzung für das Komplementäre Gaußsche Fehlerintegral. $Q_o(x)$ bezeichnet hierbei eine obere und $Q_u(x)$ eine untere Schranke: $$\rm Q_o(\it x \rm )=\frac{\rm 1}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-\it x^{\rm 2}/\hspace{0.05cm}\rm 2}, \hspace{1cm} \rm Q_u(\it x \rm )=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-\it x^{\rm 2}/\hspace{0.05cm}\rm 2} =\rm Q_0(\it x \rm )\left(\rm 1-{\rm 1}/{\it x^{\rm 2}}\right) .$$ Das Grafik zeigt die Q-Funktion in logarithmischer Darstellung für lineare (obere Achse) und logarithmische Abszissenwerte (untere Achse). Die obere Schranke (rote Kreise) ist ab ca. $x =$ 1 brauchbar, die untere Schranke (grüne Rauten) ab $x ≈$ 2. Für $x$-Werte ≥ 4 sind beide Schranken innerhalb der Zeichengenauigkeit vom tatsächlichen Verlauf Q( $x$) nicht mehr zu unterscheiden.

Zentralmomente und Momente

Die Kenngrößen der Gaußverteilung weisen folgende Eigenschaften auf:

• Die Zentralmomente $\mu_k$ (identisch mit den Momenten $m_k$ der äquivalenten mittelwertfreien Zufallsgröße $x – m_1$) sind bei der Gaußschen WDF wie auch bei der Gleichverteilung aufgrund der symmetrischen Verhältnisse für ungerade Werte von $k$ identisch 0. Das Zentralmoment $\mu_2$ ist definitionsgemäß gleich $σ^2$.
• Alle höheren Zentralmomente mit geradzahligen Werten von $k$ lassen sich bei gaußförmiger WDF – wohlgemerkt: ausschließlich bei dieser – durch die Varianz $σ^2$ ausdrücken:

$$\mu_{k}=(k-\rm 1)\cdot (k-\rm 3)\cdot ... \cdot \rm 3\cdot\rm 1\cdot\sigma^k\hspace{0.2cm}\rm (falls\hspace{0.1cm}\it k\hspace{0.1cm}\rm gerade).$$

• Daraus können die nichtzentrierten Momente $m_k$ wie folgt bestimmt werden:

$$m_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot \mu_\kappa \cdot {m_1}^{k-\kappa}.$$

Es ist anzumerken, dass diese Gleichung allgemein gilt, also für beliebige Verteilungen.

• Aus der oberen Gleichung folgt direkt $\mu_4 = 3σ^4$ und daraus für die Kurtosis der Wert $K =$ 3. Den Wert $K$ − 3 bezeichnet man deshalb auch häufig als die Gaußabweichung. Ist diese negativ, so erfolgt der WDF-Abfall schneller als bei der Gaußverteilung. Beispielsweise hat bei einer Gleichverteilung die Gaußabweichung stets den Zahlenwert 1.8 – 3 = –1.2.

Die ersten Zentralmomente einer Gaußschen Zufallsgröße mit Streuung $σ =$ 1/2 sind: $$\mu_2 = \frac{1}{4}, \hspace{0.4cm}\mu_4 = \frac{3}{16},\hspace{0.4cm}\mu_6 = \frac{15}{64}, \hspace{0.4cm}\mu_8 = \frac{105}{256}.$$ Alle Zentralmomente mit ungeradem Index sind identisch 0.

Mit dem folgenden Modul können Sie sich die Kenngrößen der Gaußverteilung anzeigen lassen: WDF, VTF und Momente spezieller Verteilungen

Erzeugung mittels Additionsmethode

Dieses einfache, auf dem zentralen Grenzwertsatz basierende Verfahren zur rechnertechnischen Generierung einer Gaußschen Zufallsgröße soll hier nur stichpunktartig skizziert werden:

(1) Man geht von (zwischen 0 und 1) gleichverteilten und statistisch voneinander unabhängigen Zufallsgrößen $u_i$ aus ⇒ Mittelwert 1/2, Varianz 1/12.

(2) Man bildet die Summe über $I$ Summanden, wobei $I$ hinreichend groß gewählt werden muss: $$s=\sum\limits_{i=1}^{I}u_i.$$ Nach dem zentralen Grenzwertsatz ist die Zufallsgröße $s$ mit guter Näherung gaußverteilt, wenn $I$ hinreichend groß gewählt wird. Für $I =$ 2 ergibt sich beispielsweise nur eine Dreieck–WDF (Faltung zweier Rechtecke).

(3) Der Mittelwert der Zufallsgröße $s$ beträgt somit $I/2$. Da die gleichverteilten Zufallsgrößen $u_i$ als statistisch voneinander unabhängig vorausgesetzt wurden, können auch ihre Varianzen addiert werden, so dass sich für die Varianz von $s$ der Wert $I/12$ ergibt.

(4) Soll eine gaußverteilte Zufallsgröße $x$ mit anderem Mittelwert $m_x$ und anderer Streuung $σ_x$ erzeugt werden, so muss noch folgende lineare Transformation durchgeführt werden: $$x=m_x+\frac{\sigma_x}{\sqrt{I/\rm 12}}\cdot[(\sum\limits_{\it i=\rm 1}^{\it I}u_i)-{I}/{\rm 2}].$$

(5) Mit dem Parameter $I =$ 12 vereinfacht sich die Generierungsvorschrift, was man insbesondere bei rechenzeitkritischen Anwendungen – z. B. bei einer Echtzeitsimulation – ausnutzen kann: $$x=m_x+\sigma_x\cdot[(\sum\limits_{i=\rm 1}^{12}\it u_i \rm )-\rm 6].$$ Die nach der Additionsmethode (mit Parameter $I$) approximierte Gaußsche Zufallsgröße liefert allerdings nur Werte in einem begrenzten Bereich um den Mittelwert $m_x$. Allgemein gilt: $$m_x-\sqrt{3 I}\cdot \sigma_x\le x \le m_x+\sqrt{3 I}\cdot \sigma_x.$$

Der Fehler gegenüber der theoretischen Gaußverteilung ist an diesen Grenzen am größten und wird für steigendes $I$ kleiner. Diesen Sachverhalt können Sie sich anhand eines Lernvideos verdeutlichen. Prinzip der Additionsmethode

Erzeugung mit dem Verfahren nach Box/Muller

Bei dieser Methode werden zwei statistisch voneinander unabhängige gaußverteilte Zufallsgrößen $x$ und $y$ aus den beiden zwischen 0 und 1 gleichverteilten und statistisch unabhängigen Zufallsgrößen $u$ und $υ$ durch nichtlineare Transformation erzeugt: $$x=m_x+\sigma_{x}\cdot\rm cos(2\it \pi u)\cdot\sqrt{\rm -2\cdot \rm ln(\it v)},$$ $$y=m_y+\sigma_{y}\cdot\rm sin(2\it \pi u)\cdot\sqrt{\rm -2\cdot \rm ln(\it v)}.$$

Das Verfahren nach Box und Muller – abgekürzt BM – kann wie folgt charakterisiert werden:

• Der theoretische Hintergrund für die Gültigkeit obiger Generierungsvorschriften basiert auf den Gesetzmäßigkeiten für zweidimensionale Zufallsgrößen (siehe Kapitel 4.1).
• Obige Gleichungen liefern sukszessive zwei Gaußwerte ohne statistische Bindungen untereinander. Diese Tatsache kann man zur Verkürzung der Simulationszeit nutzen, indem man bei jedem Funktionsaufruf ein Tupel $(x, y)$ von Gaußwerten generiert.
• Ein Vergleich der Rechenzeiten zeigt, dass – bei jeweils bestmöglicher Implementierung – das BM-Verfahren der Additionsmethode mit $I =$ 12 etwa um den Faktor 3 überlegen ist.
• Der Wertebereich ist beim BM-Verfahren weniger begrenzt als bei der Additionsmethode, so dass auch kleine Wahrscheinlichkeiten genauer simuliert werden. Aber auch mit dem BM-Verfahren lassen sich keine beliebig kleinen Fehlerwahrscheinlichkeiten simulieren.

Bei einem 32 Bit-Rechner ist die kleinste darstellbare Floatzahl $2^{–31} ≈ 0.466 · 10^{–9}.$ Für die nachfolgende Abschätzung setzen wir die Parameter $m_x = m_y =$ 0 und $σ_x = σ_y =$ 1 voraus.

• Der Maximalwert des Wurzelausdrucks in der Generierungsvorschrift des BM-Verfahrens kann somit nicht größer als ca. 6.55 werden und ist zudem äußerst unwahrscheinlich.
• Da sowohl die Cosinus- als auch die Sinusfunktion betragsmäßig auf 1 beschränkt ist, wäre das gleichzeitig der maximal mögliche Wert für die Zufallsgrößen $x$ und $y$.

Eine in [ES96] dokumentierte Simulation über eine Milliarde Abtastwerte hat aber gezeigt, dass das BM-Verfahren nur bis zu Fehlerwahrscheinlichkeiten von $10^{–5}$ die Q-Funktion sehr gut approximiert, dann aber der Kurvenverlauf steil abbricht. Der maximal auftretende Wert des Wurzelausdrucks war dabei nicht 6.55, sondern aufgrund der aktuellen Zufallsgrößen $u$ und $υ$ nur etwa 4.6, womit sich der schlagartige Abfall ab etwa $10^{–5}$ erklären lässt. Bei 64 Bit-Rechenoperationen kann dieses Verfahren natürlich noch deutlich verbessert werden.

Erzeugung mit dem Verfahren „Tabulated Inversion”

Bei diesem von P. Eck und G. Söder entwickelten Verfahren [ES96] wird wie folgt vorgegangen:

(1) Die Gauß–WDF wird in $J$ Intervalle mit gleichen Flächeninhalten – und dementsprechend unterschiedlicher Breite – aufgeteilt, wobei $J$ eine Zweierpotenz darstellt.

(2) Dem Intervall mit Index $j$ wird ein charakteristischer Wert $C_j$ zugeordnet. Somit genügt es, bei jedem Funktionsaufruf nur einen Integer-Zahlengenerator aufzurufen, der die ganzzahligen Werte $j = ±1, ... , ±J/2$ mit gleicher Wahrscheinlichkeit liefert und damit eines der $C_j$ auswählt.

(3) Wird $J$ hinreichend groß gewählt, z. B. $J = 2^{15} = 32768,$ so können die $C_j$ vereinfachend gleich den Intervallmittelwerten gesetzt werden. Diese Werte muss man nur einmal berechnen und können bereits vor der eigentlichen Simulation in einer Datei abgelegt werden.

(4) Die Randbereiche sind problematisch und müssen gesondert behandelt werden. Mittels nichtlinearer Transformation wird hierfür ein Floatwert gemäß den Ausläufern der Gauß-WDF bestimmt.

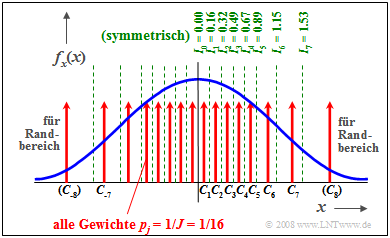
Die Skizze zeigt die WDF–Aufteilung für $J =$ 16 durch die Intervallgrenzen $I_{–7} ... I_7$. Diese Grenzen wurden so gewählt, dass jedes Intervall die gleiche Fläche $p_j = 1/J =$ 1/16 aufweist. Der charakteristische Wert $C_j$ eines jeden Intervalls liegt genau in der Mitte zwischen $I_{j–1}$ und $I_j$.

Man erzeugt nun eine gleichverteilte diskrete Zufallsgröße $k$ (hier zwischen 1 und 8) und dazu ein Vorzeichenbit. Bei negativem Vorzeichenbit und $k =$ 4 wird somit der Wert −(0.49+0.67)/2 ⇒ $C_4 =$ −0.58 ausgegeben. Bei $k =$ 8 tritt der Sonderfall ein, dass man den Zufallswert $C_8$ durch nichtlineare Transformation entsprechend den Ausläufern der Gaußkurve ermitteln muss.

Die Eigenschaften von „Tabulated Inversion” können wie folgt zusammengefasst werden:

• Diese Methode ist mit $J = 2^{15}$ bei vergleichbarer Simulationsgenauigkeit etwa um den Faktor 8 schneller als das BM-Verfahren.
• Nachteilig ist, dass nun die Überschreitungswahrscheinlichkeit Pr( $x > r$) in den inneren Bereichen nicht mehr kontinuierlich ist, sondern sich aufgrund der Diskretisierung eine Treppenkurve ergibt.
• Dieses Manko kann man durch ein größeres $J$ ausgleichen. Durch die Sonderbehandlung der Ränder eignet sich das Verfahren auch für sehr kleine Fehlerwahrscheinlichkeiten.