Aufgaben:Aufgabe 2.3: Sinusförmige Kennlinie

• Zurück zum Buch

Wie betrachten ein System mit Eingang $x(t)$ und Ausgang $y(t)$. Zur einfacheren Darstellung werden die Signale als dimensionslos betrachtet.

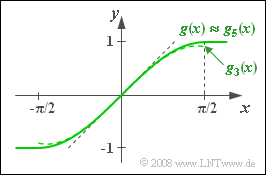
Der Zusammenhang zwischen dem Eingangssignal $x(t)$ und dem Ausgangssignal $y(t)$ ist im Bereich zwischen $-\pi/2$ und $+\pi/2$ durch die folgende Kennlinie gegeben. $$g(x) = \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \hspace{0.05cm}...$$

Der zweite Teil dieser Gleichung beschreibt dabei die Reihenentwicklung der Sinusfunktion. Als Näherungen für die nichtlineare Kennlinie werden in dieser Aufgabe verwendet: $$g_1(x) = x\hspace{0.05cm},$$ $$ g_3(x) = x- x^{3}\hspace{-0.1cm}/6\hspace{0.05cm},$$ $$g_5(x) = x- x^3\hspace{-0.1cm}/{6}+x^5\hspace{-0.1cm}/{120}\hspace{0.05cm}.$$

Es wird stets das Eingangssignal $x(t) = A \cdot \cos(\omega_0 \cdot t)$ vorausgesetzt, wobei für die (dimensionslose) Signalamplitude die Werte $A = 0.5$, $A = 1.0$ und $A = 1.5$ zu betrachten sind.

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|Nichtlineare Verzerrungen]].
• Die sich ergebenden Signalverläufe für $x(t)$ und $y(t)$ sind im Beispiel auf der Seite Beschreibung nichtlinearer Systeme grafisch dargestellt.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Alle hier abgefragten Leistungen beziehen sich auf den Widerstand $R = 1 \ \rm \Omega$ und haben somit die Einheit ${\rm V}^2$
• Als bekannt vorausgesetzt werden die folgenden trigonometrischen Beziehungen:

$$\cos^3(\alpha) = {3}/{4} \cdot \cos(\alpha) + {1}/{4} \cdot \cos(3\alpha) \hspace{0.05cm}, $$ $$ \cos^5(\alpha) = {10}/{16} \cdot \cos(\alpha) + {5}/{16} \cdot \cos(3\alpha) + {1}/{16} \cdot \cos(5\alpha)\hspace{0.05cm}.$$

Fragebogen

1

Welchen Klirrfaktor $K$ erhält man mit der Kennliniennäherung $g_1(x)$ unabhängig von der Amplitude $A$ des Eingangssignals?

$g_1(x)\hspace{-0.08cm}:\ \ K \ = $ $\ \%$

2

Berechnen Sie den Klirrfaktor $K$ für das Eingangssignal $x(t) = A \cdot \cos(\omega_0 \cdot t)$ und die Näherung $g_3(x)$. Welche Werte ergeben sich für $A = 0.5$ und $A = 1.0$?

$g_3(x),\ A = 0.5\hspace{-0.08cm}:\ \ K \ = $ $\ \%$

$g_3(x),\ A = 1.0\hspace{-0.08cm}:\ \ K \ = $ $\ \%$

3

Wie lautet der Klirrfaktor für $A = 1.0$ unter Berücksichtigung der Näherung $g_5(x)$?

$g_5(x),\ A = 1.0\hspace{-0.08cm}:\ \ K = $ $\ \%$

4

Welche der folgenden Aussagen treffen zu? Hierbei bezeichnet $K$ den Klirrfaktor der Sinusfunktion $g(x)$, während $K_{\rm g3}$ und $K_{\rm g5}$ auf den Näherungen $g_3(x)$ und $g_5(x)$ basieren.

	$K_{\rm g5}$ stellt im Allgemeinen eine bessere Näherung für $K$ dar als $K_{\rm g3}$.
	Für $A = 1.0$ ist $K_{\rm g3}$ kleiner als $K_{\rm g5}$.
	Für $A = 0.5$ wird $K_{\rm g3} \approx K_{\rm g5}$ gelten.

Musterlösung

Musterlösung

(1)  Die sehr ungenaue Näherung $g_1(x) = x$ ist linear in $x$ und führt deshalb auch nicht zu nichtlinearen Verzerrungen. Damit ergibt sich für den Klirrfaktor K = 0.

(2)  Das analytische Spektrum (nur positive Frequenzen) des Eingangssignals lautet: $$X_+(f) = A \cdot {\rm \delta}(f- f_0) .$$

Am Ausgang der nichtlinearen Kennlinie $g_3(x)$ liegt dann folgendes Signal an: $$y(t) = A \cdot {\rm cos}(\omega_0 t ) - \frac{A^3}{6} \cdot {\rm cos}^3(\omega_0 t )= A \cdot {\rm cos}(\omega_0 t ) - \frac{3}{4} \cdot \frac{A^3}{6} \cdot {\rm cos}(\omega_0 t )- \frac{1}{4} \cdot \frac{A^3}{6} \cdot {\rm cos}(3\omega_0 t ) = A_1 \cdot {\rm cos}(\omega_0 t ) + A_3 \cdot {\rm cos}(3\omega_0 t ).$$

Für die Koeffizienten $A_1$ und $A_3$ erhält man durch Koeffizientenvergleich: $$A_1 = A - {A^3}\hspace{-0.1cm}/{8}, \hspace{0.5cm}A_3 = - {A^3}\hspace{-0.1cm}/{24}.$$

Mit $A = 0.5$ ergibt sich $A_1 \approx 0.484$ und $A_3 \approx 0.005$. Somit lautet der Klirrfaktor: $$K = K_3 = \frac{|A_3|}{A_1}= {0.005}/{0.484} \hspace{0.15cm}\underline{ = 1.08\%}.$$

Anzumerken ist, dass bei der Näherung$g_3(x)$ nur der kubische Anteil $K_3$ des Klirrfaktors wirksam ist. Für $A = 1.0$und $A = 1.5$ ergeben sich folgende Zahlenwerte: $$A = 1.0: A_1 \approx 0.875, \hspace{0.2cm} A_3 \approx -0.041\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{K \approx 4.76\%},$$ $$A = 1.5: A_1 \approx 1.078, \hspace{0.2cm} A_3 \approx -0.140\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \hspace{0.15cm}{K \approx 13 \%}.$$

(3)  In ähnlicher Weise wie beim Unterpunkt 2) gilt nun

$$y(t) = A_1 \cdot {\rm cos}(\omega_0 t ) + A_3 \cdot {\rm cos}(3\omega_0 t )+ A_5 \cdot {\rm cos}(5\omega_0 t )$$

mit folgenden Koeffizienten:

$$A_1 = A - \frac{A^3}{8} + \frac{A^5}{192},\hspace{0.3cm} A_3 = - \frac{A^3}{24} + \frac{A^5}{384},\hspace{0.3cm} A_5 = \frac{A^5}{1920}.$$

Daraus ergeben sich mit A = 1 die Zahlenwerte:

$$A_1 \approx 1 -0.125 +0.005 = 0.880,\hspace{0.3cm} A_3 \approx -0.042 +0.003 = -0.039,\hspace{0.3cm} A_5 \approx 0.0005$$

$$\Rightarrow \hspace{0.3cm}K_3 = \frac{|A_3|}{A_1}= 0.0443,\hspace{0.3cm}K_5 = \frac{|A_5|}{A_1}= 0.0006 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K = \sqrt{K_3^2 + K_5^2} \hspace{0.15cm}\underline{\approx 4.45\%}.$$

(4)  Der Ansatz g₅(x) ist im gesamten Bereich eine bessere Näherung für die Sinusfunktion g(x) als die Näherung g₃(x). Deshalb ist der in der Teilaufgabe c) berechnete Wert K_c eine bessere Näherung für den tatsächlichen Klirrfaktor K als K_b – die erste Aussage ist somit richtig.

Dagegen ist die zweite Aussage falsch, wie schon die Berechnung gezeigt hat K_b = 4.76 % ist größer als K_c = 4.45 %. Der Grund hierfür ist, dass g₃(x) unterhalb von g₅(x) liegt und damit auch eine größere Abweichung vom linearen Verlauf vorliegt.

Für A = 0.5 wird K_c ≈ K_b gelten. Schon die Kennlinie auf der Angabenseite zeigt, dass für |x| ≤ 0.5 die beiden Funktionen g₃(x) und g₅(x) innerhalb der Zeichengenauigkeit nicht zu unterscheiden sind. Damit ergeben sich auch gleiche Klirrfaktoren. Richtig sind also die Lösungsvorschläge 1 und 3